2.15: Тест Венна валідність для негайних категоричних висновків

В останньому розділі ми ввели чотири категоричні форми. Ці форми наведені нижче.

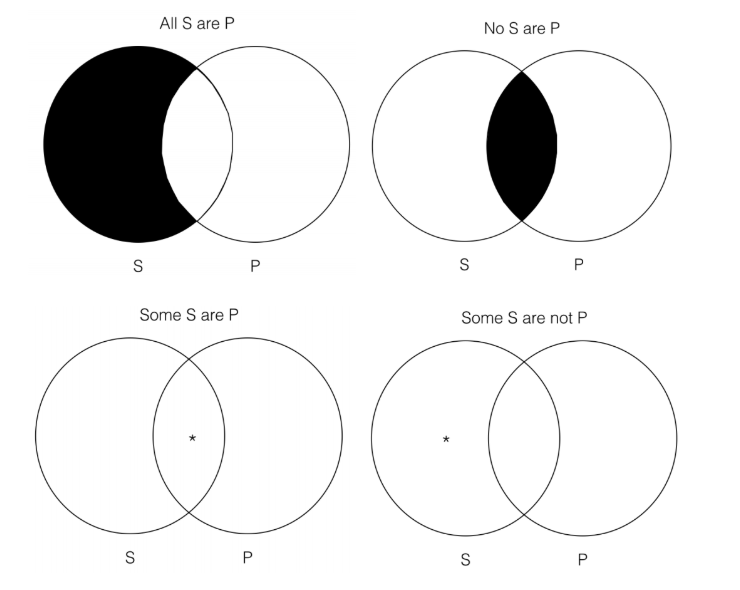
Ми можемо використовувати діаграми Венна для того, щоб визначити, чи є певні види аргументів дійсними чи недійсними. Одним з таких аргументів є те, що ми будемо називати «негайними категоричними висновками». Безпосередній категоричний висновок - це просто аргумент з однією передумовою і одним висновком. Наприклад:

1. Деякі ссавці є амфібіями.
2. Тому деякі земноводні речі є ссавцями.

Якщо побудувати діаграму Венна для передумови та іншу діаграму Венна для висновку, ми побачимо, що діаграми Венна ідентичні один одному.

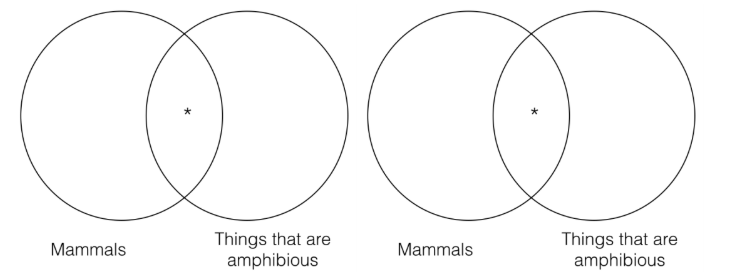
Тобто інформація, яка представлена в Венні для приміщення, - це точно така ж інформація, представлена в Венні для висновку. Цей аргумент проходить перевірку дійсності Венна, оскільки висновок Венна не містить додаткової інформації, яка вже не міститься в приміщенні Венна. Таким чином, даний аргумент є справедливим. Давайте тепер звернемося до прикладу недійсного аргументу.

1. Всі автомобілі - транспортні засоби.
2. Тому всі транспортні засоби є легковими.

Ось Венни для передумови та висновку відповідно:

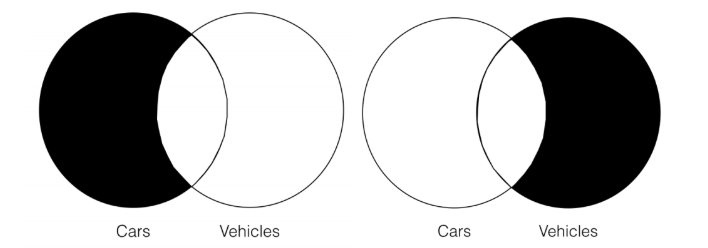
При цьому Венни явно не однакові. Що ще важливіше, ми бачимо, що висновок Венна (праворуч) містить додаткову інформацію, яка ще не міститься в приміщенні Венна. Зокрема, висновок Венна допускає, що а) в категорії «автомобіль» можуть бути речі, які не належать до категорії «транспортний засіб», і б) що в категорії «транспортний засіб» не може бути нічого, що також не входить до категорії «автомобіль». Це не інформація, яка міститься в приміщенні Venn, яка говорить про те, що а) немає нічого в категорії «автомобіль», що також не входить до категорії «транспортний засіб» і б), що в категорії «транспортний засіб» можуть бути речі, які не належать до категорії «автомобіль». Таким чином, цей аргумент не проходить тест Венна на валідність, оскільки є інформація, що міститься у висновку Венна, яка вже не міститься в передумові Венна. Таким чином, цей аргумент є недійсним. Тест Венна валідність є формальним методом, тому що ми можемо застосувати його, навіть якщо ми знаємо лише форму категоричних тверджень, але не знаємо, що представляють категорії, про які йдеться у твердженнях. Наприклад, ми можемо просто використовувати «S» і «P» для категорій - і ми явно не знаємо, що вони представляють. Наприклад:

1. Всі S є P
2. Ні P не є S

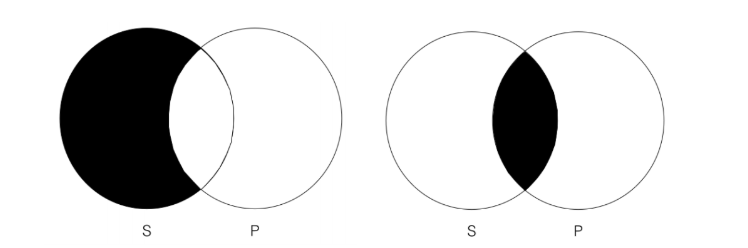
Висновок (праворуч) містить інформацію, яка не міститься в приміщенні (зліва). Зокрема, висновок Венн явно виключає, що є все, що є як у категорії «S», так і в категорії «P», тоді як передумова Венн дозволяє це так (але цього не вимагає). Таким чином, можна сказати, що цей аргумент не проходить тест Венна на валідність і, таким чином, є недійсним. Ми знаємо це, хоча ми поняття не маємо, що таке категорії «S» та «P». Це відмітка формального методу оцінки.

Вправа

Застосуйте тест Венна на валідність, щоб визначити, чи є наступні категоричні висновки дійсними чи недійсними.

1. Всі S є P; отже, всі P є S
2. Деякі S є P; отже, деякі P є S
3. Деякі S є P; тому деякі P не є S
4. Деякі S є P; отже, всі P є S
5. Ні S є P; отже, немає P є S
6. Ні P є S; отже, деякі S є P
7. Деякі S не є P; тому деякі P не є S
8. Всі S є P; тому деякі P не є S