2.17: Дійсність Венна для категоричних силогізмів
- Page ID
- 52014
Категоричний силогізм - це всього лише аргумент з двома передумами і висновком, де кожне твердження аргументу є категоричним твердженням. Як ми бачили, існує чотири різних типи (форми) категоричного висловлювання:
Всі S є P (універсальний ствердний)
Ні S є P (універсальний негативний)
Деякі S є P (особливо ствердно)
Деякі S не P (особливо негативні)
Таким чином, будь-який категоричний силогізм передумови і висновок будуть деякою сумішшю цих різних типів висловлювання. Аргумент, який я навів на початку розділу 2.13, був категоричним силогізмом. Тут, знову ж таки, є той аргумент:
1. Всі люди смертні
2. Всі смертні речі вмирають
3. Тому всі люди гинуть
Як ми бачимо зараз, коли ми дізналися чотири категоричні форми, кожне з тверджень у цьому силогізмі є «універсальним ствердним» твердженням форми, «всі S - це P». Давайте спочатку переведемо кожне твердження цього аргументу, щоб мати форму «всі S є P»:
1. Всі люди - це речі, які є смертними.
2. Все, що є смертним, - це речі, які вмирають.
3. Всі люди - це речі, які вмирають.
При визначенні обґрунтованості категоричних силогізмів ми повинні побудувати три категорії діаграму Венна для приміщень і двокатегорійну діаграму Венна для висновку. Ось як виглядає три категорії Венн для приміщень:
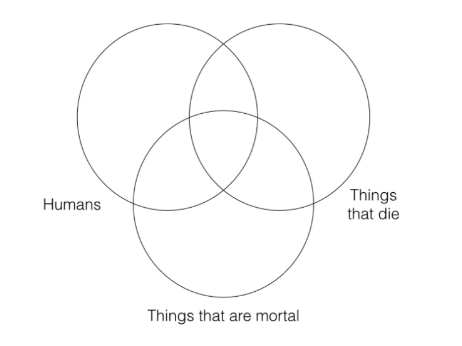
Нам потрібна три категорії Венн для приміщень, оскільки два приміщення відносяться до трьох різних категорій. Спосіб побудови Венна - це коло, який представляє категорію «S» висновку (тобто категорію «люди») зліва, коло, що представляє категорію «Р» висновку (тобто категорію «речі, які вмирають») праворуч, а решта категорії («речі, які смертні») ) посередині, як я зробив вище. Побудова трьох категорій Венн таким чином дозволить вам легко визначити, чи є аргумент дійсним.
Наступне, що ми повинні зробити, це представити інформацію з перших двох приміщень у нашій три категорії Венн. Ми почнемо з першої передумови, яка говорить: «всі люди - це речі, які є смертними». Це означає, що ми повинні затінювати все, що є в категорії «людина», але це не в категорії «смертні речі», як це:
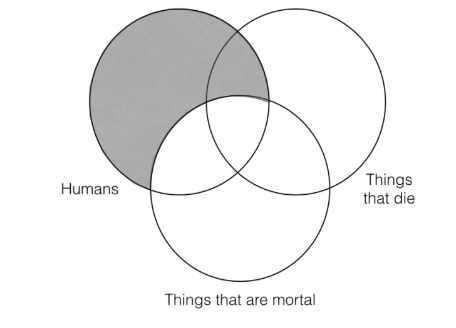
Наступне, що нам потрібно зробити, це заповнити інформацію для другої передумови, все, що є смертними, - це речі, які вмирають. Це означає, що немає нічого, що знаходиться в категорії «речі, які смертні», але це не в категорії «речі, які вмирають». Тож ми повинні затінювати всі частини категорії «речі, які смертні», брехня поза категорією «речі, які вмирають», як це:
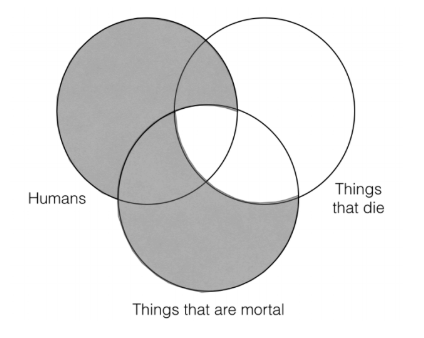
Наступне, що нам потрібно зробити, це побудувати дві категорії Венн для висновку, а потім порівняти інформацію, представлену трьома категоріями Венн для приміщень, з двома категоріями Венн для висновку.
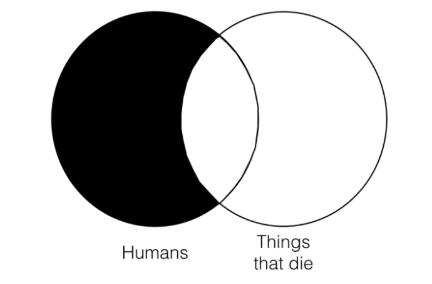
Висновок являє собою інформацію про те, що в категорії «люди» немає нічого, що не є також у категорії «речі, які вмирають». Це також дозволяє, що є речі, які вмирають, але це не люди. Приміщення Венна також включає цю саму інформацію, оскільки кожна частина категорії «люди», яка знаходиться поза категорією «речі, які вмирають», затінена. Таким чином, цей аргумент проходить тест Венна на валідність і, таким чином, є дійсним, оскільки у висновку Венна немає інформації, яка також не представлена в передумові Венна. Зверніть увагу, що не має значення, що приміщення Венна містить більше інформації, ніж висновок Венна. Це слід очікувати, оскільки приміщення Венн представляє цілу іншу категорію, що висновок Венна не є. Те, що не допустимо (і, таким чином, змусить аргумент провалитися тест Венна на валідність), якщо висновок Венна містив інформацію, яка ще не містилася в приміщенні Венна. Однак, оскільки цей аргумент цього не робить, він є дійсним.
Спробуємо ще один.
1. Всі педіатри лікарі
2. Всі педіатри люблять дітей
3. Тому всім лікарям подобаються діти.
Першим кроком є визначення трьох категорій, про які йдеться в цьому категоричному силогізмі. Ними є:
Педіатри
Лікарі
Речі, які подобаються дітям
Наступним кроком є заповнення трьох категорій Венн для приміщення і дві категорії Венн для висновку.

Цей аргумент не проходить перевірку дійсності Венна, оскільки є інформація, що міститься у висновку Венна, яка не міститься в передумові Венна. Зокрема, висновок говорить про те, що в категорії «лікарі» немає нічого, що знаходиться поза категорією «речі, які подобаються дітям». Однак приміщення не представляють цієї інформації, оскільки розділ категорії «лікарі», який лежить поза перетином категорії «речі, які люблять дітей», є незатіненим, таким чином представляючи, що там можуть бути речі.
Іноді при заповненні конкретної заяви по трьом категоріям для приміщення ви зіткнетеся з проблемою, яка вимагає іншої умовності, щоб точно представляти інформацію в Венн. Ось приклад, де це відбувається:
1. Деякі ссавці - ведмеді
2. Деякі двоногі істоти - ссавці
3. Тому деякі двоногі істоти - ведмеді.
Існує три категорії, про які йдеться в цьому категоричному силогізмі:
Ссавці
Ведмеді
Двоногі істоти
Як завжди, ліворуч від наших трьох категорій Венна ми поставимо термін «S» висновку, справа - термін «P», а решта - посередині, наступним чином:
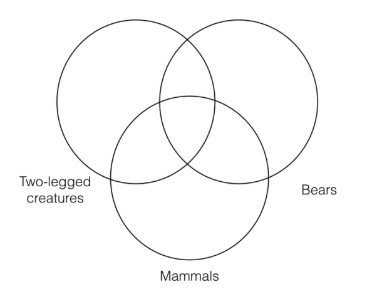
Тепер нам потрібно зобразити першу передумову, а значить, потрібно поставити зірочку на перетині категорій «ссавці» і «ведмеді». Однак тут у нас є вибір, який потрібно зробити. Оскільки перетин категорій «ведмеді» та «ссавці» містить розділ, який знаходиться поза категорією «двоногі істоти», і розділ, який знаходиться всередині категорії «двоногі істоти», ми повинні вибирати між представленням конкретного як частина категорії «двоногі істоти» чи ні.
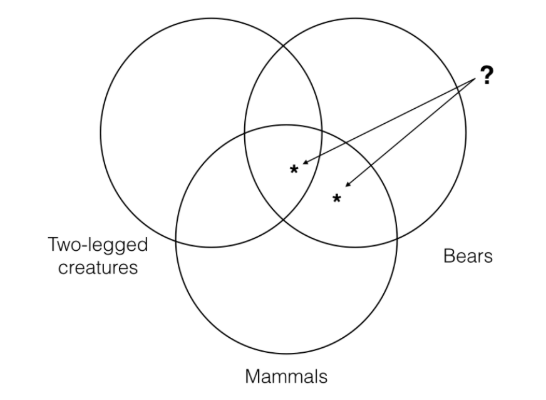
Але жодне з них не може бути правильним, оскільки перша передумова взагалі нічого не говорить про те, чи є річ, яка і ведмідь, і ссавець, двонога! Таким чином, щоб точно представити інформацію, що міститься в цій передумові, ми повинні прийняти нову конвенцію. Ця конвенція говорить, що коли ми стикаємося з ситуацією, коли ми повинні представляти певну частину нашої три категорії Венна, але передумова нічого не говорить про конкретну категорію, то ми повинні поставити зірочку на рядок цієї категорії, як я зробив нижче. Коли ми це зробимо, це буде представляти, що конкретний не знаходиться ні всередині категорії, ні поза категорією.
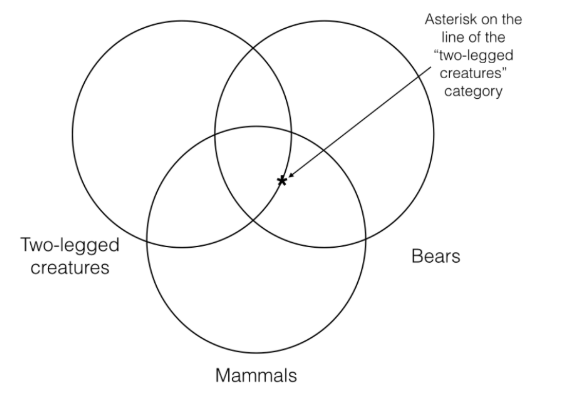
Ми повинні зробити те саме для другої передумови, оскільки ми стикаємося з тією ж проблемою. Таким чином, ставлячи зірочку на перетині категорій «двоногі істоти» і «ссавці», ми не можемо ставити зірочку ні всередині, ні зовні категорії «ведмеді». Замість цього ми повинні поставити зірочку на рядок категорії «ведмеді». Таким чином, використовуючи цю конвенцію, ми можемо представити передумову Венна та висновок Венна наступним чином:
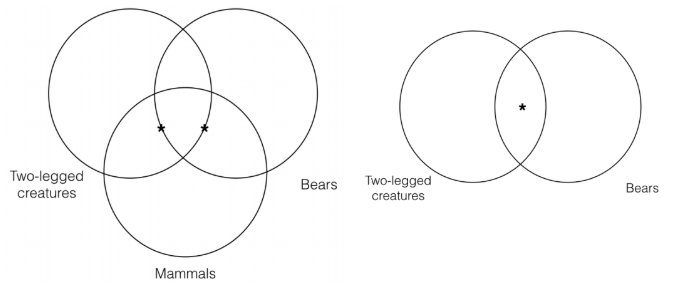
Маючи на увазі конвенцію, яку ми щойно ввели, ми бачимо, що цей аргумент не проходить тест Венна на валідність і, таким чином, є недійсним. Причина полягає в тому, що висновок Венн чітко представляє індивіда на перетині категорій «двоногих істот» та «ведмедів», тоді як приміщення Венн не містить такої інформації. Таким чином, висновок Венна містить інформацію, яка не міститься в передумові Венна, а значить аргумент недійсний.
Ми закриємо цей розділ останнім прикладом, який проілюструє важливу стратегію. Стратегія полягає в тому, що ми завжди повинні відображати універсальні твердження перед відображенням певних тверджень. Ось категоричний силогізм, який ілюструє цей момент. Цього разу я збираюся перейти на просто використання великих літер S, P і M для представлення категорій. Нагадаємо, що ми можемо це зробити, оскільки тест Венна валідність є формальним методом оцінки, де нам не потрібно насправді розуміти, що представляють категорії у світі, щоб визначити, чи є аргумент дійсним.
1. Деякі S є M
2. Всі М є P
3. ly Деякі S є P
Якщо ми думаємо про відображення першої передумови на нашу три категорії Венна, здається, що нам доведеться використовувати щойно введену нами конвенцію, оскільки перша передумова - це конкретне категоричне твердження, яке згадує лише категорії S і M і нічого про категорію P:
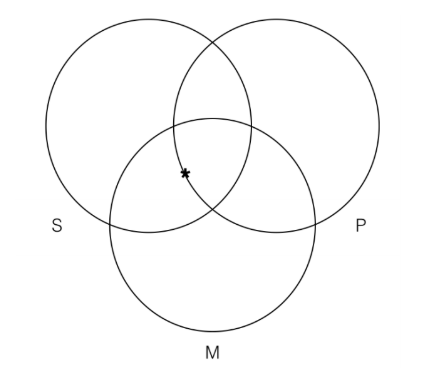
Однак, як виявляється, ми не повинні використовувати цю конвенцію, тому що коли ми зіставляємо передумова 2, яка є універсальним твердженням, це очищає, куди має йти зірочка:
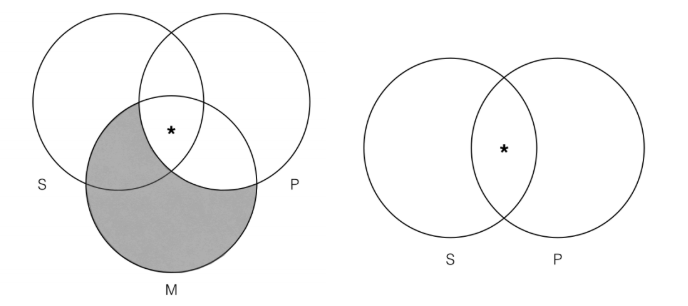
Ми бачимо, що після того, як ми зіставили універсальне твердження на приміщення Венна (ліворуч), є лише один розділ, де зірочка може йти, яка знаходиться на перетині S і M. Причина полягає в тому, що як тільки ми зіставили «всі M є P» передумова, і таким чином затінювали будь-яку частину категорії М, що знаходиться поза категорією P, ми знаємо, що зірочка не може належати до категорії M, враховуючи, що вона повинна бути всередині категорії P. Коли ми застосовуємо тест Венна на валідність до вищезазначеного аргументу, ми бачимо, що він дійсний, оскільки висновок Венна не містить жодної інформації, яка вже не міститься в приміщенні Венна. Висновок просто говорить про те, що є щось, що є і S, і P, і ця інформація вже представлена в нашому приміщенні Венн. Таким чином, аргумент є справедливим. Сенс стратегії тут полягає в тому, що ми завжди повинні відображати наші універсальні твердження на три категорії Венни, перш ніж відображати наші конкретні твердження. Причина в тому, що універсал може визначити, як ми відображаємо наші конкретні твердження (але не навпаки).
Вправа
Використовуйте тест Венна на валідність, щоб визначити, чи є наступні силогізми дійсними чи недійсними.
1. Все М - це P
Все M є S
, All S є P
2. Все P - це М
Все M є S,
All S - це P
3. Все M є P
Деякі M є S
, Деякі S є P
4. Всі P є M
Деякі M є S
, Деякі S є P
5. Всі P є M
Деякі S є M
⟩ Деякі S є P
6. Всі P є M
Деякі S не M
⟩ Деякі S не P
7. Все M є P
Деякі S не M
⟩ Деякі S не P
8. Все M є P
Деякі M не S
⟩ Деякі S не P
9. Ні M є P
Деякі S є
M ⟩ Деякі S не P
10. Ні P є M
Деякі S є
M ⟩ Деякі S не P
11. Ні P є M
Деякі S не M
⟩ Деякі S не P
12. Ні M є P
Деякі S не M
⟩ Деякі S не P
13. Ні P є M
Деякі M не S
⟩ Деякі S не P
14. Ні Р не M
Ні М є S,
No S є P
15. Ні Р - це М
Все М є S
, No S є P
16. Ні Р - це М
Все S є M
, No S є P
17. Всі P є М
Ні S є М,
No S є P
18. Всі М є P
No S є М
, No S є P
19. Деякі M є P
Деякі M не S
⟩ Деякі S не P
20. Деякі P є M
Деякі S не M
⟩ Деякі S є P
