2.11: Докази та вісім дійсних форм висновку
Хоча таблиці істинності є нашим єдиним формальним методом вирішення того, чи є аргумент дійсним чи недійсним у логіці пропозицій, існує ще один формальний метод доведення того, що аргумент є дійсним: метод доказування. Хоча ви не можете побудувати доказ, щоб показати, що аргумент є недійсним, ви можете побудувати докази, щоб показати, що аргумент є дійсним. Причина докази є корисними, полягає в тому, що вони дозволяють нам показати, що певні аргументи є дійсними набагато ефективніше, ніж таблиці істинності. Наприклад, розглянемо наступний аргумент:
1. (R v S) taLi (Т taLK)
2. ~К
3. R v S /∴ ~Т
(Примітка: у цьому розділі я буду писати висновок аргументу праворуч від останнього приміщення - в даному випадку передумова 3. Як і раніше, висновок, який ми намагаємося вивести, позначається знаком «отже», «⋅».) Ми могли б спробувати довести, що цей аргумент є дійсним з таблицею істинності, але таблиця істини буде 16 рядків довжиною, тому що є чотири різні атомні пропозиції, які відбуваються в цьому аргументі, R, S, T і K. Якби було 5 або 6 різних атомних пропозицій, таблиця істини буде 32 або 64 рядків довжиною! Однак, як ми незабаром побачимо, ми також можемо довести, що цей аргумент є дійсним лише двома додатковими рядками. Це здається набагато ефективнішим способом встановлення того, що цей аргумент є дійсним. Ми зробимо це трохи пізніше - після того, як ми ввели 8 дійсних форм висновку, які вам знадобляться для того, щоб робити докази. Кожен рядок доказу буде виправданий посиланням на одне з цих правил, причому останній рядок доказу - висновок, який ми намагаємося в кінцевому підсумку встановити. Я введу 8 дійсних форм висновку в групах, починаючи з правил, які використовують підкову та заперечення.
Перша з 8 форм висновку - «modus ponens», що є латинською мовою «спосіб, який підтверджує». Modus ponens має наступну форму:
1. р
aLi q 2. р
3.
Те, що ця форма говорить, словами, є те, що якщо ми стверджували умовний оператор (p aLit q), і ми також стверджували попередник цього умовного оператора (p), то ми маємо право зробити висновок наслідок цього умовного оператора (q). Наприклад, якщо я стверджував умовне, «якщо йде дощ, то земля мокра», і я також стверджував, що «йде дощ» (попередник цього умовного), то я (або хтось інший, на це питання) маю право стверджувати наслідок умовного, «земля мокра».
Як і у випадку з будь-якими дійсними формами висновку в цьому розділі, ми можемо довести, що modus ponens є дійсним шляхом побудови таблиці істинності. Як ви бачите з таблиці істинності нижче, ця форма аргументу проходить перевірку достовірності таблиці істинності (оскільки немає рядка таблиці істинності, на якій всі умови є істинними, і все ж висновок помилковий).
| р | q | р aLi q | р | q |
| Т | Т | Т | Т | Т |
| Т | F | F | Т | F |
| F | Т | Т | F | Т |
| F | F | Т | F | F |
Таким чином, будь-який аргумент, який має таку ж форму, є справедливим. Наприклад, такий же вигляд має такий аргумент (modus ponens):
1. (A ⋅ B) TL C
2. (A ⋅ Б)
3.
У цьому аргументі ми можемо стверджувати C відповідно до правила, modus ponens. Це так, навіть якщо попередник умовного сам по собі складний (тобто це кон'юнкція). Це не має значення. Перша передумова все ще є умовним твердженням (оскільки підкова є головним оператором), а друга передумова є попередником цього умовного оператора. Правило modus ponens говорить, що якщо у нас є стільки, ми маємо право зробити висновок про наслідок умовного.
Насправді ми можемо використовувати modus ponens у першому аргументі цього розділу:
1. (R v S) taLi (Т taLK)
2. ~К
3. R v S /⋅ ~Т
4. T = K Модус Поненс, лінії 1, 3
Те, що я зробив тут, я написав дійсну форму висновку (або правило), яка виправдовує лінію, яку я отримую, а також рядки, до яких застосовується це правило, праворуч від нового рядка доказу, що я отримую. Тут я вивів «T aCill K» з рядків 1 та 3 аргументу за модусом ponens. Зверніть увагу, що рядок 1 є умовним оператором, а рядок 3 є попередником цього умовного оператора. Цей доказ ще не закінчений, оскільки ми ще не зробили висновку, який ми намагаємося вивести, а саме «~T». Нам потрібно інше правило, щоб вивести те, яке ми введемо далі.
Наступна форма висновку називається «modus tollens», що є латинською мовою «спосіб, який заперечує». Модус толленс має наступну форму:
1. р
. ~q
3,0 ~ р
Те, що ця форма говорить, словами, є те, що якщо ми стверджували умовну заяву (p aLit q) і ми також стверджували заперечений наслідок цього умовного (~q), то ми маємо право зробити висновок заперечений попередник цього умовного оператора (~p). Наприклад, якщо я стверджував умовне, «якщо йде дощ, то земля мокра», і я також стверджував, що «земля не мокра» (заперечений наслідок цього умовного), то я маю право стверджувати заперечений попередник умовного, «не йде дощ». Важливо бачити, що будь-який аргумент, який має таку ж форму, є вагомим аргументом. Наприклад, наступний аргумент також є аргументом з такою ж формою:
1. С taLi (Е в Ф)
2. ~ (Е в Ф)
3.17 ~С
У цьому аргументі ми можемо стверджувати ~C відповідно до правила, modus tollens. Це так, навіть якщо наслідок умовного є самим складним (тобто це диз'юнкція). Це не має значення. Перша передумова все ще є умовним твердженням (оскільки підкова є головним оператором), а друга передумова є запереченим наслідком цього умовного оператора. Правило modus tollens говорить, що якщо у нас є стільки, ми маємо право зробити висновок про заперечений попередник умовного.
Ми можемо використовувати modus tollens, щоб завершити доказ, який ми розпочали вище:
1. (R v S) taLi (Т taLK)
2. ~К
3. R v S /⋅ ~Т
4. T = K Модус Поненс, лінії 1, 3,
5. ~T Модуль плати, лінії 2, 4
Зверніть увагу, що останній рядок доказу - це висновок, який ми повинні вивести, і що кожне твердження, яке я вивів (тобто рядки 4 і 5) має правило праворуч. Це правило, яке цитується, є правилом, яке виправдовує твердження, яке виводиться, а наведені рядки - це попередні рядки доказу, де ми можемо побачити, що правило застосовується. Це те, що називається доказом. Доказом є ряд тверджень, починаючи з приміщення і закінчуючи висновком, де кожне додаткове твердження після приміщення виводиться з якогось попереднього рядка (ів) доказу з використанням однієї з дійсних форм висновку. Ми будемо практикувати це ще трохи у вправі в кінці цього розділу.
Наступна форма висновку називається «гіпотетичний силогізм». Це те, що стародавні філософи називали «ланцюговим аргументом», і це повинно бути очевидно, чому через мить. Ось така форма правила:
1. р
taLi q 2. q taLi р
3.
Як бачите, висновок цього аргументу пов'язує p і r разом в умовний оператор. Ми могли б продовжувати додавати умовні умови, такі як «r taLi s» та «s», і висновки будуть настільки ж дійсними. І якщо ми вибудували їх усі, як я маю нижче, ви можете зрозуміти, чому стародавні філософи називали цю вагому форму аргументу «ланцюговим аргументом»:
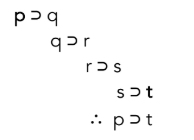
Зверніть увагу, як наслідок кожного попереднього умовного оператора зв'язується з попередником наступного умовного оператора таким чином, щоб створити ланцюжок. Ланцюжок може бути стільки, скільки нам сподобалося, але правило, яке ми наведемо в наших доказах, з'єднує лише два різних умовних оператора разом. Як і раніше, важливо усвідомлювати, що будь-який аргумент з такою ж формою є вагомим аргументом. Наприклад,
1. (А в Б) TL ~ D
2. ~D Це C
3. ⋅ (А в Б), TL C
Зверніть увагу, що наслідком першої передумови та попередня частина другої передумови є точно таким же терміном, «~D». Саме це дозволяє нам «зв'язати» попередню частину першої передумови та наслідок другої передумови разом у «ланцюжок», щоб зробити висновок. Вміти розпізнавати форми цих висновків є важливим навиком, що вам доведеться стати досвідченим, щоб зробити докази.
Наступні чотири форми висновку ми введемо використовувати кон'юнкцію, диз'юнкцію та заперечення по-різному. Почнемо з правила під назвою «спрощення», яке має наступний вигляд:
1. р ⋅ q
2.
Те, що це правило говорить словами, полягає в тому, що якщо ми затвердили сполучник, то ми маємо право зробити висновок або один із кон'юнктів. Це правило, яке я ввів в першому розділі цієї глави. Це досить «очевидне» правило - настільки очевидне, насправді, що ми можемо навіть задатися питанням, чому ми повинні це констатувати. Однак кожна форма висновку, яку ми введемо в цьому розділі, повинна бути очевидною - це сенс називати їх основними формами висновку. Вони є одними з найпростіших форм висновку, дійсність яких повинна бути прозоро очевидною. Ідея доказу полягає в тому, що хоча висновок, який робиться в аргументі, не є очевидним, ми можемо розірвати цей висновок кроками, кожен з яких очевидний. Таким чином, очевидні висновки в кінцевому підсумку виправдовують неочевидний висновок, зроблений в аргументі. Таким чином, ці очевидні висновки функціонують як правила, які ми використовуємо для обґрунтування кожного кроку доказу. Спрощення - яскравий приклад одного з найбільш очевидних правил.
Як і раніше, важливо усвідомити, що будь-який висновок, який має ту ж форму, що і спрощення, є дійсним висновком. Наприклад,
1. (А v B) ⋅ ~ (С ⋅ D)
2. ∴ (А v B)
є дійсним висновком, оскільки він має ту саму форму, що і спрощення. Тобто, рядок 1 є сполучником (оскільки точка є головним оператором речення), а рядок 2 - це висновок одного з сполучників цього сполучника в рядку 1. (Просто подумайте про «A v B» як «р», а «~ (C ⋅ D)» як «q».)
Наступне правило, яке ми введемо, називається «кон'юнкція» і схоже на зворотне спрощення. (Не плутайте правило, яке називається кон'юнкцією, з типом складної пропозиції, яка називається кон'юнкцією.) Кон'юнкція має наступну форму:
1. р
2. q
3. ⋅ р ⋅ q
Те, що це правило говорить словами, полягає в тому, що якщо ви стверджували дві різні пропозиції, то ви маєте право стверджувати поєднання цих двох пропозицій. Як і раніше, важливо розуміти, що будь-який висновок, який має ту ж форму, що і кон'юнкція, є дійсним висновком. Наприклад,
1. A | B
2. C v D
3. ⋅ (A Al B) ⋅ (С v D)
є дійсним висновком, оскільки він має ту саму форму, що і кон'юнкція. Ми просто поєднуємо дві пропозиції разом; неважливо, чи є ці пропозиції атомними чи складними. У цьому випадку, звичайно, пропозиції, які ми об'єднуємо разом, є складними, але до тих пір, поки ці пропозиції вже були затверджені як передумови в аргументі (або отримані деякою іншою дійсною формою висновку), ми можемо об'єднати їх разом у сполучник.
Наступна форма висновку, яку ми введемо, називається «диз'юнктивний силогізм» і вона має наступну форму:
1. р в q
2. ~p
3.17 q
На словах, це правило говорить, що якщо ми стверджували диз'юнкцію і ми стверджували заперечення одного з диз'юнктів, то ми маємо право стверджувати інший диз'юнкт. Як тільки ви подумаєте про це, цей висновок повинен бути досить очевидним. Якщо ми сприймаємо як належне істину припущень - що або p, або q вірно; і що р не є істинним, то слід слідувати, що q є істинним для того, щоб оригінальна диз'юнкція була правдою. (Пам'ятайте, що ми повинні припустити, що умови є істинними при оцінці того, чи є аргумент дійсним.) Якщо я стверджую, що це правда, що або Боб, або Лінда вкрали алмаз, і я стверджую, що Боб не вкрав алмаз, то це повинно слідувати, що це зробила Лінда. Це диз'юнктивний силогізм. Як і раніше, будь-який аргумент, який має таку ж форму, є дійсним аргументом. Наприклад,
1. ~А v (B ⋅ С)
2. ~~A
3,7 Б ⋅ С
є дійсним висновком, оскільки він має ту ж форму, що і диз'юнктивний силогізм. Перша передумова - це диз'юнкція (оскільки клин є головним оператором), друга передумова - це просто заперечення лівого диз'юнкта, «~A», а висновок - правий диз'юнкт початкової диз'юнкції. Це може допомогти вам побачити форму аргументу, якщо ви розглядаєте «~A» як p, а «B ⋅ C» як q, також зверніть увагу, що друга передумова містить подвійне заперечення. Ваш викладач англійської може сказати вам ніколи не використовувати подвійні негативи, але що стосується логіки, немає абсолютно нічого поганого в подвійному запереченні. У цьому випадку наш лівий диз'юнкт у приміщенні 1 сам по собі є запереченням, тоді як передумова 2 - це просто заперечення цього лівого диз'юнкту.
Наступне правило, яке ми введемо, називається «додавання». Це не зовсім таке «очевидне» правило, як ті, які ми ввели вище. Однак, як тільки ви зрозумієте умови, при яких диз'юнкція істинна, то повинно бути очевидно, чому ця форма висновку дійсна. Додаток має наступний вигляд:
1. р
2. ⋅ р v q
Те, що це правило говорить на словах, полягає в тому, що якщо ми стверджували якусь пропозицію, р, то ми маємо право стверджувати диз'юнкцію цієї пропозиції p та будь-якої іншої пропозиції q, яку ми хочемо. Ось просте обгрунтування правила. Якщо ми знаємо, що р істинно, і диз'юнкція істинна, якщо принаймні один з диз'юнктів є істинним, то ми знаємо, що диз'юнкція р v q є істинним, навіть якщо ми не знаємо, чи є q істинним чи хибним. Чому? Тому що не має значення, чи q є істинним чи хибним, оскільки ми вже знаємо, що р є істинним. Найважче зрозуміти про це правило, чому ми коли-небудь хотіли б використовувати його. Найкраща відповідь, яку я можу дати вам за це зараз, - це те, що вона може допомогти нам, роблячи докази. 3
Як і раніше, чи важливо усвідомлювати, що будь-який аргумент, який має таку ж форму, є вагомим аргументом. Наприклад,
1. А v B
2.7% (А v B) v (~C v D)
є дійсним висновком, оскільки він має ту саму форму, що і додавання. Перша передумова стверджує твердження (яке в даному випадку є складним - диз'юнкція), а висновок є диз'юнкцією цього твердження та деякого іншого твердження. У цьому випадку, що інше твердження саме по собі складне (диз'юнкція). Але аргумент або висновок можуть мати однакову форму, незалежно від того, чи є компоненти цих речень атомними чи складними. Це важливий урок, який я намагався просвердлити в цьому розділі.
Заключна з наших 8 дійсних форм висновку називається «конструктивною дилемою» і є найскладнішою з них усіх. Можливо, найбільш корисно ввести його на прикладі. Припустимо, я аргументував таким чином:
Вбивця знаходиться або на горищі, або в підвалі. Якщо вбивця на горищі значить він вище мене. Якщо вбивця в підвалі, то його нижче мене. Тому вбивцею є або _________________, або _________________.
Чи можете ви заповнити пропуски фразами, які б зробили цей аргумент дійсним? Я здогадуюся, що ви можете. Вона повинна бути досить очевидною. Висновок аргументу наступний:
Вбивця або вище мене, або нижче мене.
Те, що цей аргумент є дійсним, має бути очевидним (чи можете ви уявити собі сценарій, коли всі приміщення вірні і все ж висновок помилковий?). Що може бути не настільки очевидним, так це форма, яку має цей аргумент. Тим не менш, ви повинні бути в змозі визначити цю форму, якщо ви використовуєте інструменти, які ви вивчили досі. Перша передумова - диз'юнкція. Друга передумова - умовне твердження, попередник якого є лівим диз'юнктом диз'юнкції в першій передумові. І третя передумова - це умовне твердження, попередник якого є правильним диз'юнктом диз'юнкції в першій передумові. Висновок - диз'юнкція наслідків умовних в приміщеннях 2 і 3. Ось така форма висновку з використанням символів:
1. р v q
2. р
taLi р 3. q taLi s
4.
Зараз ми представили кожну з 8 форм висновку. У наступному розділі я проведу вас через деякі основні докази, які використовують ці 8 правил.
Вправа
Заповніть пропуски дійсною формою висновку, яка використовується, та рядками, з яких випливає висновок. Примітка: висновок пишеться праворуч від останньої передумови, слідуючи символам «/emy».
Приклад 1:
1. М:: ~ N
2. М
3. Н = N /emy ~H
4. ~N Модус поненс, 1, 2,
5. ~H Модуль живлення, 3, 4
Приклад 2:
1. А в Б
2. C | D
3. A: C
4. ~Д /⋅ Б
5. A | D Гіпотетичний силогізм, 3, 2,
6. ~A Модуль управління, 5, 4,
7. B Диз'юнктивний силогізм, 1, 6
# 1
1. A ⋅ С /⋅ (А в Е) ⋅ (С v D)
2. A _________________
3. С _________________
4. А в Е _________________
5. С в Д _________________
6. (А в Е) ⋅ (С v D) ______________
# 2
1. A (B | D)
2. ~Д
3. Д в А /⋅ ~Б
4. A _________________
5. Б, Д _________________
6. ~Б _________________
# 3
1. A TL ~B
2. А в С
3. ~~B ⋅ Д /⋅ C
4. ~В _________________
5. ~А _________________
6. C _________________
#4
1. A | B
2. A ⋅ ~Д
3. B ∞ С /⋅ C ⋅ ~Д
4. A _________________
5. A: C _________________
6. С _________________
7. ~Д _________________
8. C ⋅ ~Д _________________
#5
1. С
2. A | B
3. C | D
4. D AL/E /⋅ Е v B
5. C | Е _________________
6. С в А _________________
7. Е в Б _________________
#6
1. (А в М) | R
2. (Л taLR) ⋅ ~ R
3. ~ (С ⋅ Г) v (A v M) /⋅ ~ (С ⋅ D)
4. ~Р _______________
5. ~ (А в М) _______________
6. ~ (C ⋅ D) _______________
#7
1. (H ⋅ К) TL L
2. ~R ⋅ К
3. К taLi (Н в Р) /⋅ Л
4. К _________________
5. Н в Р _________________
6. ~Р _________________
7. Н _________________
8. Н ⋅ К _________________
9. Л _________________
#8
1. C | B
2. ~Д ⋅ ~Б
3. (A, TL (B | C)) v D
4. А в С /⋅ Б | С
5. ~Д _________________
6. A (B TL C) _____________
7. ~Б _________________
8. ~С __________________
9. А __________________
10. Б til С __________________
11. ~Б __________________
12. (B | C) v B __________________
3 Краща відповідь полягає в тому, що нам потрібно це правило для того, щоб зробити цей набір правил, які я представляю звуком, повний набір правил. Тобто, без нього були б аргументи, які є дійсними, але які ми не можемо показати дійсні, використовуючи цей набір правил. У більш просунутих областях логіки, таких як металогіка, логіки намагаються довести речі про певну систему логіки, наприклад, довести, що система є здоровою і повною.
