B: Математичні основи
- Page ID
- 4000
Квадрати та інші повноваження
Показник, або сила, - це математичне скорочення для повторних множень. Наприклад, показник «2» означає помножити базу для цього показника на себе (у прикладі тут база - «5»):
\[5^2=5×5=25\]
Показник дорівнює «2», а база - число «5». Цей вираз (множення числа на себе) ще називають квадратом. Будь-яке число, підняте до ступеня 2, зводиться в квадрат. Будь-яке число, підняте до ступеня 3, кубічно:
\[5^3=5×5×5=125\]
Число, підняте до четвертої влади, дорівнює тому числу, помноженому на себе чотири рази, і так далі для вищих сил. Загалом:
\[n^x=n×n^{x−1}\]
Обчислення відсотків
Відсоток - це спосіб вираження дробової кількості чогось за допомогою цілого, розділеного на 100 частин. Відсоток - це коефіцієнт, знаменник якого дорівнює 100. Ми використовуємо символ відсотка,%, щоб показати відсоток. Таким чином, 25% означає співвідношення\(\frac{25}{100}\), 3% означає співвідношення\(\frac{3}{100}\), а 100% відсотків означає\(\frac{100}{100}\), або ціле.
Перетворення відсотків
Відсоток можна перетворити в дріб, написавши значення відсотка у вигляді дробу зі знаменником 100 і спростивши дріб, якщо це можливо.
\[25\%=\dfrac{25}{100}=\dfrac{1}{4}\]
Відсоток можна перетворити в десятковий, написавши значення відсотка у вигляді дробу зі знаменником 100 і розділивши чисельник на знаменник.
\[10\%=\dfrac{10}{100}=0.10\]
Щоб перетворити десяткове число в відсоток, запишіть десяткове число у вигляді дробу. Якщо знаменник дробу не 100, переведіть його в дріб зі знаменником 100, а потім запишіть дріб у відсотках.
\[0.833=\dfrac{833}{1000}=\dfrac{83.3}{100}=83.3\%\]
Щоб перетворити дріб у відсоток, спочатку перетворіть дріб у десятковий, а потім перетворіть десятковий у відсоток.
\[\dfrac{3}{4}=0.75=\dfrac{75}{100}=75\%\]
Припустимо, дослідник виявляє, що 15 з 23 учнів у класі є носіями менінгітидів Neisseria. Який відсоток студентів є носіями? Щоб знайти це значення, спочатку висловіть числа у вигляді дробу.
\[\mathrm{\dfrac{carriers}{total\: students}}=\dfrac{15}{23}\]
Потім розділіть чисельник на знаменник.
\[\dfrac{15}{23}=15\div 23 \approx 0.65\]
Нарешті, щоб перетворити десяткове число в відсоток, помножте на 100.
\[0.65 \times 100=65\%\]
Відсоток студентів, які є носіями, становить 65%.
Ви також можете отримати дані про виникнення та невиникнення; наприклад, у вибірці студентів 9 позитивних тестів на антитіла до токсоплазми, тоді як 28 тестували негативними. Який відсоток серопозитивних студентів? Насамперед необхідно визначити «ціле», частиною якого є позитивні учні. Для цього підсумуйте позитивні і негативні тести.
\[\mathrm{positive+negative=9+28=37}\]
Вся вибірка складалася з 37 студентів. Частка позитивів становить:
\[\mathrm{\dfrac{positive}{total\: students}=\dfrac{9}{37}}\]
Щоб знайти відсоток учнів, які є носіями, розділіть чисельник на знаменник і помножте на 100.
\ [\ dfrac {9} {37} =9\ div 37\ приблизно 0,24\\
0,24\ раз 100 = 24\%\]
Відсоток позитивних студентів становить близько 24%.
Ще один спосіб подумати про обчислення відсотка - встановити еквівалентні дроби, одна з яких - дріб з 100 як знаменник, і перехресне множення. Попередній приклад буде виражений у вигляді:
\[\dfrac{9}{37}=\dfrac{x}{100}\]
Тепер перехрестимо множимо і вирішуємо для невідомого:
\ [\ begin {вирівнювання}
9\ раз 100 &= 37 x &\ nonumber\\ [5pt]
\ frac {9\ раз 100} {37} &= x & &\ text {Розділити обидві сторони на 37}\ nonumber\\ [5pt]
\ frac {900} {37} &= x & &\ текст {Множення}\ nonumber\ [5pt]
24 &\ прибл х & &\ text {Розділити}\ nonumber
\ end {вирівняти}\]
Відповідь, округлений, той же.
Множення та ділення на десятки
У багатьох галузях, особливо в науках, прийнято множити десяткові числа на ступені 10. Давайте подивимося, що станеться, коли ми помножимо 1,9436 на деякі сили 10.
\ [\ почати {вирівняти}
1.9436 (10) &=19.436\ nnumber\\
1.9436 (100) &=194.36\ nnumber\\
1.9436 (1000) &=1943.6\ nnumber
\ кінець {вирівняти}\]
Кількість знаків, на які рухається десяткова крапка, збігається з кількістю нулів у степені десяти. Таблиця\(\PageIndex{1}\) підводить підсумки.
| Помножити на | Нулі | Десяткова крапка рухається. |
|---|---|---|
| 10 | 1 | 1 місце праворуч |
| 100 | 2 | 2 місця праворуч |
| 1 000 | 3 | 3 місця праворуч |
| 10 000 | 4 | 4 місця праворуч |
Ми можемо використовувати цей шаблон як ярлик для множення на повноваження десять замість множення за допомогою вертикального формату. Ми можемо порахувати нулі в ступені 10, а потім перемістити десяткову крапку, що ж кількість знаків вправо.
Так, наприклад, щоб помножити 45,86 на 100, перемістіть десяткову крапку на 2 розряди вправо.
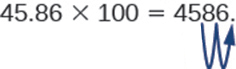
Іноді, коли нам потрібно перемістити десяткову крапку, не вистачає десяткових знаків. У цьому випадку ми використовуємо нулі як заповнювачі. Наприклад, помножимо 2,4 на 100. Нам потрібно перемістити десяткову крапку на 2 розряди вправо. Оскільки праворуч від десяткової крапки є лише одна цифра, ми повинні записати 0 на сотих місцях.
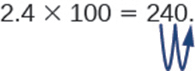
При діленні на ступені 10 просто прийміть протилежний підхід і перемістіть десяткове вліво на число нулів в ступені десяти.
Давайте подивимося, що станеться, коли ми ділимо 1.9436 на деякі повноваження 10.
\ [\ почати {вирівняти}
1.9436\ div 10&=0.19436\ nonumber\\
1.9436\ div 100 & = 0.019436\
nonumber\ nonumber\\ nonumber\ nonumber
{вирівняти}\]
Якщо для переміщення десяткових знаків недостатньо, додайте нулі, щоб створити місця.
Наукові позначення
Наукове позначення використовується для вираження дуже великих і дуже малих чисел у вигляді добутку двох чисел. Перше число виробу, цифрове слово, зазвичай є числом не менше 1 і не більше 10. Друге число добутку, експоненціальний термін, записується як 10 з показником. Деякі приклади наукових позначень наведені в табл\(\PageIndex{2}\).
| Стандартні позначення | Наукові позначення |
|---|---|
| 1000 | 1 × 10 3 |
| 100 | 1 × 10 2 |
| 10 | 1 × 10 1 |
| 1 | 1 × 10 0 |
| 0.1 | 1 × 10 −1 |
| 0,01 | 1 × 10 −2 |
Наукові позначення особливо корисні для дуже великих і дуже малих чисел, таких як 1 230 000 000 = 1,23 × 10 9, і 0.00000000036 = 3,6 × 10 −10.
Висловлення чисел у наукових позначеннях
Перетворення будь-якого числа в наукові позначення є простим. Підрахуйте кількість місць, необхідних для переміщення десяткової коми поруч з крайньою лівою ненульовою цифрою: тобто зробити число між 1 і 10. Потім помножте це число на 10, підняте до кількості знаків, які ви перемістили десяткову. Показник є додатним, якщо ви перемістили десяткову кому вліво і від'ємну, якщо ви перемістили десяткову кому вправо. Так
\[2386=2.386\times1000=2.386\times10^3\]
і
\[0.123=1.23\times0.1=1.23\times10^{-1}\]
Ступінь (показник) 10 дорівнює кількості розрядів, на які зсувається десяткова кома.
логарифми
Загальний логарифм (лог) числа - це ступінь, до якої 10 потрібно підняти, щоб дорівнювати цьому числу. Наприклад, загальний логарифм 100 дорівнює 2, тому що 10 потрібно підняти на другу ступінь, рівну 100. Додаткові приклади наведені в табл\(\PageIndex{3}\).
| Число | Експоненціальна форма | Загальний логарифм |
|---|---|---|
| 1000 | 10 3 | 3 |
| 10 | 10 1 | 1 |
| 1 | 10 0 | 0 |
| 0.1 | 10 −1 | −1 |
| 0,001 | 10 −3 | −3 |
Щоб знайти загальний логарифм більшості чисел, вам потрібно буде скористатися кнопкою LOG на калькуляторі.
Округлення та значущі цифри
При повідомленні числових даних, отриманих за допомогою вимірювань, ми використовуємо лише стільки значущих цифр, скільки гарантує точність вимірювань. Наприклад, припустимо, мікробіолог за допомогою автоматизованого лічильника клітин визначає, що в літровій пробі річкової води налічується 525 341 бактеріальна клітина. Однак вона записує концентрацію як 525 000 клітин на літр і використовує це округлене число для оцінки кількості клітин, які, ймовірно, будуть знайдені в 10 літрах річкової води. У цьому випадку останні три цифри виміряної величини не вважаються значущими. Вони округлені для обліку змін у кількості клітин, які, ймовірно, відбуватимуться, якби було виміряно більше зразків.
Важливість значущих цифр полягає в їх застосуванні до фундаментальних обчислень. Крім того, сума або віднімання, сума або різниця повинні містити стільки цифр праворуч від десяткового числа, скільки в найменш певних (позначено підкресленням у наступному прикладі) чисел, використовуваних при обчисленні.
Припустимо, мікробіолог бажає розрахувати загальну масу двох зразків агару.
\ [\ begin {масив} {l}
4.38\ підкреслення {3}\ текст {g}
\\ підкреслення {3.002\ підкреслення {1}}\ текст {g}\
7.38\ підкреслення {5}\ текст {g}
\ кінець {масив}\]
Найменш певна з двох мас має три знака після коми, тому сума повинна мати три знака після коми.
При множенні і діленні добуток або частка повинні містити не більше цифр, ніж в коефіцієнті, що містить найменшу кількість значущих цифр. Припустимо, мікробіолог хотів би підрахувати, скільки реагенту буде присутній в 6,6 мл, якщо концентрація становить 0,638 г/мл.
\[\mathrm{0.63\underline{8}\:\dfrac{g}{mL}\times6.\underline{6}\:mL=4.1\:g}\]
Знову ж таки, відповідь має лише один десятковий знак, оскільки це точність найменш точного числа при обчисленні.
При округленні чисел збільште збережену цифру на 1, якщо за нею слідує число більше 5 («округлити вгору»). Не змінюйте збережену цифру, якщо наступні цифри менше 5 («округлити вниз»). Якщо за збереженою цифрою слідує 5, округляйте вгору, якщо збережена цифра непарна, або округляйте вниз, якщо вона парна (після округлення збережена цифра, таким чином, завжди буде парною).
Час генерації
Можна написати рівняння для обчислення чисел клітин в будь-який час, якщо відомо кількість початкових комірок і час подвоєння, якщо клітини діляться з постійною швидкістю. Визначимо N 0 як стартове число бактерій, число на час t = 0. N i - кількість бактерій в момент t = i, довільний час в майбутньому. Нарешті, ми встановимо j рівне кількості поколінь, або кількість разів, коли популяція клітин подвоюється протягом часового інтервалу. Тоді ми маємо,
\[N_i=N_0\times2^j\]
Це рівняння є виразом зростання шляхом двійкового ділення.
У нашому прикладі N 0 = 4 кількість поколінь, j, дорівнює 3 через 90 хвилин, оскільки час генерації становить 30 хвилин. Кількість осередків можна оцінити за наступним рівнянням:
\ [\ begin {вирівнювання}
n_i&=n_0\ times2^j\ nnumber\\
N_ {90} &= 4\ times2^3\ nnumber\\
n_ {90} &= 4\ times8=32\ nonumber
\ end {вирівнювання}\]
Кількість клітин через 90 хвилин - 32.
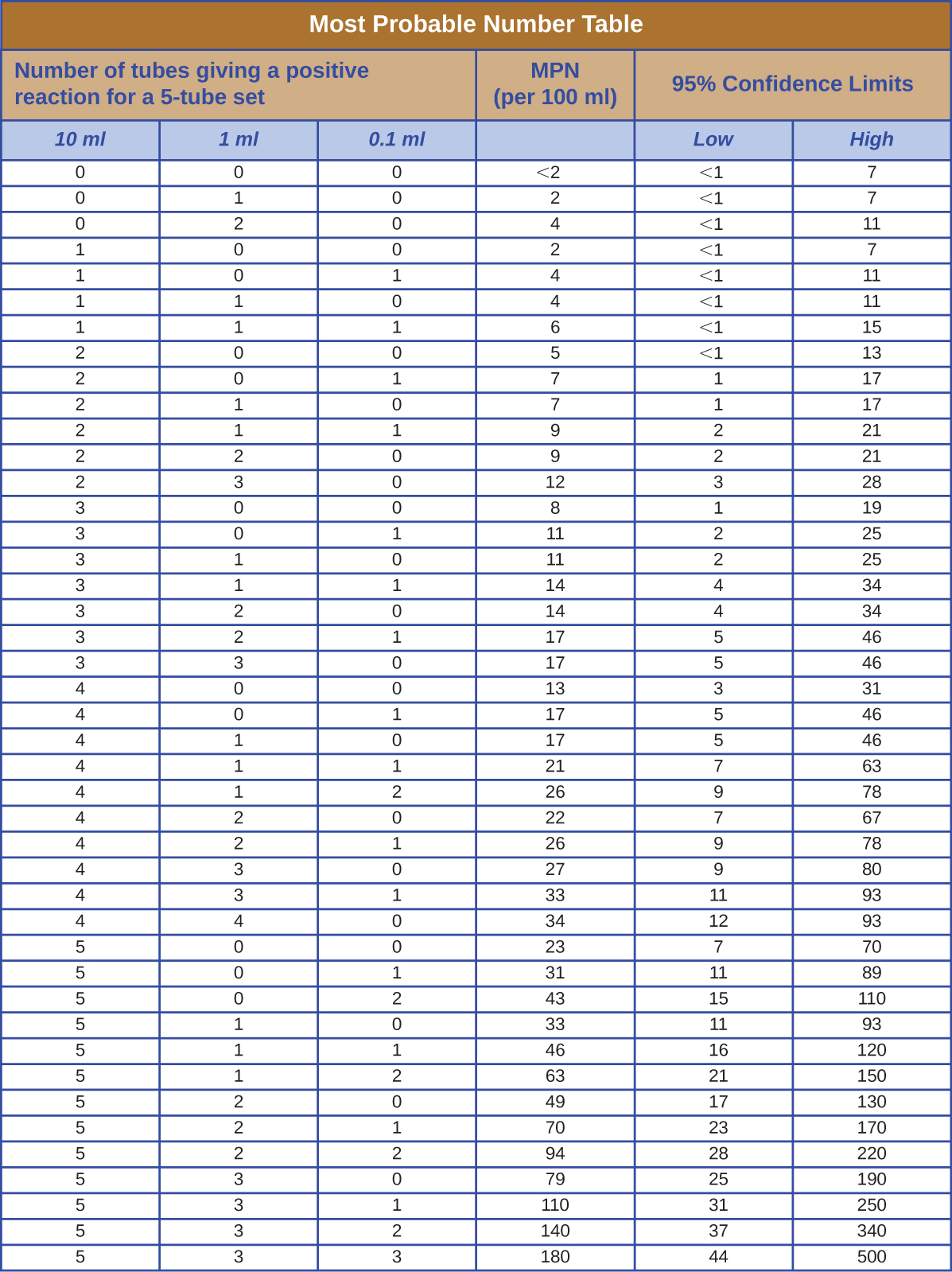
Найбільш ймовірне число
Таблиця на малюнку\(\PageIndex{1}\) містить значення, що використовуються для обчислення найбільш ймовірного прикладу числа, наведеного в розділі Як ростуть мікроби.