9: Відповідь декількох рис на вибір
- Page ID
- 7871
Фітнес організму залежить від результату багатьох різних організмних процесів і фенотипів. Таким чином, природний відбір часто діє на багато фенотипів узгоджено. У деяких випадках різні напрямки, які селекція намагається витягнути фенотипи популяції, можуть бути не всі можливі, щоб задовольнити всіх відразу. Такі компроміси фітнесу виникають, коли селекція суперечливо діє на генетичні корельовані фенотипи.
Щоб зрозуміти короткостроковий наслідок відбору на кілька фенотипів, ми можемо узагальнити рівняння селекціонера до декількох ознак. Враховуючи дві риси, ми можемо написати наші відповіді в обох рисах як
\[\begin{aligned} R_1 & = V_{A,1} \beta_1 + V_{A,1,2} \beta_2 \nonumber \\[4pt] R_2 & = V_{A,2} \beta_2 + V_{A,1,2} \beta_1 \label{eqn:2D_breeders_eqn} \end{aligned}\]
де\(1\) і\(2\) індексувати наші дві різні риси. \(V_{A,2}\)Ось\(V_{A,1}\) і адитивна генетична дисперсія для ознак\(1\) і\(2\) відповідно, в той час як\(V_{A,1,2}\) наша адитивна коваріація між нашими ознаками. Наш градієнт вибору для ознаки 1\(\beta_1\), являє собою зміну придатності, коли ви змінюєте рису 1 поодинці, тримаючи інші риси постійної постійної. Їх\(\beta\) можна оцінити за допомогою багатоваріантної регресії, див. Нижче. Багатоваріантне рівняння селекціонерів - це твердження про те, що наша реакція на будь-який один фенотип модифікується відбором на інші ознаки, які генетично коваріюються з цією ознакою.
Ми також можемо записати це еквівалентно в матричній формі, для довільної кількості ознак. Написання нашої зміни в середньому наших декількох фенотипів у поколінні як вектор\(\bf{S}\) і наша відповідь на кілька поколінь як вектор\(\bf{R}\). Ці дві величини пов'язані
\[\bf{R} = \bf{G} \bf{V_P}^{-1} \bf{S} = \bf{G} \boldsymbol{ \beta} \label{eqn:MV_breeders_eqn}\]
де\(\bf{V_P}\) і\(\bf{G}\) є нашими матрицями дисперсії-коваріації фенотипів і адитивних генетичних значень (Equation\ ref {G_matrix] [P_matrix]}) і\(\boldsymbol{\beta}\) є вектором градієнтів відбору (тобто зміна всередині покоління як частка від загального фенотипічна дисперсія). Зауважте\(\boldsymbol{\beta} = \bf{V_P}^{-1} \bf{S}\), що такий, що кожен\(\beta\) представляє градієнт виділення на ознаці, що враховує його фенотипові коваріації з іншими ознаками.

Прикладом результату селекції на множинні фенотипи розглядають сутички селекції, виміряні в середньому грунті Дарвіновим в'юрком (Geospiza fortis). У 76 році вони вимірювали 634 птахів, з яких\(15\%\) збереглися лише до 1977 року. Птахи, які вижили, були важчими і мали довші, глибші купюри, ніж середні.
| риса | Середнє значення перед відбором (1976) | S | \(\beta\) | Середнє наступне покоління (1978) |
|---|---|---|---|---|
| Вага | 16.06 | 0,74 | \ (\ бета\) ">0.477 | 17.13 |
| Довжина купюри | 10.63 | 0,54 | \ (\ бета\) ">-0.144 | 10,95 |
| Білл Глибина | 9.21 | 0,36 | \ (\ бета\) ">0.528 | 9.70 |
Враховуючи фенотипові коваріації серед ознак (\(\bf{V_P}^{-1}\)), вони виявили, що як вага, так і глибина купюри показали прямий спрямований відбір до більших значень (позитивних\(\beta\) s). Однак довжина купюри показала слабкий вибір до коротших дзьобів (негативних\(\beta\)), що відображає той факт, що довжина купюри показує позитивну фенотипічну кореляцію з глибиною та вагою купюри, і більша частина прямого відбору була на вагу та глибину купюри, перетягуючи довжину купюри вздовж. Дивлячись на наступне покоління, всі три ознаки значно збільшилися завдяки сильним позитивним генетичним кореляціям між ознаками (Таблиця\ ref {table:Geospiza_fortis_VG}). Таким чином, незважаючи на вибір, можливо, сприяє меншій довжині рахунків і, звичайно, не сприяє довгим купюрам, довжина купюри збільшилася в наступному поколінні завдяки позитивній генетичній коваріації з двома ознаками, які вибір діяв для збільшення.
| Wt | БЛ | БД | |
|---|---|---|---|
| Wt | 0,85 | ||
| БЛ | +0.95 | 0,67 | |
| БД | +0.87 | +0.9 | 0,81 |
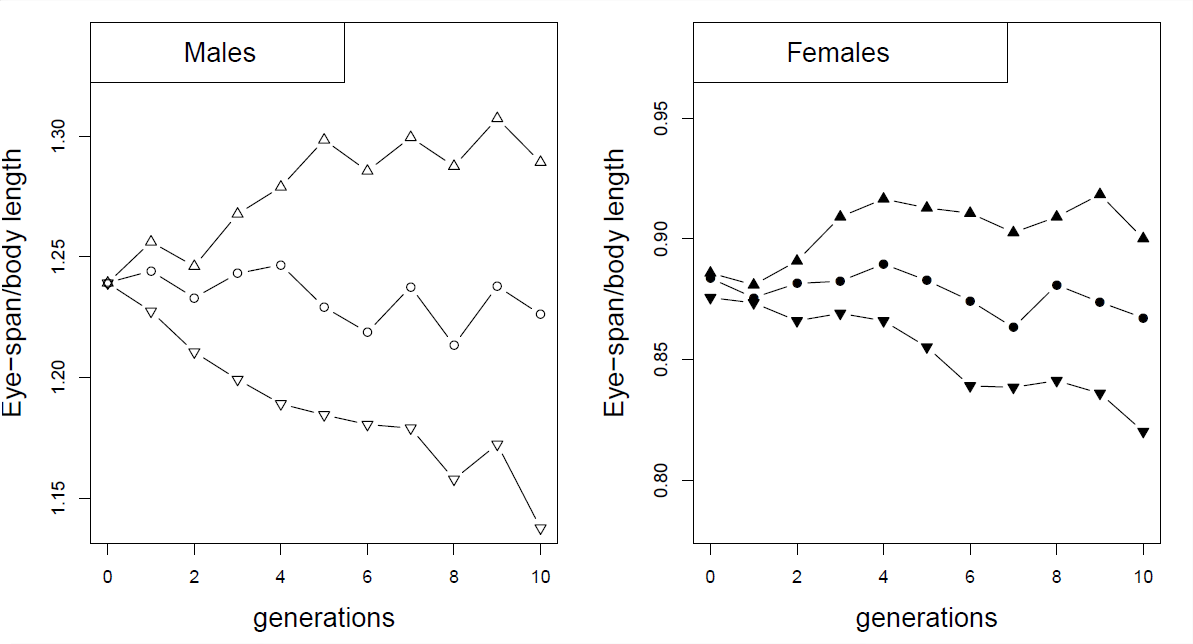
Як приклад корельованих відповідей на селекцію розглянемо селекційний експеримент на стеблооких мухах (Cyrtodiopsis dalmanni). Стеблоокі мухи еволюціонували дивно довгі очні стебла. У лабораторії встановлено шість популяцій диких спійманих мух і відібрано вгору і вниз на чоловічому стеблі та співвідношенні розмірів тіла протягом 10 поколінь (зліва ділянка на малюнку\(\PageIndex{2}\)). Незважаючи на те, що він не вибирав на самок, він бачив корельовану відповідь у самок з кожної з ліній (правий сюжет), через генетичну кореляцію пропорцій чоловічого і жіночого тіла.
_(4561140578).jpg)
Наприкінці десяти поколінь i n 's e experiment (Рисунок\(\PageIndex{3}\)), самці від вгору- і вниз вибраних ліній мали середнє співвідношення очей до тіла\(1.29\) і\(1.14\) відповідно, тоді як самки від вгору- і вниз вибраних ліній мали засоби \(0.9\)і\(0.82\).
- підрахував, що при виборі верхнього/нижнього 10 самців він змістив середнє співвідношення тіла на 0,024 в середньому в межах кожного покоління (це різниця між середнім показником популяції і середнім показником батьків в наступному поколінні). Що таке чоловіча спадковість співвідношення очного стебла до довжини тіла?
- Припустимо, що адитивна генетична дисперсія чоловічого та жіночого фенотипів є рівними і що в цьому експерименті немає прямого відбору пропорції жіночого тіла, тобто що вся реакція у жінок обумовлена корельованим відбором. Чи можете ви оцінити генетичну кореляцію співвідношення очних стебел між чоловіками та жінками?
Фенотипи вцілілих змій. Зверніть увагу, як змії у верхньому лівому та нижньому правому куті представлені в тих, хто вижив. Дані з\ citet {brodie1992 кореляційний}\ gitcode {https://github.com/cooplab/popgen-no...akes_Brodie.R}.
Оцінка багатоваріантних градієнтів вибору
Ми можемо оцінити багатовимірні спрямовані (\(\beta\)) та квадратичні градієнти виділення (\(\gamma\)) так само, як ми робили для окремих рис (\(x_1\)і\(x_2\)), використовуючи лінійні та квадратичні моделі (в eqn\ ref {fitness_regression_} та\ ref {fitness_regression_ колоти}). Наприклад, для двох рис ми можемо написати
\[w_i \sim \beta_1 x_{1,i} + \frac{1}{2} \gamma_1 x_{1,i}^2 + \beta_2 x_{2,i} + \frac{1}{2} \gamma_2 x_{2,i}^2 + \gamma_{1,2} x_{1,i} x_{2,i} + \bar{w} \label{fitness_regression_MV}\]
де\(\beta_1\) і\(\gamma_1\) є спрямованими та квадратичними градієнтами виділення для першої ознаки та аналогічно для черги два. Градієнт вибору коваріації між ознаками задається за допомогою\(\gamma_{1,2}\). Цю методику вимірювання багатовимірного вибору іноді називають «регресією Ланда-Арнольда».
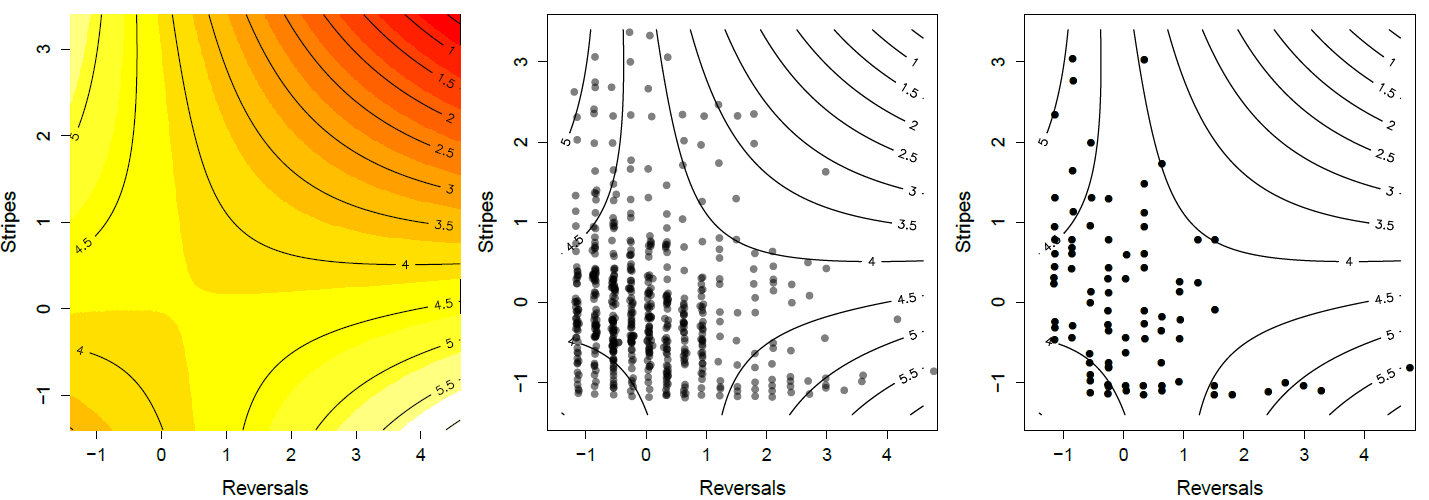
робота забезпечує приємний приклад відбору на множинних рисах уникнення хижаків у північно-західних зміях підв'язки (Thamnophis ordinoides). випустили сотні змій, народжених в лабораторії, в дику природу, а потім виконали спостереження за відстеженням своєї долі. Перш ніж випустити їх, він виміряв, наскільки вони смугасті, і їх поведінкову схильність до розворотів напрямку під час імітації польоту від хижака. Його квадратична поверхня придатності показана на малюнку\ ref {fig:garter_snakes_brodie}, заснованому на підгонці регресії, заданої Equation\ ref {Fitness_regression_mv}, до виживання неповнолітніх. Він виявив, що ні одна ознака спрямованих, ні квадратичних градієнтів не були значними, тобто не було явного виділення на одній рисі, ігноруючи іншу. Однак спостерігався значний негативний вибір коваріації (\(\gamma_{1,2}<0\)). Особи з найвищим шансом на виживання або сильно смугасті і виконують кілька розворотів (верхній лівий кут), або мають невеликий смугастий, але зворотний курс часто (нижній правий кут).

Багатоваріантні фітнес-пейзажі
В останньому розділі ми побачили, що ми часто можемо думати про наше населення, що рухається через середній фітнес-ландшафт. Вибір за єдиною ознакою, що відповідає нашому населенню, роблячи кроки, які піднімаються на найближчий пік фітнесу. Аналогічно наша багатофункціональна реакція на вибір (часто) може розглядатися як наше населення, що піднімається на середній фітнес-ландшафт (див. Рисунок\(\PageIndex{6}\)). Однак шлях нашого населення зараз залежить від генетичних кореляцій.
Раніше ми бачили, що наш єдиний градієнт вибору ознак може бути записаний як\(\beta= \frac{1}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x}}\) (якщо фітнес незалежний від частоти,\ ref {eqn:proof_landscape}). Це стосується кожної нашої риси, тому ми можемо переписати рівняння селекціонерів з двома ознаками (Equation\ ref {EQN:2D_breeders_EQN}) як
\[\begin{aligned} R_1 & = \frac{V_{A,1}}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x_1}} + \frac{ V_{A,1,2}}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x_2}} \nonumber \\[4pt] R_2 & = \frac{V_{A,2}}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x_2}} + \frac{ V_{A,1,2}}{\bar{w}} \frac{\partial \bar{w}}{\partial \bar{x_1}}\label{eqn:2D_fitness_breeders_eqn}\end{aligned}\]
Якщо немає адитивної генетичної кореляції між ознаками (\(V_{A,1,2}=0\), ліва панель малюнка\(\PageIndex{6}\)), то наша популяція просто розвивається до свого місцевого піку фітнесу. Це робить так, як надмірно захоплений альпініст, що йде вгору по найближчому пагорбу, який він знаходить, ледь рухаючись на всіх плоских частинами, але спринт швидко вгору крутіші частини, поки справа доходить до зупинки на вершині пагорба. Якщо нашому населенню не пощастило опинитися на схилах пагорба, який не є найвищим піком, наше населення адаптується і підніметься на цей пагорб, але воно не досягне глобального оптимуму (наприклад, шлях А). Завдяки\(V_{A,1,2}=0\) нашому кожному поколінню розмір кроку для кожної риси незалежний один від одного.
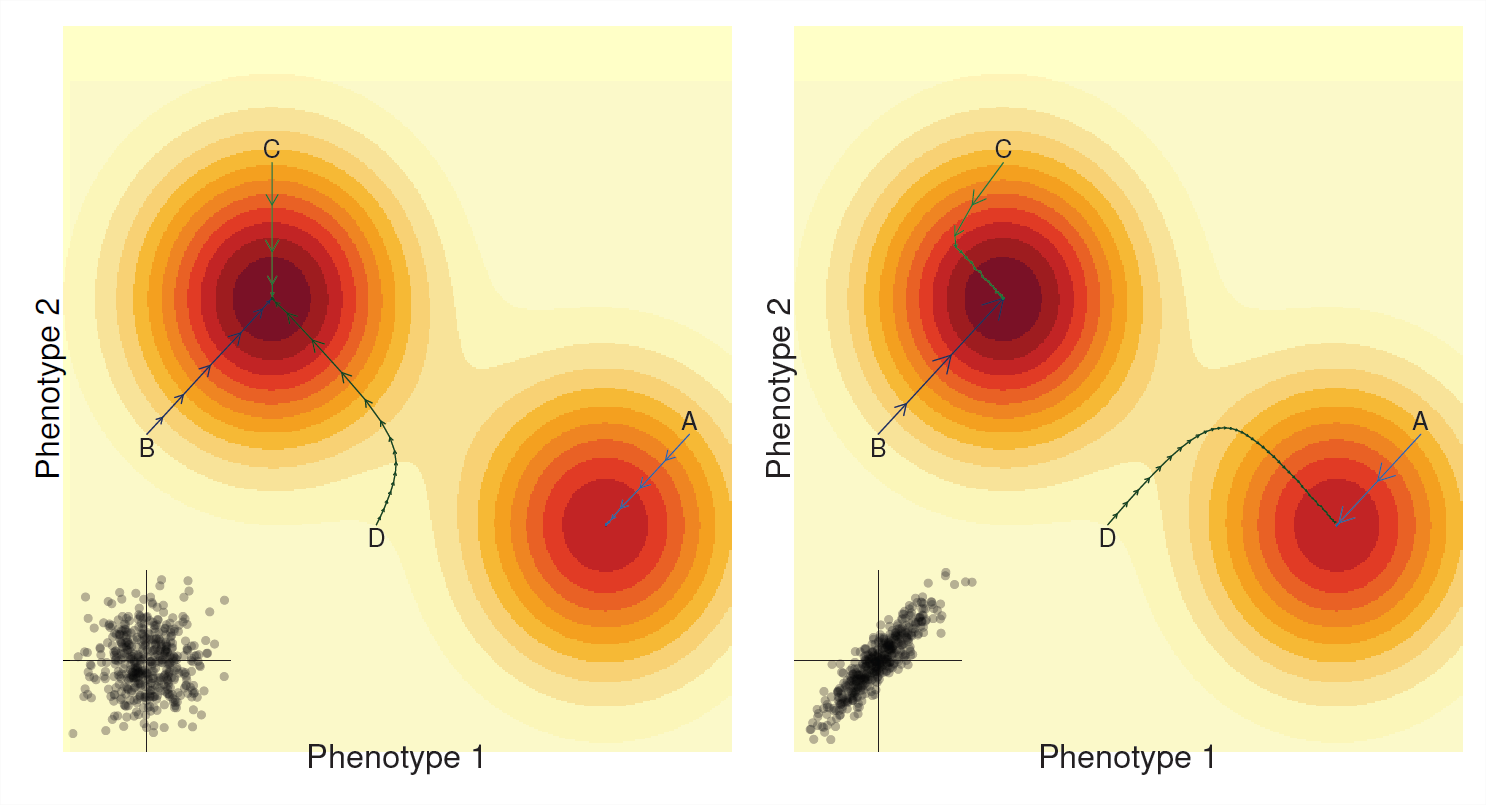
Історія може бути зовсім іншою, якщо між двома фенотипами існує сильна генетична кореляція (правий бік малюнка\(\PageIndex{6}\)), тепер шлях нашого населення упереджений до того, щоб бути сильним вздовж осей генетичної кореляції. Іноді генетична кореляція може допомогти прогресуванню вгору по пагорбу, коли генетична кореляція вирівнюється з нахилом (наприклад, шляхи A і B), оскільки виділення на одному фенотипі підвищує відбір на інший фенотип. Однак генетичні кореляції можуть змусити населення йти дивними шляхами до піків фітнесу, і рух може бути повільним, коли шлях до піку лежить уздовж осі, перпендикулярної коваріації в наших рисах (останні частини шляху C & D) У деяких випадках населення може навіть еволюціонувати до повністю різний пік через генетичних кореляцій (порівняйте шлях D в лівій і правій панелям).
Більш загально, ми можемо розширити це до довільного числа фенотипу, написаного у рівнянні фітнес-ландшафту селекціонера, у матричних позначеннях, як
\[{\bf R} = \frac{1}{\bar{w}} {\bf G} \nabla \bar{w} ({\bar{x}})\]
де\(\nabla\) - оператор векторного градієнта, що приймає похідну за вектором середніх фенотипів, таких що\(\nabla \bar{w} = \left( \frac{\partial \bar{w}}{\partial \bar{x}_1},~ \frac{\partial \bar{w}}{\partial \bar{x}_2},~\cdots \right)\). Таким чином, короткострокова еволюційна реакція населення на відбір полягає у зміщенні його середніх фенотипів (\(R\)) в пряму, що локально збільшує середню придатність населення (\(\nabla_{\bar{x}} \bar{w}\)), але це фітнес-сходження на пагорб нашого населення модерується генетичними коваріаціями. серед наших рис (\({\bf G}\)).
Ідеї про адаптивні фітнес-ландшафти є ключовими для розуміння ролі екології в видобутку. Види можуть зберігатися виразними в умовах схрещування, якщо гібриди між видами погано пристосовані до будь-якої ніші батьківського виду (так званий зовнішній постзиготичний бар'єр для успішної гібридизації). З точки зору фітнес-ландшафту це відповідає видам, що займають різні піки фітнесу, таким чином, що гібриди між двома популяціями, які будуть проміжними за фенотипом, тому потрапляють у долину між вершинами, тобто мають низьку придатність.
Деякі застосування рівняння селекціонера багатовимірного ознак
Багатоваріантне рівняння селекціонерів має багато різних застосувань у розумінні реакції декількох ознак на вибір. Він також пропонує сильне розуміння механістичних основ селекції родичів та статевого відбору. Ми обговоримо їх далі.
Статевий відбір та еволюція переваг матів за допомогою непрямих переваг.
Організми часто докладають величезних зусиль для пошуку та залучення товаришів, іноді за значну вартість своїх шансів на виживання. Чому люди настільки вибагливі щодо того, з ким вони спаровуються, особливо коли їх вибір, здається, базується на складних персонажах та довільних проявах, які, безумовно, знижують життєздатність своїх товаришів?

Однією з основних причин, чому люди розвиваються, щоб бути вибагливими щодо того, з ким вони спаровуються, є те, що це може безпосередньо вплинути на їх фітнес. Вибираючи партнера з певними характеристиками, особини можуть отримати більше батьківської турботи про своє потомство, уникати паразитів або вибирати партнера з більш високою родючістю. Наприклад, самки світлячків спалахують вночі, щоб залучити самців, що пролітають повз. Самки з більшими, більш яскравими ліхтариками мають більш високу плодючість, тому самці з перевагою більш яскравих спалахів отримають пряму користь для власної фітнесу. (Зверніть увагу, що самці отримають користь, навіть якщо ці відмінності в плодючості жінок повністю обумовлені відмінностями в навколишньому середовищі, і, отже, не є спадковими.) Дійсно чоловічі світіння черв'яків еволюціонували, щоб їх приваблювали більш яскраві блимають приманки.

Однак навіть за відсутності прямих переваг вибору вибір все одно може побічно сприяти еволюції вибагливості. Ці непрямі переваги виникають тому, що люди можуть мати більш високу придатність потомства, вибираючи партнера, фенотип якого вказує на високу життєздатність (так звана гіпотеза «хороших генів»), або вибираючи партнера, фенотип якого просто привабливий і, ймовірно, дасть подібне привабливе потомство («втеча» або гіпотеза «сексуальних синів»).

Ми позначимо рису відображення, наприклад, довжину хвоста, у самців\(\mars\) і ознаку переваги у самок по\(\venus\). Наша риса відображення знаходиться під прямим відбором у чоловіків, так що його реакція на вибір може бути записана як
\[R_{\mars} = \beta_{\mars} V_{A, \mars}\]
Припустимо, що жіноча ознака переваги, ступінь, до якої самок приваблюють довгі хвости, не знаходиться під прямим відбором\(\beta_{\venus}=0\). Тоді відповідь на вибір ознаки переваги можна записати як
\[\begin{aligned} R_{\venus} &=\beta_{\venus}V_{A,\venus} + \beta_{\mars} V_{A, \venus \mars} & = \beta_{\mars} V_{A, \venus \mars}\end{aligned}\]
Так що жіноче перевагу буде відповідати відбору, якщо воно генетично співвідноситься з чоловічою ознакою, тобто якщо не\(V_{A, \venus \mars}\) дорівнює нулю. Існує ряд різних способів виникнення цієї генетичної кореляції; найпростішим є те, що локуси, що лежать в основі чоловічої риси, можуть мати плейотропний вплив на переваги жінок. Однак уподобання жінок часто можуть мати досить виразну генетичну основу від чоловічих ознак прояву.
Більш загальний спосіб, при якому можуть виникнути генетичні кореляції ознаки-переваги, - це асортативне спарювання. Оскільки самки змінюються у своїх перевагах довжини хвоста, ті, хто віддає перевагу довшим хвостикам, будуть спаровуватися з довгохвостими самцями, а навпаки - для самок з перевагою коротших хвостів. Таким чином, генетична кореляція між ознаками відображення і переваги буде встановлена (див. Рис.\ ref {fig:assort_mating_2_trait}).
Самці з довшими хвостами також несуть алелі, пов'язані з перевагою довших хвостів, оскільки їхні довгохвості тато, як правило, спаровуються з самками з генетичною перевагою довгих хвостів. Аналогічно самці з більш короткими хвостами будуть носити алелі, пов'язані з перевагою коротших хвостів. Таким чином, якщо є прямий відбір для самців з більш довгими хвостами, то перевага самки більш довгих хвостів теж збільшиться, оскільки це генетично корелює за допомогою асортативного спарювання.

Як приклад того, як прямий відбір ознак відображення може стимулювати еволюцію ознак переваги, розглянемо деякі дані з гуппі. Гуппі (Poecilia reticulata) - класична система вивчення взаємодії природного і статевого відбору. У деяких популяціях гуппі самки віддають перевагу самцям з більш помаранчевим забарвленням.

встановили чотири репліковані популяції пар гуппі і вибрали по одній з кожної пари для збільшення або зменшення помаранчевого забарвлення у самців, вибираючи верхній/нижній\(20\) з\(50\) самців. Вона випадковим чином вибирала самок з кожної популяції, щоб сформувати наступне покоління, і тому не робила прямого відбору на самок. Вона виміряла реакцію на виділення на чоловічому забарвленні та на жіночу перевагу для оранжевого (ліва та права панелі Figure\ ref {fig:assort_mating_guppies} відповідно). У лініях, які підбиралися для більш помаранчевих самців, самки демонстрували підвищену перевагу помаранчевому. Хоча в тих лініях, вибраних для менш помаранчевих у чоловічих дисплеях, жінки показали зниження переваги помаранчевого. Це узгоджується з непрямим відбором на переваги жіночого помаранчевого кольору як відповідь на виділення на чоловіче забарвлення, через генетичну кореляцію між жіночими уподобаннями та чоловічими ознаками. Апріорі малоймовірно, що плейотропія є джерелом генетичної кореляції між цими ознаками, швидше за все, це спричинено самоками, асортно спаровуючись з самцями, які відповідають їх колірним уподобанням.
Повертаючись до нашого прикладу пташиного хвоста, що може призвести до прямого відбору довжини хвоста самця? Вибір довших хвостів у самців може відбутися тому, що довші хвости генетично корелюють з вищою життєздатністю чоловіків, наприклад, можливо, лише самці, які збирають надлишок їжі, мають ресурси для інвестування у вирощування довгого хвоста, тобто довгий хвіст є чесним сигналом придатності. Це відповідало б поясненню «хороших генів» еволюції вибору жіночої статі.
Існує ще один тонкий спосіб, який вибір може сприяти нашій чоловічій рисі. Уявіть, що варіація жіночої ознаки переваги полягає в тому, що деякі самки не мають сильної переваги довжині чоловічого хвоста, але деякі самки мають сильну перевагу самцям з довшими хвостами.

Самці з довшими хвостами мали б вищу плодючість, ніж самці з коротким хвостом, оскільки є підмножина самок, яких сильно приваблюють довгі хвости, і ці самці також можуть спаровуватися з іншими самками. Таким чином, відбір сприяє довгохвостим самцям, і тому опосередковано віддає перевагу жінкам довшим хвостикам; самки, які віддають перевагу довшим хвостикам, мають синів, які, в свою чергу, більш привабливі. Цю модель іноді називають моделлю sexy-son. Його також називають моделлю Fisherian втікача, оскільки жіночі переваги та чоловіча риса можуть співрозвиватися в ескалації моди, що рухає все більш екстремальними уподобаннями для довільних рис. Таким чином, багато екстравагантних рис відображення у чоловіків і жінок можуть існувати чисто тому, що люди вважають їх красивими і приваблюють їх.
Правило Гамільтона та еволюція альтруїстичної та егоїстичної поведінки
«Єдина причина для того, щоб зробити шум, про який я знаю, - це те, що ти бджола». Тоді [Пух] подумав ще довгий час і сказав: «Єдина причина того, щоб бути бджолою, про яку я знаю, - це робити мед... І єдина причина виготовлення меду - це те, що я можу його їсти». —Вінні-Пух,.
Одним із сейсмічних зрушень, викликаних роботою Дарвіна, було усвідомлення того, що організми не існують на користь інших особин чи інших видів. Бджоли не еволюціонували, щоб запилювати квіти, більше, ніж вони еволюціонували, щоб зробити мед для ведмедів. Якщо ми можемо сказати, що існує «причина», чому організм існує, це лише залишити потомство наступному поколінню. Пуха можна пробачити за те, що він відхилявся від дарвінівської думки, оскільки він існує на користь Крістофера Робіна та інших дитячих історій на ніч.
Однак у цьому дарвінівському погляді є зморшка. Робочі бджоли не роблять мед, щоб принести користь своєму потомству, вони стерильні і працюють на благо бджолиної королеви та її потомства. Люди часто поводяться таким чином, що жертвують власною придатністю на благо інших. Те, що відбір сприяє таким очевидним актам альтруїзму, на перший погляд. постачається перше загальне еволюційне пояснення такого альтруїзму. Його інтуїція полягала в тому, що хоча індивід втрачає деякий репродуктивний вихід, алелі, що лежать в основі альтруїстичної поведінки, все ще можуть поширюватися в популяції, якщо ця вартість переважується вигодами, отриманими через передачу цих алелів через пов'язану людину. Зверніть увагу, що це означає, що алель не діє самопожертвуючи чином, навіть якщо люди можуть в результаті.
Альтруїзм відображає соціальні взаємодії. Отже, як проста модель, давайте уявимо, що люди взаємодіють парами, а наш фокусний\(i\) індивід поєднується з індивідом\(j\). Уявіть, що у людей є два можливі фенотипи\(X=1\) або\(0\), що відповідає наданню або утриманню якогось невеликого акту «альтруїзму» (ми могли б так само легко перевернути ці мітки і назвати їх безкорисливим вчинком і егоїстичним вчинком відповідно). Наші пари особин, які взаємодіють, можуть, наприклад, бути братами та сестрами, що розділяють гніздо. Альтруїстична риса може бути такою ж простою, як зростання дещо повільнішими темпами, щоб зменшити конкуренцію братів і сестер за їжу від батьків, або більш складні акти альтруїзму, такі як діти, які попереджають власне відтворення, щоб допомогти батькам виховувати своїх братів і сестер.
Забезпечення альтруїстичного акту має витрати\(C\) на придатність нашої особистості, і ненадання цього акту не має жодних витрат. Отримання цього альтруїстичного акту надає користь\(B\) фітнесу особам, які не отримали цього акту. Правило стверджує, що така риса буде поширюватися по населенню, якщо
\[2F B > C\]
де\(F\) - середній коефіцієнт спорідненості між взаємодіючими особинами (\(i\)і\(j\)). У звичайному формулюванні Правило Гамільтона наш\(2F\) замінений на «Коефіцієнт відносин», який є часткою алелів, поділених між особами. Тут ми використовуємо дворазовий коефіцієнт спорідненості, щоб тримати речі відповідно до наших позначень для цих глав. Зверніть увагу, що якщо наші особини самі інбредні, нам потрібно зробити трохи обережніше, щоб узгодити ці дві заходи. Таким чином, альтруїстична поведінка буде поширюватися, навіть якщо це дорого для людини, якщо його вартість окупається вигодою для достатньо пов'язаних осіб.
Як один із прикладів відбору родичів розглянемо роботу з кооперативного залицяння у диких індиків (Meleagris gallopavo). Індики-самці часто формують партнерські відносини з підлеглим чоловіком, допомагаючи домінуючому самцю показуючи самцям та захищаючи самок від інших груп самців.

Ці пари часто є повноправними братами (\(F=0.25\)), при цьому підлеглий чоловік часто є молодшим з двох. Підлеглий самець часто втрачає можливості спарювання протягом усього життя, виступаючи як вінгмен для своїх старших братів. підрахував, що домінуючі самці отримали додаткове\(6.1\) потомство, коли вони відображаються з партнером, ніж чоловіки, які відображаються поодинці. Підлеглі самці програють на батьківському\(0.9\) потомстві в порівнянні з одиночними самцями. Таким чином, витрати на допомогу підлеглих чоловіків з лишком компенсуються прибутками їхніх братів (\((2 \times 0.25) \times 6.1 > 0.9\)), і тому еволюція цієї альтруїстичної допомоги у кооперативному залицянні потенційно добре пояснюється відбором родичів.
Як би ця відповідь була змінена, якби чоловічі партнерські стосунки Туреччини були лише\(\frac{1}{2}\) сибами або першими двоюрідними братами?
[Рис: Гамільтон _B_C]
Звідки береться цей результат? Ну, ми можемо використовувати нашу кількісну генетичну структуру, щоб отримати деяку інтуїцію, виводячи просту версію Правила Гамільтона, думаючи про фенотипи родичів людини як генетично корельованих фенотипів. Щоб намалювати доказ цього результату, припустимо, що придатність нашого фокусного\(i\) індивіда може бути записана як
\[W(i,j)= W_0 + W_i +W_j\]
де\(W_i\) внесок придатності індивіда\(i\) завдяки власному фенотипу, і внесок у\(W_j\) придатність нашої\(i\) особистості завдяки поведінці\(j\) взаємодіючої людини (тобто \(j\)фенотип). З вигодою\(B\) і вартістю\(C\) наші\(W(i,j)\) зображені на малюнку\ ref {рис:Hamilton_b_c}.
Дотримуючись нашого багатоваріантного рівняння селекціонера, ми можемо записати очікувану зміну нашого поведінкового фенотипу як
\[R = \beta_i V_A + \beta_j V_{A,i,j},\]
Наш альтруїстичний фенотип зростає в популяції\(R>0\), якщо, тобто якщо
\[\beta_i V_A + \beta_j V_{A,i,j} > 0\]
\(\beta_i\)Нахил регресії поведінкового фенотипу нашого фокусного індивіда на фітнес пропорційний\(-C\). Нахил\(\beta_j\) регресії фенотипу нашого взаємодіючого партнера на придатність нашого фокусного індивіда пропорційний\(B\) (з тією ж константою пропорційності). Тому наш альтруїстичний фенотип збільшується в популяції, якщо
\[\begin{aligned} \beta_i V_A + \beta_j V_{A,i,j} & > 0 \nonumber \\ B \frac{V_{A,i,j}}{V_A} & > C \label{eqn:Covar_Hamilton}\end{aligned}\]
Отже, яка середня генетична коваріація між індивідуальним\(i\) та\(j\) альтруїстичним фенотипом? Це однаковий поведінковий фенотип у обох осіб, тому фенотипи генетично корелюють, якщо наші індивіди пов'язані один з одним. Коваріація одного фенотипу між двома особами справедлива\(2 F_{i,j} V_A\) (див.\ ref {additive_covar_general_rellys}). Отже, наш альтруїстичний фенотип збільшується в популяції, якщо
\[\begin{aligned} B\frac{2 F_{i,j} V_A}{V_A} &> C \nonumber \\ 2 F_{i,j} B & > C \label{eqn:Hamiltons_rule}\end{aligned}\]
З цієї точки зору правило - це просто твердження про те, що альтруїстична поведінка може поширюватися за допомогою відбору родичів, якщо середня вартість індивіда відображення альтруїстичного фенотипу, тобто проведення альтруїстичних алелів, окупається через середню вигоду взаємодії з альтруїстичними родичами (родичами).

Під родиною селекції спорідненість та племінна структура популяцій є ключовим фактором у визначенні еволюції альтруїстичної поведінки. Одним з найбільш вражаючих прикладів еволюції альтруїзму є повторна еволюція еусоціалізму, де стерильні касти еволюціонували, щоб допомогти виховувати своїх братів і сестер, а не власне потомство. Eusociality еволюціонувала щонайменше вісім незалежних разів у перетинчастокрилих (бджіл, ос та мурах). Існує величезна різниця в системах спаровування перетинчастокрилих від високого рівня багаторазового спаровування до монардії. провели порівняльний філогенетичний аналіз системи спарювання у сотень видів перетинчастокрилих. Вони виявили, що кожен з восьми еусоціальних кладів мав монастир, самки, що спаровуються з одним самцем, як родова держава. Таким чином, еусоціальність спочатку розвивалася в популяціях, де спорідненість була максимізована серед братів і сестер.

Інші форми альтруїзму
Кін-селекція може сприяти альтруїзму, оскільки особи, що несуть альтруїстичні алелі, взаємодіють з іншими пов'язаними особами, які, як правило, демонструють альтруїстичні фенотипи і таким чином отримують перевагу. Однак є й інші способи поширення альтруїстичної поведінки, ніж просто через взаємодію з родичами.
Існує властива проблема співпраці між неродичами. Шахраї часто виграють. Щоб побачити скрутне становище співпраці, давайте розглянемо класичну дилему в'язня. Уявіть, що двох злочинців спіймає поліція, недостатньо доказів, щоб отримати їх за основним звинуваченням, але вони будуть засуджені за меншим звинуваченням. Ув'язнені погано знають один одного, вони ніколи раніше не працювали разом. Їм загрожує рік в'язниці кожен за меншим звинуваченням. Поліція пропонує кожному ув'язненому угоду, свідчать проти вашого співвідповідача і ми знімемо всі звинувачення проти вас, ваш співвідповідач отримає три роки. Якщо вони обидва вирішать продати, вони отримають два роки. Найкращий комбінований результат для підсудних - співпрацювати один з одним і мовчати, кожен з них буде служити рік. Однак обвинувачені не можуть порадитися, і кожен не має можливості дізнатися, чи виверещав інший і розганяв його. Раціональний вибір в цьому разовому взаємодії - розпродати свого побратима. Є багато таких ситуацій, коли взаємодія між людьми має найкращий результат, якщо вони працюють разом. Однак, оскільки люди можуть обдурити взаємодію, раціональним результатом може бути не співпраця. Щоб помістити це в еволюційну обстановку, ми могли б уявити, що придатність організмів у популяції залежала від їх стратегій в одноразовій грі з дилемою в'язня, наприклад, випадкове сполучення людей. У таких налаштуваннях людина, що обманює, матиме вищу придатність, ніж альтруїст, і тому населення буде розвиватися до всіх обманів. І все ж співпраця між неродичами розвивалася багато разів.
| Безшумний (співпрацює) | Зізнається (Коди) | |
|---|---|---|
| Безшумний (співпрацює) | 1, 1 | 3, 0 |
| Зізнається (Коди) | 0, 3 | 2, 2 |
Ключовим фактором, що призвело до некооперативної поведінки в дилемі цього ув'язненого, був одноразовий характер взаємодії. Оптимальна стратегія змінюється, коли наші партнери стикаються з цією ситуацією разом кілька разів, наприклад, якщо члени нашої банди регулярно втягуються протягом багатьох років свого життя у злочині. Інтуїтивно, якщо хтось із наших ув'язнених знає, що її член банди не зрадив її в останній раз, то ви можете очікувати, що вона буде більш схильна довіряти їм і не зраджувати їх цього разу. Ця установка називається ітераційною дилемою в'язня, коли наші ув'язнені стикаються з «грою» з витратами та вигодами неодноразово, знаючи, як інший гравець поводився на попередніх раундах гри. у цій ітераційній обстановці можлива проста стратегія «tit-for-tat». Гравці, дотримуючись цієї стратегії, починають гру, співпрацюючи, а потім копіюють стратегію іншого ув'язненого з останнього ходу (якщо інший ув'язнений співпрацював останній раз, коли вони співпрацюють цього разу, і аналогічно для обману). Уявіть собі знову нашу популяцію організмів, які тепер випадково парні, щоб грати в ітераційні ігри для їх фітнесу. Якщо багато людей у популяції грають стратегію «tit-for-tat», обманююча людина в цій популяції має нижчу придатність, ніж людина, що відповідає за тат. Особи, які грають стратегію «tit-for-tat», не співпрацюють з шахраями, і тому платять невеликі відносні витрати за взаємодію з цими особами, але вони отримують переваги співпраці з іншими альтруїстичними особами. Таким чином, «взаємний альтруїзм», коли люди надають дорогу допомогу особам, яких вони очікують, відповість взаємністю в деяку майбутню дату, може розвиватися. Зауважте, що немає нічого справді альтруїстичного щодо взаємного альтруїзму, взаємодіючі люди просто діють, щоб збільшити свою пряму придатність протягом усього життя, і як така взаємодія взаємовигідна. Таким чином, деякі віддають перевагу назві «взаємність», а не «взаємний альтруїзм».
Ми можемо використовувати нашу систему правил Гамільтона, щоб більш детально зрозуміти еволюцію взаємного альтруїзму. Єдині вимоги до правила Гамільтона щодо прогнозування поширення альтруїстичної поведінки полягає в тому, що
\[\begin{aligned} B \frac{Cov(X_i,X_j)}{V_A} & > C \end{aligned}\]
це те саме, що Equation\ ref {EQN:Covar_Hamilton}, де зараз ми виписали\(V_{A,i,j}\) як коваріацію між поведінковим фенотипом нашої фокальної особистості\(i\) та взаємодіючими особами\(j\).

Тому нам потрібен достатньо позитивний рівень коваріації між альтруїстичною поведінкою індивіда\(i\) та поведінкою взаємодіючих людей, щоб переважити витрати, тобто альтруїсти досить часто взаємодіють з альтруїстами, щоб дозволити альтруїстичним особам, які платять витрати в середньому. отримувати фітнес-переваги від інших осіб. За моделями селекції шкіри ця позитивна коваріація походить від позитивної генетичної коваріації, яка взаємодіє з членами сім'ї. Однак ця позитивна коваріація також може виникнути, якщо альтруїсти демонструють контекстно-залежні стратегії, такі як tit-for-tat, де вони лише альтруїстичні щодо людей, які не обманювали їх останнім часом. Зауважте, що ми дійсно розтягуємо наше використання багатовимірного рівняння селекціонера тут, ці коваріації зараз насправді не є генетичними коваріаціями. Ці коваріації не є між рисами одного індивіда або між пов'язаними особами, вони є ознаками коваріацій осіб, які взаємодіють з аналогічними кооперативними особами. Ці взаємодіючі особини тут навіть не повинні бути однаковими видами, оскільки ці моделі можуть бути використані для розуміння еволюції міжвидових мутуалізмів.
Ми знаходимо альтруїзм в деяких, здавалося б, дивних місцях. Кажани-вампіри (Desmodontinae), як випливає з їх назви, харчуються тільки кров'ю інших тварин. Однак кров - це не зовсім суперпродукт, в який Дракула б ви повірили. Кров - це в основному вода. Літаючі неймовірно енергійні, і тому кажанам доводиться споживати половину маси тіла в крові за ніч і швидко помруть, якщо вони пройдуть без їжі. Часто важко знайти достатню кількість крові за ніч, і тому, хто пропускає годування, виживають лише інші кажани, що діляться їжею крові. Кажани вампірів ділять їжу зі своїми родичами, а також з неспорідненими особами. Як передбачав взаємний альтруїзм, вони, як правило, діляться з особами, які раніше ділилися з ними продуктами, таким чином, обмін їжею можна розглядати як адаптивну поведінку.
Природний відбір рідко діє на одну рису ізольовано, скоріше селекція часто діє на багато рис відразу. Таким чином, короткострокова реакція селекції на ознаку також відображає відбір на інші частково генетично корельовані ознаки. Багато еволюційних компромісів, серед різних аспектів фітнесу, можна подумати в цих умовах.
Відповідь між поколіннями декількох ознак на селекцію може бути зрозуміла та передбачена за багатоваріантним (множинним ознаками) рівнянням селекціонера. Відповідь ознаки (\(R_1\)) залежить від адитивної генетичної дисперсії для цієї ознаки та прямого градієнта відбору на ознаці (\(V_{A,1} \beta_1\)), ця пряма відповідь модифікується непрямим відбором на ознаку (и) (\(2\)), що генетично коваріюється ( \(V_{A,12} \beta_2\)).
Ми можемо оцінити лінійні, спрямовані градієнти відбору за багатовимірною лінійною регресією придатності на фенотипах.\(\beta\) Ми можемо включити стабілізуючий, диспрутивний та коваріативний відбір серед ознак, включивши квадратичні терміни для фенотипів у цю регресію.
Ми можемо інтерпретувати багатовимірне рівняння селекціонера з точки зору фітнес-ландшафтного підходу, і побачити, що природний відбір може привести наше населення до місцевих піків середньої придатності. Однак шлях, який він проходить, є упередженим, щоб краще вирівнюватися з генетичними кореляціями між ознаками, що в деяких випадках може уповільнити реакцію нашої популяції на відбір.
Багатоваріантне рівняння селекціонера застосовується в багатьох місцях еволюційної теорії. Наприклад, еволюція непрямого відбору для переваги матів є додатком, оскільки генетична кореляція, встановлена асортативним спаровуванням між ознаками переваги та рисами відображення, є ключовою для розуміння того, чому перевага матів може реагувати на непрямий відбір. Ми також побачили, як можна розробити моделі відбору родичів, щоб зрозуміти альтруїзм та правило Гамільтона, використовуючи багатовимірне рівняння селекціонера, розглядаючи родичів як генетично коваріювану фітнес.
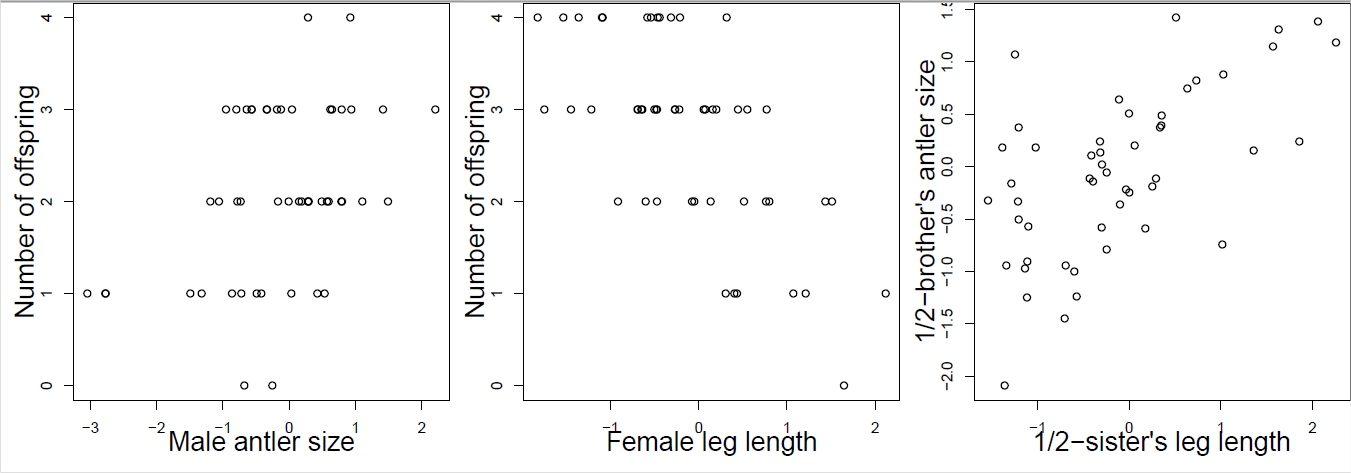
Ви збираєте спостереження благородного оленя протягом покоління, записуючи кількість потомства та фенотипів людини для ряду ознак, які, як відомо, мають адитивні генетичні варіації. Використовуючи свої дані, ви будуєте графіки, показані на малюнку\ ref {fig:red_deer_q} (стандартизація фенотипів). Дайте відповідь на наступні питання, вибравши один із сміливих варіантів. Коротко обґрунтуйте кожну свою відповідь посиланням на рівняння селекціонера та рівняння селекціонера з кількома ознаками.
- Дивлячись лише на фігуру\ ref {Fig:Red_deer_Q} A, в якому напрямку ви очікуєте, що розмір чоловічого рога буде розвиватися? Недостатня інформація, збільшення, зменшення.
- Дивлячись лише на цифри\ ref {Fig:Red_deer_Q} B і C, в якому напрямку ви очікуєте, що розмір чоловічого рога буде розвиватися? Недостатня інформація, збільшення, зменшення.
- Дивлячись на цифри\ ref {Fig:Red_deer_Q} A, B і C, в якому напрямку ви очікуєте, що розмір чоловічого рога буде розвиватися? Недостатня інформація, збільшення, зменшення.