20.5: Статистичні методи

Last updated
Save as PDF

Page ID: 5817

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Що нам говорять дані?

Існує два види числових даних, отриманих біологами:

підрахунок; наприклад, кількість жінок у популяції
вимірювання безперервної змінної, такої як довжина або вага

У першому випадку кожен може домовитися про «істинному» значенні. У другому випадку вимірювані значення завжди відображають діапазон, розмір якого визначається такими факторами, як

точність вимірювального приладу і
індивідуальна мінливість серед вимірюваних об'єктів.

Як обробляються такі дані?

Розрахунок стандартного відхилення

Насамперед необхідно обчислити середнє значення (середнє) для всіх членів множини. Це сума всіх показань, поділена на кількість знятих показань.

Але розглянемо набори даних:

46,42,44,45,43 і 52 80,22,30,36

Обидва дають однакове значення (44), але я впевнений, що ви можете інтуїтивно бачити, що експериментатор мав би набагато більше впевненості в середньому, отриманому з першого набору показань, ніж одне, отримане з другого.

Одним із способів кількісної оцінки розкиду значень у наборі даних є обчислення стандартного відхилення (S) за допомогою рівняння

\[s =\sqrt{ \dfrac{\sum (x-\bar{x})^2}{n-1}}\]

де («x мінус x-bar) ² - квадрат різниці між кожним окремим виміром (x) і середнім («x-bar») вимірювань. Символ сигма позначає суму цих, а n - кількість окремих вимірювань.

Використовуючи перший набір даних, обчислюємо стандартне відхилення 1,6.

альт

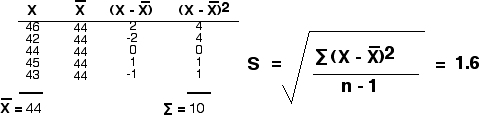
Другий набір даних дає стандартне відхилення 22,9.

альт

(Багато недорогі ручні калькулятори запрограмовані для виконання цієї роботи за вас, коли ви просто вводите значення для X.)

Стандартна похибка середнього

У наших двох наборах з 5 вимірювань обидва набори даних дають середнє значення 44. Але обидві групи дуже маленькі. Наскільки ми можемо бути впевнені, що якщо ми повторюємо вимірювання тисячі разів, обидві групи продовжуватимуть давати середнє значення 44? Щоб оцінити це, обчислимо стандартну похибку середнього значення (S.E.M. або S _x-bar) за допомогою рівняння

\[ S_{\bar{x}} = \dfrac{S}{\sqrt{n}}\]

де S - стандартне відхилення, а n - кількість вимірювань.

У нашому першому наборі даних, S.E.M. 0.7.

\[ S_{\bar{x}} = \dfrac{S}{\sqrt{5}} = \dfrac{1.6}{2.23} = 0.7\]

У другій групі він становить 10,3.

\[ S_{\bar{x}} = \dfrac{S}{\sqrt{5}} = \dfrac{22.9}{2.23} = 10.3\]

95% Ліміти довіри

Виявляється, існує 68% ймовірності того, що «істинне» середнє значення будь-якого вимірюваного ефекту падає між стандартною похибкою +1 і −1 (S.E.M.). Оскільки це не дуже велика ймовірність, більшість працівників вважають за краще розширити діапазон до меж, в яких вони можуть бути на 95% впевнені в тому, що лежить «справжнє» значення. Цей діапазон приблизно від −2 до +2 разів перевищує стандартну похибку.

Так

для нашої першої групи 0,7 х 2 = 1,4
для нашої другої групи 10,3 х 2 = 20,6

Так

якщо наша перша група є репрезентативною для всієї популяції, ми на 95% впевнені, що «справжнє» середнє лежить десь між 42,6 і 45,4 (44 ± 1,4 або 42,6 ≤ 44 ≤ 45,4).
для нашої другої групи ми на 95% впевнені, що «істинне» середнє знаходиться десь між 23,4 і 64,6 (44 ± 20,6 або 23,4 ≤ 44 ≤ 64,6).

Іншим чином, коли середнє значення представлено разом з його 95% межі довіри, працівники кажуть, що є лише 1 з 20 шанс, що «справжнє» середнє значення лежить за межами цих меж.

Поставте ще інший шлях: ймовірність (p) того, що середнє значення лежить за межами цих меж менше 1 з 20 (p = <0,05).

Приклад:

Припустимо, що альт

перший набір даних (» A «) (46,42,44,45,43) являє собою вимірювання п'яти тварин, яким було надано конкретне лікування та
другий набір даних («B») (52,80,22,30,36) вимірювань п'яти інших тварин з різним лікуванням.
Третій набір («С») з п'яти тварин використовувався як контрольний; їм взагалі не давали лікування, а їх вимірювання становили 20,23,24,19,24. Середнє значення контрольної групи - 22, а стандартна похибка - 2,1.

Чи мало лікування А значний ефект? Зробив лікування B?

На графіку показано середнє значення для кожного набору даних (червоні точки). Темні лінії представляють 95% довірчих меж (± 2 стандартні помилки).

Хоча обидва експериментальні засоби (А і В) вдвічі більші за середнє контрольне, лише результати в А є значущими. «Справжнє» значення B може бути навіть просто значенням необроблених тварин, елементів управління (C).

Відмова від нульової гіпотези

В принципі, вчений розробляє експеримент, щоб спростувати чи ні, що спостережуваний ефект обумовлений лише випадковістю. Це називається відкиданням нульової гіпотези.

Значення p - це ймовірність того, що немає різниці між експериментальним і контрольним; тобто, що нульова гіпотеза правильна. Так що якщо ймовірність того, що експериментальне середнє відрізняється від контрольного середнього більше 0,05, то різниця зазвичай не вважається істотною. Якщо p = <0,05, різниця вважається значною, а нульова гіпотеза відхиляється.

У нашому гіпотетичному прикладі різниця між експериментальною групою A та елементами управління (C) виявляється значною; що між B та елементами управління немає.

Звуження меж довіри

Можна використовувати два підходи, щоб звузити межі довіри.

збільшити розмір вимірюваного зразка (збільшується n)
знайти способи зменшити коливання вимірювань про середнє значення.

Друга мета часто набагато складніше досягти; якщо вона виявиться неможливою, можливо, нульова гіпотеза все-таки є правильною!