Skip to main content
LibreTexts - Ukrayinska

6.3: Зв'язування ліганду

  1. Last updated
  2. Save as PDF
  • Page ID
    7412

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Молекулярне розпізнавання є ключовим аспектом практично всієї біохімії і передбачає:

    • Реплікація ДНК
    • Генна регуляція
    • Транскрипція ДНК в мРНК
    • Переклад мРНК в білки
    • Функція ферменту
    • Молекулярна збірка
    • Трансдукція сигналу
    • Клітинно-клітинний зв'язок
    • Імунологія

    Міжмолекулярні взаємодії, в найпростішому прикладі, включають дві молекули, які розпізнають і зв'язуються один з одним:

    • ліганд
    • рецептор

    Це широкі терміни, але загальні властивості рецептора і ліганду такі:

    • Ліганд, як правило, є невеликою молекулою, і він дифундує по всьому навколишньому середовищу, поки не зв'язується з певним рецептором
    • Рецептор, як правило, являє собою велику, відносно стаціонарну молекулу, яка містить специфічне місце зв'язування ліганду. При зв'язуванні ліганду структурні та/або хімічні властивості рецептора зазвичай змінюються

    Взаємодія між рецептором і лігандом, як правило, не ковалентна

    • Існує загальна молекулярна комплементарність між рецептором і лігандом.
    • Часто, але не завжди, існує ентропна вартість, пов'язана з зв'язуванням ліганду з рецептором, але це з лишком компенсується сприятливою ентальпією (тобто молекулярною компліментарністю)
    • Енергія зв'язування, як правило, використовується, щоб викликати структурні зміни, пов'язані з подією молекулярного зв'язку.

    Існує два загальні методи дослідження взаємодій рецепторів/лігандів:

      1. Рівноважна термодинаміка, і
      2. Кінетика асоціації та дисоціації

    Аналіз рівноважного зв'язування ліган/рецепторів

    Два можливих стану взаємодії ліга/рецепторів та константи швидкості, пов'язані з їх утворенням, наведені як:

    захоплення 6.PNG

    Константа рівноваги асоціації (освіти), K f, задається як:

    захоплення 8.PNG

    • [RL] - концентрація комплексу, [R] - концентрація вільного R при рівновазі, а [L] - концентрація вільного L при рівновазі
    • K f має одиниці М -1
    • Велике значення для K f означає, що рівновага сприяє комплексу - спостерігається висока спорідненість рецептора до ліганду
    • Невелике значення для K f означає, що рівновага сприяє поділу рецептора і ліганду, а рецептор має низьку спорідненість до ліганду.

    Просто для того, щоб ускладнити життя, типовою рамкою відліку при описі спорідненості рецепторів до ліганду є посилання на константу дисоціації, K d:

    Capture5.PNG

    • K d має одиниці М
    • Невелике значення для K d означає, що рівновага сприяє комплексу - спостерігається висока спорідненість рецептора до ліганду
    • Велике значення для K d означає, що рівновага сприяє поділу рецептора і ліганду, а рецептор має низьку спорідненість до ліганду

    При рівновазі швидкість утворення комплексу RL дорівнює швидкості дисоціації:

    Capture.PNG

    Лівий вираз - це визначення константи дисоціації, K d, отже:

    capture1.PNG

    Вираз вільної енергії і K f і K d

    З початкового вираження складного освіти:

    Capture2.PNG

    Стандартна зміна вільної енергії стану, Δ G 0, для процесу (тобто починаючи з 1M все) буде дано як:

    Capture3.PNG

    Оскільки K d - обернене K f:

    capture4.PNG

    У цьому випадку від'ємне значення для DG 0 (що вказує на спонтанність) виникне, коли K d < 1,0. Це станеться, коли є висока спорідненість і рівновага сприяє складному утворенню.

    Практичні зв'язки між [R], [L], K d і [RL]

    При однаковій концентрації доданого ліганду і рецептора буде відбуватися більш складне утворення при меншому значенні K d

    Приклад 6.3.1

    Рецептор і ліганд додають до загальної концентрації 1,0 х 10 -4 М. K d для комплексу RL становить 1,0 х 10 -4 М. Яка концентрація [R], [L] і [RL] при рівновазі?

    Знімок екрана (429) .png

    Доданий ліганд, L, буде розділений між вільною та зв'язаною формами:

    L всього = Л + РЛ = 1,0 х 10 -4 М

    Д = 1,0 х 10 -4 М - РЛ

    Аналогічно, доданий рецептор, R, буде розділений між вільною та пов'язаною формами:

    R всього = R + RL = 1,0 х 10 -4 М

    R = 1,0 х 10 -4 М - РЛ

    Підстановка цих значень L і R у вираз для K d дає:

    Скріншот (430) .png

    Це квадратика зі значеннями a = 1, b = -3,0 х 10 -4 і c = 1,0 х 10 -8. Це дає два можливі значення для RL:

    RL = 2,62 Х 10 -4 М або

    РЛ = 3,82 Х 10 -5

    Оскільки максимально можливе значення для [RL] становить 1,0 х 10 -4 (тобто, враховуючи початкові концентрації R і L, це найбільша кількість RL, яка може бути сформована), перший результат неможливий і [RL] = 3,82 X 10 -5 M

    Так, 38,2% доданого рецептора знаходиться в комплексоутворенні (тобто 3,82 Х 10 -5 М/1,0 х 10 -4) х 100%

    Приклад 6.3.2

    Така ж кількість доданих R і L, але на цей раз K d для комплексу RL становить 1,0 х 10 -6 М. Яка концентрація [R], [L] і [RL] при рівновазі?

    Знімок екрана (431) .png

    це квадратика зі значеннями a = 1, b = -2,01 х 10 -4 і c = 1,0 х 10 -8. Це дає два можливі значення для RL:

    RL = 1,11 Х 10 -4 М або

    РЛ = 9,05 Х 10 -5

    Оскільки максимально можливе значення для [RL] становить 1,0 х 10 -4 (тобто, враховуючи початкові концентрації R і L, це найбільша кількість RL, яка може бути сформована), перший результат неможливий і [RL] = 9,05 X 10 -5 M

    Так, 90,5% доданого рецептора знаходиться в комплексоутворенні (тобто 9,05 Х 10 -5 М/1,0 х 10 -4) х 100%

    При однаковій концентрації доданого ліганду і рецептора буде відбуватися більш складне утворення при меншому значенні K d

    Визначення констант дисоціації (K d) або зв'язування (K f)

    Співвідношення між K d, [R], [L] і [RL] задається:

    захоплення 9.PNG

    • Це рівняння з чотирма змінними, якщо ви знаєте три з них, ви можете вирішити для четвертої
    • В принципі, ви можете вирішити для K d, якщо ви знаєте концентрацію вільного рецептора [R], вільного ліганду [L] і рецептора/лігандного комплексу [RL] при рівновазі

    Щоб мати можливість вирішити для K d, вам потрібен аналіз, який забезпечить молярні концентрації для кожного компонента. Однак цього, як правило, важко досягти. Набагато частіше є аналіз, який надасть вам інформацію щодо частки доданого рецептора (або ліганду), який присутній у вільній або складній формі.

    • Якщо [R t] - загальна концентрація рецептора в зразку, ми знаємо, що він буде розділений на дві популяції - зв'язані і вільні:

    Capture10.PNG

    • Фракція пов'язаних рецепторних сайтів задається співвідношенням:


    Capture11.PNG

    • Фракція зв'язаних рецепторів відома змінною a, а має значення від 0 до 1

    Захоплення 12.PNG

    • Підставляючи значення на [R t] в терміні [R] та [RL], наведених вище, дає:

    Capture13.PNG

    • Зв'язок між [RL] і K d задається виразом для Kd:

    Capture14.PNG

    • Цей вираз для [RL] можна підставити у вираз для a to yield:

    Capture15.PNG

    • Спростіть, попередньо розділивши через [R]:

    Capture16.PNG

    • Потім множимо на K d:

    Захоплення 17.PNG

    Це рівняння має три змінні:

    1. Концентрація вільного ліганду при рівновазі [L]
    2. Константа дисоціації, K d, для комплексу RL
    3. Фракція рецептора, яка знаходиться в зв'язаній формі при рівновазі, а

    Якщо ви знаєте дві з цих змінних, ви можете вирішити для третьої (тобто якщо експериментальний аналіз кількісно [L] і a, ви можете вирішити для K d)

    Вищевказаним рівнянням можна маніпулювати далі шляхом підстановки значення a через [RL] і [R t]:

    Capture18.PNG

    Це рівняння має чотири змінні:

    1. Концентрація вільного ліганду при рівновазі [L]
    2. Константа дисоціації, K d, для комплексу RL
    3. Концентрація рецептора, що знаходиться в зв'язаній формі при рівновазі [RL]
    4. Загальна концентрація рецептора в зразку

    Зазвичай експеримент з зв'язування лігандів налаштований таким чином, що [Rt] тримається постійною, а [RL] контролюється як функція [L]

    Це рівняння дуже схоже на рівняння Міхаеліса-Ментена:

    Capture19.PNG

    Побудова V проти [S] в рівнянні М-М дає прямокутну гіперболу. Таким чином, побудова графіка [RL] проти [L] також дасть прямокутну гіперболу

    • Асимптота кривої дасть значення [R t]
    • Концентрація вільного ліганду [L], що призводить до половини максимального значення [RL], дорівнює значенню K d

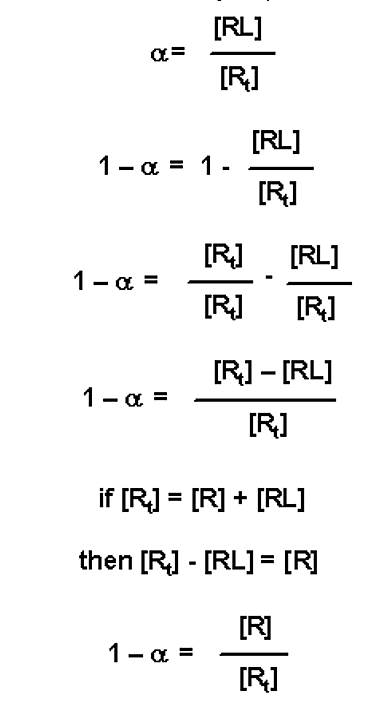
    Ще одна модифікація полягає в тому, щоб зрозуміти, що якщо a дорівнює частці рецептора, пов'язаного в комплексі (зі значенням 0 ≤ α ≤ 1,0), то (1 - α) є часткою вільного рецептора (тобто фракції незв'язаного рецептора)

    Знімок екрана (432) .png

    Це значення можна підставити в три змінні вирази вище:

    Знімок екрана (433) .png

    Це рівняння має чотири змінні:

    1. Концентрація вільного ліганду при рівновазі [L]
    2. Константа дисоціації, K d, для комплексу RL
    3. Концентрація рецептора, що знаходиться у вільній формі при рівновазі [R]
    4. Загальна концентрація рецептора в зразку [R t]

    Зазвичай експеримент з зв'язування лігандів налаштований таким чином, що [Rt] тримається постійною, а [R] контролюється як функція [L]

    (Примітка: Хоча це виглядає як рівняння М-М, K d є постійною.)

    Наведені вище похідні називаються "зв'язуючими ізотермами" у зв'язку з їх здатністю вирішувати для Kd в умовах рівноваги (і вихідне рівноважне термодинамічне рівняння використовується постійна температура)

    Знімок екрана (434) .png

    Побудова даних для різних значень [L], [R t], і або [RL] або [R], і підгонка до відповідної функції вище, дозволяє більш точно визначити K d (хоча один експеримент дасть відповідь).

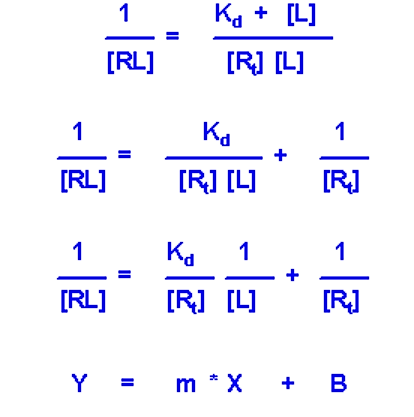
    Через схожість графіка [RL] проти [L] з графіком М-М, це часто є більш бажаною експериментальною установкою. Зокрема, для більш точного визначення K d може бути використаний подвійно-зворотний графік (так само, як і двозворотний М-М графік)

    Знімок екрана (435) .png

    • Якщо ви намалюєте 1/ [RL] проти 1/ [L], ви отримаєте пряму лінію, нахил якої дорівнює K d/[R t]
    • Перехоплення Y буде дорівнює 1/ [R t]. Оскільки це значення фіксоване і відоме, значення перехоплення y може служити перевіркою, щоб переконатися, що експеримент відповідає моделі

    Експеримент рівноважного діалізу

    Напівпроникна мембрана може бути використана в експерименті з рівноваги на основі діалізу для визначення Kd для пари ліганд-рецепторів.

    • Мембрана повинна бути вільно проникною, що стосується ліганду (зазвичай це невелика молекула), але представляти бар'єр для рецептора
    • Експеримент встановлюється з відомою концентрацією рецептора з одного боку, а відомою концентрацією ліганду - з іншого
    • Системі дозволено прийти до рівноваги
    • Експеримент вимагає проведення аналізу на ліганд

    Знімок екрана (436) .png

    Малюнок 6.3.1: Напівпроникний бар'єр

    Після досягнення рівноваги оцінюють концентрацію ліганду по обидва боки напівпроникної мембрани:

    Знімок екрана (438) .png

    Малюнок 6.3.2: Концентрація рівнова

    Capture20.PNG

    • Оскільки ліганд не впливає на мембрану, концентрація ліганду на стороні без рецептора дорівнює концентрації вільного ліганду [L] скрізь у зразку (тобто по обидва боки мембрани)
    • Концентрація ліганду буде дорівнює концентрації вільного ліганду [L] плюс ліганд, присутній в рецепторному комплексі [RL] (іншими словами, повинна бути більша концентрація ліганду на стороні з рецептором, якщо рецептор має спорідненість до ліганду)
    • Концентрацію рецептор/лігандного комплексу [RL] можна визначити за різницею між цими двома значеннями
    • Загальна концентрація рецепторів - відома величина (експериментатор визначається на початку експерименту, і не змінюється)
    • Будь-яка ізотерма зв'язування може бути використана для вирішення для K d (оскільки [R] також може бути визначено)