3.4: Конститутивні відносини

Вступ

Модулі з кінематики (Модуль 8), рівноваги (Модуль 9) та тензорних перетворень (Модуль 10) містять поняття життєво важливі для механіки матеріалів, але вони не дають уявлення про роль самого матеріалу. Кінематичні рівняння пов'язують деформації з градієнтами переміщення, а рівняння рівноваги пов'язують напругу з застосованими тягами на навантажених границях, а також регулюють відносини між градієнтами напружень всередині матеріалу. У трьох вимірах є шість кінематичних рівнянь і три рівняння рівняння рівняння рівняння, загалом дев'ять. Однак існує п'ятнадцять змінних: три зміщення, шість деформацій і шість напружень. Нам потрібно ще шість рівнянь, і вони забезпечуються конститутивними відносинами матеріалу: шістьма виразами, що стосуються напружень до деформацій. Це свого роду механічне рівняння стану, і описують, як матеріал складається механічно.

За допомогою цих конститутивних відносин підтверджується життєва роль матеріалу: пружні константи, що з'являються в цьому модулі, є властивостями матеріалу, підлягають контролю шляхом обробки та мікроструктурної модифікації, як зазначено в Модулі 2. Це важливий інструмент для інженера, і вказує на необхідність розгляду дизайну матеріалу, а також матеріалу.

Ізотропні еластичні матеріали

У загальному випадку лінійного співвідношення між компонентами тензорів деформації та напружень можна запропонувати твердження виду

\[\epsilon_{ij} = S_{ijkl} \sigma_{kl}\nonumber\]

де\(S_{ijkl}\) є тензор четвертого рангу. Це являє собою послідовність з дев'яти рівнянь, так як кожен компонент\(\epsilon_{ij}\) являє собою лінійну комбінацію всіх складових\(\sigma_{ij}\). Наприклад:

\[\epsilon_{23} = S_{2311} \sigma_{11} + S_{2312} \sigma_{12} + \cdots + S_{2333} \epsilon_{33}\nonumber\]

Виходячи з кожного з індексів\(S_{ijkl}\) прийняття значень від 1 до 3, ми могли б очікувати в цілому 81 незалежних компонентів в\(S\). Однак обидва\(\epsilon_{ij}\) і\(\sigma_{ij}\) симетричні, з шістьма, а не дев'ятьма незалежними компонентами кожен. Це зменшує кількість\(S\) компонентів до 36, як видно з лінійного співвідношення між псевдовекторними формами деформації і напруження:

\[\left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right \} = \begin{bmatrix} S_{11} & S_{12} & \cdots & S_{16} \\ S_{21} & S_{22} & \cdots & S_{26} \\ \cdots & \cdots & \cdots & \cdots \\ S_{61} & S_{62} & \cdots & S_{66} \end{bmatrix} \left \{ \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \tau_{yz} \\ \tau_{xz} \\ \tau_{xy} \end{matrix} \right \}\]

Можна показати (Г.М. Мазе, Схеми теорії та проблем механіки суцільних середовищ Шаума, McGraw-Hill, 1970.), що\(S\) матриця в такому вигляді також симетрична. Тому він містить лише 21 незалежний елемент, що видно, підраховуючи елементи у верхньому прямокутному трикутнику матриці, включаючи діагональні елементи (1 + 2 + 3 + 4 + 5 + 6 = 21).

Якщо матеріал проявляє симетрію в своїй пружній реакції, кількість незалежних елементів в\(S\) матриці може бути зменшено ще далі. У найпростішому випадку ізотропного матеріалу, жорсткості якого однакові у всіх напрямках, незалежними є тільки два елементи. Раніше було показано, що в двох вимірах співвідношення між деформаціями і напруженнями в ізотропних матеріалах можна записати як

\[\begin{array} {c} {\epsilon_x = \dfrac{1}{E} (\sigma_x - \nu \sigma_y)} \\ {\epsilon_y = \dfrac{1}{E} (\sigma_y - \nu \sigma_x)} \\ {\gamma_{xy} = \dfrac{1}{G} \tau_{xy}} \end{array}\]

разом із співвідношенням

\[G = \dfrac{E}{2(1 + \nu)}\nonumber\]

Розширюючи це до трьох вимірів, псевдовекторно-матрична форма рівняння 3.4.1 для ізотропних мат-ріалів становить

\[\left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right \} = \begin{bmatrix} \tfrac{1}{E} & \tfrac{-\nu}{E} & \tfrac{-\nu}{E} & 0 & 0 & 0 \\ \tfrac{-\nu}{E} & \tfrac{1}{E} & \tfrac{-\nu}{E} & 0 & 0 & 0 \\ \tfrac{-\nu}{E} & \tfrac{-\nu}{E} & \tfrac{1}{E} & 0 & 0 & 0 \\ 0 & 0 & 0 & \tfrac{1}{G} & 0 & 0 \\ 0 & 0 & 0 & 0 & \tfrac{1}{G} & 0 \\ 0 & 0 & 0 & 0& 0 & \tfrac{1}{G} \end{bmatrix} \left \{ \begin{matrix} \sigma_x \\ \sigma_y \\ \sigma_z \\ \tau_{yz} \\ \tau_{xz} \\ \tau_{xy} \end{matrix} \right \}\]

Величина в дужках називається матрицею відповідності матеріалу, позначається\(S\) або\(S_{ij}\). Важливо зрозуміти фізичну значимість різних його термінів. Безпосередньо з правил множення матриці елемент в\(i^{th}\) рядку і\(j^{th}\) стовпці\(S_{ij}\) - це внесок\(j^{th}\) напруги в\(i^{th}\) деформацію. Наприклад, компонент у положенні 1,2 є внеском напруги -напрямку до деформації\(y\) -напрямку:\(\sigma_y\) множення на\(1/E\) дає деформацію\(x\) -direction, породжену\(\sigma_y\), а потім множення цього на\(-\nu\) дає деформацію Пуассона\(y\) індукований в\(x\) напрямку. Нульові елементи показують відсутність зчеплення між нормальними та зсувними компонентами.

Ізотропний конститутивний закон також може бути записаний, використовуючи індексні позначення як (див. Вправа\(\PageIndex{1}\))

\[\epsilon_{ij} = \dfrac{1 + \nu}{E} \sigma_{ij} - \dfrac{\nu}{E} \delta_{ij} \sigma_{kk}\]

де тут використовується індиціальна форма деформації і\(G\) була усунена за допомогою\(G = E/2(1 + \nu)\) Символу\(\delta_{ij}\) є дельта Кроенеккера, описана в модулі матриці та позначеннях індексу.

Якщо ми хочемо записати напруження через деформації, Eqn 3.4.3 можна інвертувати. У випадках плоского напруження (\(\sigma_z = \tau_{xz} = \tau_{yz} = 0\)) це дає

\[\left \{ \begin{matrix} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{matrix} \right \} = \dfrac{E}{1-\nu^2} \begin{bmatrix} 1 & \nu & 0 \\ \nu & 1 & 0 \\ 0 & 0 & (1 - \nu)/2 \end{bmatrix} \left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \gamma_{xy} \end{matrix} \right \}\]

де знову\(G\) був замінений\(E/2(1 + \nu)\). Або, в скороченому позначенні:

\[\sigma = D \epsilon\]

де\(D = S^{-1}\) - матриця жорсткості.

Гідростатичні та спотворювальні компоненти

Малюнок 1: Гідростатичне стиснення.

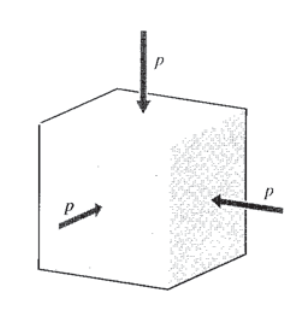
Стан гідростатичного стиснення, зображене на малюнку 1, - це таке, при якому не існує напружень зсуву і де всі нормальні напруги рівні гідростатичному тиску:

\[\sigma_x = \sigma_y = \sigma_z = -p\nonumber\]

де знак мінус вказує на те, що стиснення умовно позитивне для тиску, а негативне для стресу. Для цього стресового стану очевидно, що

\[\dfrac{1}{3} (\sigma_x + \sigma_y + \sigma_z) = \dfrac{1}{3} \sigma_{kk} = -p\nonumber\]

так що гідростатичний тиск є негативним середнім нормальним напруженням. Ця величина становить лише третину інваріанта напруги\(I_1\), що є відображенням гідростатичного тиску, однакового у всіх напрямках, не змінюючись при обертанні осі.

У багатьох випадках, крім прямого гідростатичного стиснення, все ж зручно «дисоціювати» гідростатичний (або «дилатаційний») компонент від тензора напружень:

\[\sigma_{ij} = \dfrac{1}{3} \sigma_{kk} \delta_{ij} + \sum_{ij}\]

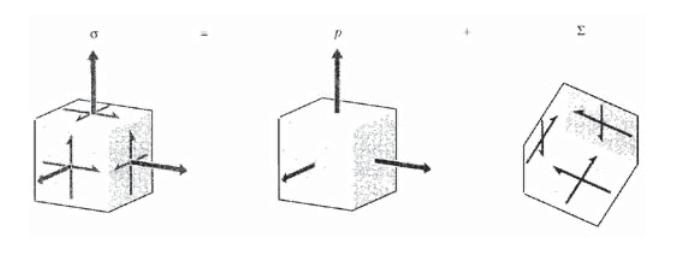
\(\sum_{ij}\)Ось що залишилося\(\sigma_{ij}\) після віднімання гідростатичної складової. \(\sum_{ij}\)Тензор може бути показаний як стан чистого зсуву, тобто існує перетворення осі таким чином, що всі нормальні напруги зникають (див. Вправа\(\PageIndex{5}\)). The\(\sum_{ij}\) називається спотвореної, або девіаторичної, складовою напруги. Отже, всі стресові стани можна вважати двома складовими, як показано на малюнку 2, один суто розширювальний і один чисто спотворений. Ця концепція зручна тим, що матеріал реагує на ці компоненти напруги дуже по-різному. Наприклад, пластичний і в'язкий потік переважають спотвореними компонентами, при цьому гідростатична складова викликає лише пружні деформації.

Малюнок 2: Дилатаційна і девіаторна складові тензора напружень.

Приклад\(\PageIndex{1}\)

Розглянемо стресовий стан

\[\sigma = \begin{bmatrix} 5 & 6 & 7 \\ 6 & 8 & 9 \\ 7 & 9 & 2 \end{bmatrix}, \text{ GPa} \nonumber\]

Середнє нормальне напруження є\(\sigma_{kk}/3 = (5 + 8 + 2)/3 = 5\), тому напруження розкладання є

\[\sigma = \dfrac{1}{3} \sigma_{kk} \delta_{ij} + \sum_{ij} = \begin{bmatrix} 5 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 5 \end{bmatrix} + \begin{bmatrix} 0 & 6 & 7 \\ 6 & 3 & 9 \\ 7 & 9 & -3 \end{bmatrix}\nonumber\]

Неочевидно, що девіаторна складова, наведена у другій матриці, являє собою чистий зсув, оскільки на її діагоналі є ненульові складові. Однак перетворення напруги за допомогою кутів Ейлера\(\psi = \phi = 0, \theta = -9.22^{\circ}\) дає напружений стан

\[\sum' = \begin{bmatrix} 0.00 & 4.80 & 7.87 \\ 4.80 & 0.00 & 9.49 \\ 7.87 & 9.49 & 0.00 \end{bmatrix}\nonumber\]

Гідростатична складова напружень пов'язана з об'ємною деформацією через модуль стисливості (\(-p = K \Delta V/V\)), тому

\[\dfrac{1}{3} \sigma_{kk} = K\epsilon_{kk}\]

Подібно до стресу, штам також може бути дисоційований як

\[\epsilon_{ij} = \dfrac{1}{3} \epsilon_{kk} \delta_{ij} + e_{ij}\nonumber\]

де\(e_{ij}\) - девіаторний компонент штаму. Девіаторні компоненти напруги та деформації пов'язані модулем зсуву матеріалу:

\[\sum_{ij} = 2Ge_{ij}\]

де необхідний коефіцієнт 2, оскільки тензорні описи штаму - це половина класичних штамів, для яких\(G\) були табличні значення. Написання складових рівнянь у вигляді Eqns. 3.4.8 і 3.4.9 дає просту форму без зв'язкових термінів в умовному\(E-\nu\) вигляді.

Приклад\(\PageIndex{2}\)

Використовуючи напружений стан попереднього прикладу разом з пружними константами для сталі (\(E = 207\)ГПа,\(K = E/3(1 - 2\nu) = 173\) ГПа\(\nu = 0.3\),\(G = E/2(1 + \nu) = 79.6\) ГПа), дилатаційні та спотворення складові деформації наведено

\[\delta_{ij} \epsilon_{kk} = \dfrac{\delta_{ij} \sigma_kk}{3K} = \begin{bmatrix} 0.0289 & 0 & 0 \\ 0 & 0.0289 & 0 \\ 0 & 0 & 0.0289 \end{bmatrix}\nonumber\]

\[e_{ij} = \dfrac{\sum_{ij}}{2G} = \begin{bmatrix} 0 & 0.0378 & 0.0441 \\ 0.0378 & 0.0189 & 0.0567 \\ 0.0441 & 0.0567 & -0.0189 \end{bmatrix}\nonumber\]

Загальна деформація тоді

\[\epsilon_{ij} = \dfrac{1}{3} \epsilon_{kk} \delta_{ij} + e_{ij} = \begin{bmatrix} 0.00960 & 0.0378 & 0.0441 \\ 0.0378 & 0.0285 & 0.0567 \\ 0.0441 & 0.0567 & -0.00930 \end{bmatrix}\nonumber\]

Якщо оцінити загальну деформацію за допомогою рівняння 3.4.4, ми маємо

\ (\ epsilon_ {ij} =\ drac {1 +\ nu} {E}\ sigma_ij -\ drac {\ nu} {E}\ delta_ {ij}\ сигма_ {кк} =\ почати {bmatrix} 0,00965 & 0.0377 & 0.0440\ 0.0377 & 0.0285 & 0.0565\ 0.0440 & 0,0377 & -0.00915\ кінець {bmatrix}\ nonumber\]

Ці результати однакові, відрізняються лише похибкою округлення.

Модель скінченного деформації

Коли деформації стають великими, можуть виникнути геометричні, а також матеріальні нелінійності, які важливі для багатьох практичних завдань. У цих випадках аналітик повинен використовувати не тільки іншу міру деформації, наприклад, деформацію Лагранжа, описану в Модулі 8, але й різні заходи напруги («Другий стрес Піола-Кіршофа» замінює стрес Коші, коли використовується деформація Лагранжа) та різні складові закони стрес-деформації. Обробка цих формулювань виходить за рамки цих модулів, але тут буде викладена проста нелінійна модель напружено-деформованих матеріалів для гумових матеріалів, щоб проілюструвати деякі аспекти аналізу скінченних деформацій. Текст від Bath (К.-Дж. Bathe, Процедури скінченних елементів в інженерному аналізі, Prentice-Hall, 1982.) забезпечує більш широке обговорення цієї області, включаючи реалізацію кінцевих елементів.

У разі невеликих переміщень деформація\(\epsilon_x\) задається виразом:

\[\epsilon_x = \dfrac{1}{E} [\sigma_x - \nu (\sigma_y + \sigma_z)]\nonumber\]

Для випадку еластомерів з\(\nu = 0.5\), це може бути переписано з точки зору середнього напруження\(\sigma_m = (\sigma_x + \sigma_y + \sigma_z)/3\) як:

\[2 \epsilon_x = \dfrac{3}{E} (\sigma_x - \sigma_m)\nonumber\]

Для великодеформованого випадку запропоновано наступне аналогічне співвідношення напруження-деформація:

\[\lambda_x^2 = 1 + 2 \epsilon_x = \dfrac{3}{E} (\sigma_x - \sigma_m^*)\]

де тут\(\epsilon_x\) знаходиться штам Лагранжа і\(\sigma_m^*\) є параметром, необов'язково рівним\(\sigma_m\). \(\sigma_m^*\)Параметр можна знайти для випадку одновісного натягу, розглянувши поперечні скорочення\(\lambda_y = \lambda_z\):

\[\lambda_y^2 = \dfrac{3}{E} (\sigma_y - \sigma_m^*)\nonumber\]

Так як для гуми\(\lambda_x \lambda_y \lambda_z = 1\),\(\lambda_y^2 = 1/\lambda_x\). Здійснення цієї заміни та вирішення для\(\sigma_m^*\):

\[\sigma_m^* = \dfrac{-E\lambda_y^2}{3} = \dfrac{-E}{3\lambda_x}\nonumber\]

Підставляючи це назад у рівняння 3.4.10,

\[\lambda_x^2 = \dfrac{E}{3} (\sigma_x - \dfrac{E}{3\lambda_x})\nonumber\]

Рішення для\(\sigma_x\),

\[\sigma_x = \dfrac{E}{3} (\lambda_x^2 - \dfrac{1}{\lambda_x})\nonumber\]

Тут напруга\(\sigma_x = F/A\) - це «справжнє» напруження, засноване на фактичній (скороченій) площі поперечного перерізу. «Інженерне» напруження,\(\sigma_e = F/A_0\) засноване на вихідній площі\(A_0 = A \lambda_x\), становить:

\[\sigma_e = \dfrac{\sigma_x}{\lambda_x} = G\left (\lambda_x - \dfrac{1}{\lambda_x^2} \right )\nonumber\]

де\(G = E/2(1 + \nu) = E/3\) для\(\nu = 1/2\). Цей результат такий же, як і отриманий у модулі 2, враховуючи силу, що виникає внаслідок зниженої ентропії, оскільки молекулярні сегменти, що охоплюють ділянки зшивання, розширюються. Це з'являється тут з простої гіпотези стрес-деформованої реакції, використовуючи відповідну міру скінченної деформації.

анізотропні матеріали

Малюнок 3: Ортотропний матеріал.

Якщо матеріал має текстуру, таку як дерево або однонаправлено армовані волокнисті композити, як показано на малюнку 3, модуль пружності\(E_1\) у напрямку волокна, як правило, буде більшим, ніж у поперечних напрямках (\(E_2\)і\(E_3\)). Коли\(E_1 \ne E_2 \ne E_3\), матеріал, як кажуть, ортотропний. Однак загальним є те, що властивості в площині, поперечній до напрямку волокна, щоб бути ізотропними до хорошого наближення\((E_2 = E_3)\); такий матеріал називається поперечно-ізотропним. Пружні конститутивні закони повинні бути змінені з урахуванням цієї анізотропії, а наступна форма є продовженням рівняння 3.4.3 для поперечно-ізотропних матеріалів:

\[\left \{ \begin{matrix} \epsilon_1 & \epsilon_2 & \gamma_{12} \end{matrix} \right \} = \begin{bmatrix} 1/E_1 & -\nu_{21}/E_2 & 0 \\ -\nu_{12}/E_1 & 1/E_2 & 0 \\ 0 & 0 & 1/G_{12} \end{bmatrix} \left \{ \begin{matrix} \sigma_1 & \sigma_2 & \tau_{12} \end{matrix} \right \}\]

Параметр\(\nu_{12}\) є основним коефіцієнтом Пуассона; це відношення деформації, індукованої у напрямку 2 деформацією, застосованою в 1-напрямку. Цей параметр не обмежується значеннями менше 0,5, як в ізотропних матеріалах. І навпаки,\(\nu_{21}\) дає деформацію, індуковану в 1-напрямку деформацією, застосованою у напрямку 2. Оскільки 2-напрямок (поперечний до волокон) зазвичай має набагато меншу жорсткість, ніж 1-напрямок, повинно бути зрозуміло, що дана деформація в напрямку 1 зазвичай розвиває набагато більшу деформацію в напрямку 2, ніж буде така ж деформація в напрямку 2 індукує деформацію в напрямку 1. Отже, ми зазвичай матимемо\(\nu_{12} > \nu_{21}\). У наведеному вище рівнянні (\(E_1, E_2, \nu_{12}, \nu_{21}\)і\(G_{12}\)) є п'ять констант. Однак тільки чотири з них незалежні; так як\(S\) матриця симетрична,\(\nu_{21}/E2 = \nu_{12}/E1\).

Таблицю пружних констант та інших властивостей для широко використовуваних анізотропних матеріалів можна знайти в Модулі властивостей композитного шару.

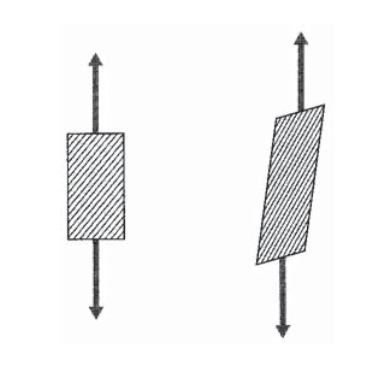
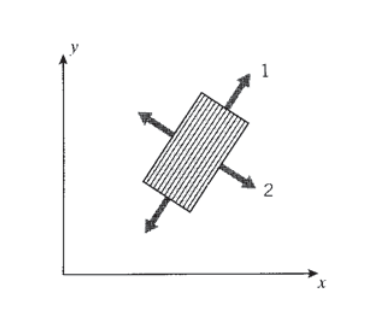
Проста форма Рівняння 3.4.11, з нулями в термінами, що представляють зв'язок між нормальною і зсувною складовими, виходить тільки тоді, коли осі вирівняні по основним напрямкам матеріалу; тобто уздовж і поперечно до осей волокон. Якщо осі орієнтовані по якомусь іншому напрямку, всі терміни матриці відповідності будуть заповнені, і симетрія матеріалу не буде кидатися в очі. Якщо, наприклад, напрямок волокна знаходиться поза віссю від напрямку завантаження, матеріал буде розвивати деформацію зсуву, коли волокна намагаються зорієнтуватися вздовж напрямку навантаження, як показано на малюнку 4. Тому буде зв'язок між нормальним напруженням і деформацією зсуву, яка ніколи не відбувається в ізотропному матеріалі.

Малюнок 4: Зсуво-нормальна муфта.

Закон трансформації для відповідності може бути розроблений з законів трансформації деформацій і напружень, використовуючи процедури, описані в Модулі 10 (Трансформації). Послідовними перетвореннями псевдовекторна форма для деформації в\(x-y\) довільному напрямку, показана на малюнку 5, пов'язана з деформацією в 1-2 (основний матеріал) напрямках, потім з напруженнями в 1-2 напрямках і, нарешті, до напружень в\(x-y\) напрямках. Остаточною групуванням матриць перетворення, що стосуються\(x-y\) деформацій до\(x-y\) напружень, є перетворена матриця відповідності в\(x-y\) напрямку:

Малюнок 5: Перетворення осі для складових рівнянь.

\[\left \{ \begin{matrix} \epsilon_x & \epsilon_y & \gamma_{xy} \end{matrix} \right \} = R \left \{ \begin{matrix} \epsilon_x & \epsilon_y & \tfrac{1}{2} \gamma_{xy} \end{matrix} \right \} = RA^{-1} \left \{ \begin{matrix} \epsilon_1 & \epsilon_2 & \tfrac{1}{2} \gamma_{12} \end{matrix} \right \} = RA^{-1}R^{-1} \left \{ \begin{matrix} \epsilon_1 & \epsilon_2 & \gamma_{12} \end{matrix} \right \}\nonumber\]

\[=RA^{-1}R^{-1} S \left \{ \begin{matrix} \sigma_1 & \sigma_2 & \tau_{12} \end{matrix} \right \} = RA^{-1}RSA \left \{ \begin{matrix} \sigma_x & \sigma_y & \sigma_{xy} \end{matrix} \right \} = \bar{S} \left \{ \begin{matrix} \sigma_x & \sigma_y & \sigma_{xy} \end{matrix} \right \}\nonumber\]

де\(\bar{S}\) - перетворена матриця відповідності щодо\(x-y\) осей. \(A\)Ось матриця перетворення, і\(R\) матриця Рейтера, визначена в Модулі тензорних перетворень. Зворотний від\(\bar{S}\) is\(\bar{D}\), матриця жорсткості щодо\(x-y\) осей:

\[\bar{S} = RA^{-1}SA, \ \ \bar{D} = \bar{S}^{-1}\]

Приклад\(\PageIndex{1}\)

Розглянемо шар кевлар-епоксидного композиту з жорсткістю\(E_1 = 82, E_2 = 4, G_{12} = 2.8\) (всі ГПа) і\(\nu_{12} = 0.25\). Матриця відповідності\(S\) в напрямку 1-2 (матеріал) становить:

\[S = \begin{bmatrix} 1/E_1 & -\nu_{21} /E_2 & 0 \\ -\nu_{12} /E_1 & 1/E_2 & 0 \\ 0 & 0 & 1/G_{12} \end{bmatrix} = \begin{bmatrix} .1220 \times 10^{-10} & -.3050 \times 10^{-11} & 0 \\ -.3050 \times 10^{-11} & .2500 \times 10^{-9} & 0 \\ 0 & 0 & .3571 \times 10^{-9} \end{bmatrix}\nonumber\]

Якщо шар орієнтований на напрямок волокна (напрямок «1")\(\theta = 30^{\circ}\) від\(x-y\) осей, відповідна матриця перетворення

\[A = \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} = \begin{bmatrix} .7500 & .2500 & .8660 \\ .2500 & .7500 & -.8600 \\ -.4330 & .4330 & .5000 \end{bmatrix}\nonumber\]

Матриця відповідності щодо\(x-y\) осей тоді

\[\bar{S} = RA^{-1}R^{-1}SA = \begin{bmatrix} .8830 \times 10^{-10} & -.1970 \times 10^{-10} & -1.222 \times 10^{-9} \\ -.1971 \times 10^{-10} & .2072 \times 10^{-9} & -.8371 \times 10^{-10} \\ 1.222 \times 10^{-9} & -.8369 \times 10^{-10} & -2905 \times 10^{-9} \end{bmatrix}\nonumber\]

Зауважте, що ця матриця є симетричною (до числової помилки округлення), але існують ненульові значення зв'язку. Користувач, який не знає про внутрішній склад матеріалу, вважав би його повністю анізотропним.

Очевидні інженерні константи, які спостерігалися б, якби шар був випробуваний в,\(x-y\) а не в 1-2 напрямках, можна знайти безпосередньо з перетвореної\(\bar{S}\) матриці. Наприклад, видимий модуль пружності в\(x\) напрямку дорівнює\(E_x = 1/\bar{S}_{1,1} = 1/(.8830 \times 10^{-10} = 11.33\) ГПа.

Вправа\(\PageIndex{1}\)

Розгорніть індиціальні форми керівних рівнянь твердої пружності в трьох вимірах:

\[\text{equilibrium: } \sigma_{ij,j} = 0\nonumber\]

\[\text{kinematric: } \epsilon_{ij} = (u_{i,j} + u_{j, i})/2\nonumber\]

\[\text{constitutive: } \epsilon_{ij} = \dfrac{1 + \nu}{E} \sigma_{ij} - \dfrac{\nu}{E} \delta_{ij} \sigma_{kk} + \alpha \delta_{ij} \Delta T\nonumber\]

де\(\alpha\) - коефіцієнт лінійного теплового розширення і\(\Delta T\) - зміна температури.

Вправа\(\PageIndex{2}\)

(a) Випишіть матрицю відповідності\(S\) рівняння 3.4.3 для полікарбонату, використовуючи дані в Модулі властивостей матеріалу.

(b) Використовуйте інверсію матриці для отримання матриці жорсткості\(D\).

(c) Використовуйте множення матриці для отримання напружень, необхідних для індукування деформацій

\[\epsilon = \left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right \} = \left \{ \begin{matrix} 0.02 \\ 0.0 \\ 0.03 \\ 0.01 \\ 0.025 \\ 0.0 \end{matrix} \right \}\nonumber\]

Вправа\(\PageIndex{3}\)

(а) Випишіть матрицю\(S\) відповідності рівняння 3.4.3 для алюмінієвого сплаву, використовуючи дані в Модулі властивостей матеріалу.

(b) Використовуйте інверсію матриці для отримання матриці жорсткості\(D\).

(c) Використовуйте множення матриці для отримання напружень, необхідних для індукування деформацій

\[\epsilon = \left \{ \begin{matrix} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right \} = \left \{ \begin{matrix} 0.01 \\ 0.02 \\ 0.0 \\ 0.0 \\ 0.15 \\ 0.0 \end{matrix} \right \}\nonumber\]

Вправа\(\PageIndex{4}\)

З огляду на тензор напруги

\[\sigma_{ij} = \begin{bmatrix} 1 & 2 & 3 \\ 2 & 4 & 5 \\ 3 & 5 & 7 \end{bmatrix} \ \ \text{(MPa)}\nonumber\]

(а) дисоціювати\(\sigma_{ij}\) на девіаторну та дилатаційну частини\(\sum_{ij}\) і\((1/3) \sigma_{kk} \delta_{ij}\).

(b) За даними\(G = 357\) МПа і\(K = 1.67\) ГПа, отримати тензори девіаторних і дилатаційних деформацій\(e_{ij}\) і\((1/3)\epsilon_{kk} \delta_{ij}\).

(c) Додайте девіаторні та дилатаційні деформаційні компоненти, отримані вище, щоб отримати загальний тензор деформації\(\epsilon_{ij}\).

(d) Обчислити тензор деформації,\(\epsilon_{ij}\) використовуючи альтернативну форму пружного конституційного закону для ізотропних пружних твердих тіл:

\[\epsilon_{ij} = \dfrac{1 + \nu}{E} \sigma_{ij} - \dfrac{\nu}{E} \delta_{ij} \sigma_{kk}\nonumber\]

Порівняйте результат з отриманим в (c).

Вправа\(\PageIndex{5}\)

Надайте аргумент, що будь-яка матриця напружень, що має нульовий слід, може бути перетворена на ту, що має лише нулі по діагоналі; тобто тензор девіаторних напружень\(\sum_{ij}\) представляє стан чистого зсуву.

Вправа\(\PageIndex{6}\)

Випишіть\(x-y\) двовимірну матрицю відповідності\(\bar{S}\) і матрицю жорсткості\(\bar{D}\) (Рівняння 3.4.12) для одного шару графіту/епоксидного композиту з вирівняними по\(x\) осях волокнами.

Вправа\(\PageIndex{7}\)

Випишіть\(x-y\) двовимірну матрицю відповідності\(\bar{S}\) та матрицю жорсткості\(\bar{D}\) (Рівняння 3.4.12) для одного шару графіту/епоксидного композиту з вирівняними волокнами 30\(^{\circ}\) від\(x\) осі.