3.3: Тензорні перетворення

Вступ

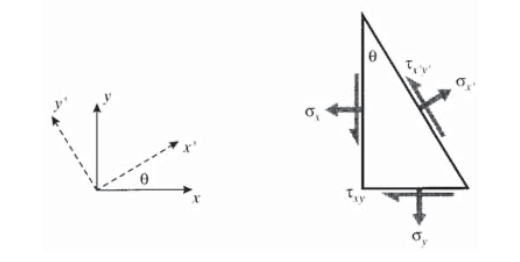
Однією з найпоширеніших проблем механіки матеріалів є перетворення осей. Наприклад, ми можемо знати напруги, що діють на\(xy\) площині, але насправді більше зацікавлені в напруженнях, що діють на площини, орієнтовані на, скажімо, 30\(^{\circ}\) до\(x\) осі, як показано на малюнку 1, можливо, тому, що це близько упаковані атомні площини, на яких ковзання схильне відбуватися, або кут при якому два шматки пиломатеріалу склеюються між собою в «шарф» стик. Ми шукаємо засіб перетворення напружень на ці нові\(x'y'\) площини.

Малюнок 1: Обертання осей у двох вимірах.

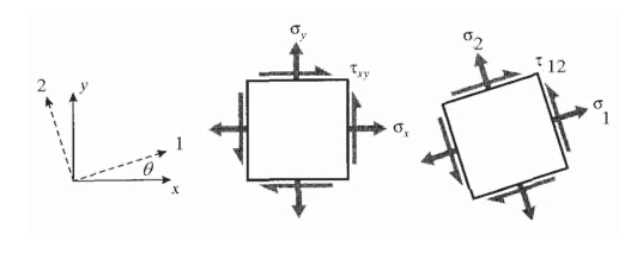
Ці перетворення є життєво важливими для аналізу напружень і деформацій, як тому, що вони необхідні для обчислення критичних значень цих сутностей, так і тому, що тензорний характер напружень і деформації найбільш чітко видно в їх трансформаційних властивостях. Інші сутності, такі як момент інерції та кривизни, також трансформуються таким чином, як напруга та деформація. Все це тензори другого рангу, важлива концепція, яка буде викладена пізніше в цьому модулі.

Прямий підхід

Правила перетворень напруги можуть бути розроблені безпосередньо з міркувань статичної рівноваги. Для ілюстрації розглянемо випадок одновісного натягу, показаний на малюнку 2, в якому всі напруги,\(\sigma_y\) відмінні від нулю. Потім будується діаграма вільного тіла, в якій зразок «розрізається» по похилій площині, на якій бажані напруги\(\tau_{x'y'}\),\(\sigma_{y'}\) позначені і. Ключовим тут є зауваження, що площа, на яку діють ці перетворені напруги, відрізняється від площі, нормальної осі y, так що і ділянки, і сили, що діють на них, повинні бути «перетворені». Балансувальні сили в\(y'\) напрямку (напрямок, нормаль до похилої площини):

Малюнок 2: Похила площина в розтягнутому зразку.

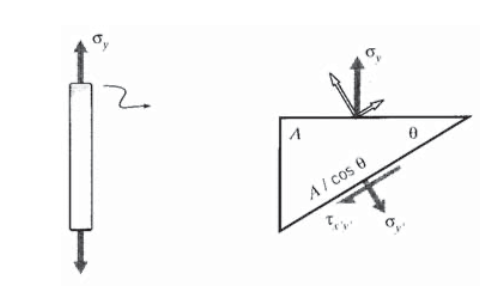
\((\sigma_y A) \cos \theta = \sigma_{y'} \left (\dfrac{A}{\cos \theta} \right )\)

\[\sigma_{y'} = \sigma_y \cos^2 \theta\]

Аналогічно, силовий баланс в дотичному напрямку дає

\[\tau_{x'y'} = \sigma_y \sin \theta \cos \theta\]

Приклад\(\PageIndex{1}\)

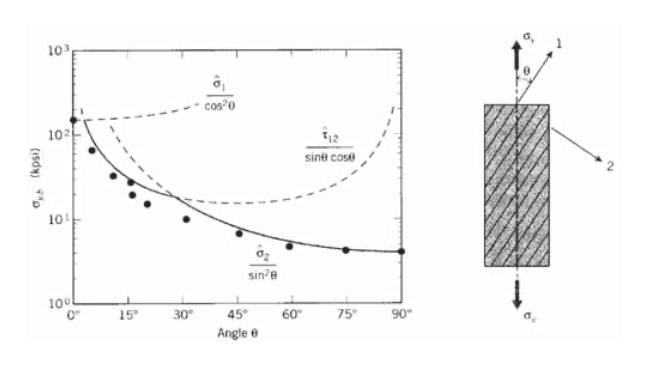
Розглянемо однонаправлено армований композитний шар з міцністю\(\hat{\sigma}_1\) в напрямку волокна,\(\hat{\sigma}_2\) в поперечному напрямку і\(\hat{\tau}_{12}\) в зсуві. Оскільки кут\(\theta\) між напрямком волокна та прикладеною напругою розтягування\(\sigma_y\) збільшується, напруга у напрямку волокна зменшуватиметься відповідно до рівняння 3.3.1. Якби шар вийшов з ладу лише за допомогою руйнування волокна, напруга,\(\sigma_{y, b}\) необхідна для спричинення невдачі, зростала б із зміщенням відповідно до\(\sigma_{y, b} = \hat{\sigma}_1/\cos^2 \theta\).

Однак напруження зсуву, задані рівнянням 3.3.2, збільшуються з\(\theta\), тому напруга σy, необхідна для руйнування зсуву, падає. Міцність\(\sigma_{y,b}\) - це менша з напружень, необхідних для спричинення руйнування напрямку волокна або зсуву, тому міцність стає обмеженою зсувом лише після декількох ступенів перекосу. Фактично,\(^{\circ}\) 15-осьовий зразок на розтяг був запропонований як засіб вимірювання міцності на зсув всередині ламінару. Коли кут орієнтації наближається до 90\(^{\circ}\), руйнування переважає поперечна міцність. Експериментальні дані, показані на малюнку 3, призначені для скляно-епоксидних композитів (R.M. Jones, Механіка композитних матеріалів, McGraw-Hill, 1975.), які показують хорошу, але не точну згоду з цими простими виразами.

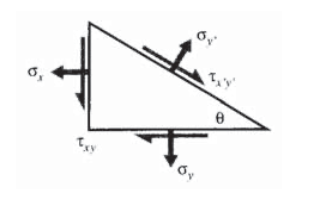
Аналогічний підхід, але узагальнений для включення напружень\(\sigma_x\) і\(\tau_{xy}\) на початкових\(xy\) площинях, як показано на малюнку 4 (див. Вправа\(\PageIndex{2}\)) дає:

\[\begin{array} {rcl} {\sigma_{x'}} & = & {\sigma_x \cos^2 \theta + \sigma_y \sin^2 \theta + 2 \tau_{xy} \sin \theta \cos \theta} \\ {\sigma_{y'}} & = & {\sigma_x \sin^2 \theta + \sigma_y \cos^2 \theta - 2 \tau_{xy} \sin \theta \cos \theta} \\ {\tau_{x'y'}} & = & {(\sigma_y - \sigma_x) \sin \theta \cos \theta + \tau_{xy} (\cos^2 \theta - \sin^2 \theta)} \end{array}\]

Ці відносини можуть бути записані в псевдовекторно-матричному вигляді як

\[\left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\tau_{x'y'}} \end{array} \right \} = \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\tau_{xy}} \end{array} \right \}\]

Малюнок 3: Напруження, прикладене під кутом до волокон в одновимірному шарі.

Малюнок 4: Напруження на похилій площині.

де\(c = \cos \theta\) і\(s = \sin \theta\). Це може бути скорочено як

\[\sigma'=A \sigma\]

де\(A\) матриця перетворення в дужках вище. Цей вираз буде дійсним для тривимірних, а також двовимірних напружених станів, хоча конкретна форма,\(A\) наведена в рівнянні 3.3.4, дійсна лише у двох вимірах (плоска напруга) та для декартових координат.

Використовуючи математичні або геометричні аргументи (див. Вправа\(\PageIndex{3}\) і вправи\(\PageIndex{4}\)), можна показати, що компоненти нескінченно малої деформації трансформуються майже однаковими співвідношеннями:

\[\left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\dfrac{1}{2} \gamma_{x'y'}} \end{array} \right \} = A \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\dfrac{1}{2} \gamma_{xy}} \end{array} \right \}\]

Коефіцієнт 1/2 на складових зсуву виникає з класичного визначення деформації зсуву, яка вдвічі перевищує тензоріальну деформацію зсуву. Це вносить деяку незручність у відносини трансформації, деякі з яких можна зменшити, визначивши матрицю Рейтера як

\[[R] = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 2 \end{bmatrix} \ \ or \ \ [R]^{-1} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & \tfrac{1}{2} \end{bmatrix}\]

Тепер ми можемо написати:

\[\left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\gamma_{x'y'}} \end{array} \right \} = R \left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\dfrac{1}{2} \gamma_{x'y'}} \end{array} \right \} = RA \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\dfrac{1}{2} \gamma_{xy}} \end{array} \right \} = RAR^{-1} \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\gamma_{xy}} \end{array} \right \} \nonumber\]

Або

\[\epsilon' = RAR^{-1} \epsilon\]

Як можна перевірити шляхом розширення цього співвідношення, рівняння перетворення деформації також можна отримати з рівнянь перетворення напружень (наприклад, Рівняння 3.3.3) шляхом заміни на\(\epsilon\) і\(\sigma\)\(\tau\) з\(\gamma /2\):

\[\begin{array} {rcl} {\epsilon_{x'}} & = & {\epsilon_x \cos^2 \theta + \epsilon_y \sin^2 \theta + \gamma_{xy} \sin \theta \cos \theta} \\ {\epsilon_{y'} & = & {\epsilon_x \sin^2 \theta + \epsilon_y \cos^2 \theta - \gamma_{xy} \sin \theta \cos \theta} \\ {\gamma_{x'y'}} & = & {2 (\epsilon_y - \epsilon_x) \sin \theta \cos \theta + \gamma_{xy} (\cos^2 \theta - \sin^2 \theta)} \end{array}\]

Приклад\(\PageIndex{2}\)

Розглянемо двовісний деформований стан

\[\epsilon = \left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\gamma_{x'y'}} \end{array} \right \} = \left \{\begin{array} {c} {0.01} \\ {-0.01} \\ {0} \end{array} \right \} \nonumber\]

Стан деформації, що\(\epsilon'\) відноситься до осей, що обертаються\(\theta = 45^{\circ}\) від\(x-y\) осей, можна обчислити шляхом множення матриці як:

\[A = \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} = \begin{bmatrix} 0.5 & 0.5 & 1.0 \\ 0.5 & 0.5 & -1.0 \\ -0.5 & 0.5 & 0.0 \end{bmatrix} \nonumber\]

Тоді

\[\epsilon' = RAR^{-1} \epsilon \nonumber\]

\[\begin{bmatrix} 1.0 & 1.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 2.0 \end{bmatrix} \begin{bmatrix} 0.5 & 0.5 & 1.0 \\ 0.5 & 0.5 & -1.0 \\ -0.5 & 0.5 & 0.0 \end{bmatrix} \begin{bmatrix} 1.0 & 0.0 & 0.0 \\ 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.5 \end{bmatrix} = \left \{\begin{array} {c} {0.00} \\ {0.00} \\ {-0.02} \end{array} \right \}\nonumber\]

Очевидно, що метод множення матриць виснажливий, якщо не доступне програмне забезпечення для обробки матриць, і в цьому випадку це стає дуже зручним.

Коло Мора

Щоденний досвід таких звичних явищ, як штовхання об'єктів під кутом, дає всім нам певне інтуїтивне відчуття того, як працюють векторні перетворення. Тензорні перетворення другого рангу спочатку здаються більш абстрактними, і пристрій, який допомагає візуалізувати їх, має велику цінність. Як це трапляється, рівняння перетворення мають відому (серед інженерів) графічну інтерпретацію, відому як коло Мора (Представлено в 1900 році німецьким інженером Отто Мором (1835—1918).). Процедура Мора виправдана математично за допомогою тригонометричних подвійних кутових відносин, щоб показати, що Eqns. 3.3.3 мають кругове представлення (див. Вправа\(\PageIndex{5}\)), але це, ймовірно, найкраще можна дізнатися, просто запам'ятовуючи наступний рецепт (Інтерактивна веб-демонстрація кола Мора будівництво доступно за адресою < http://web.mit.edu/course/3/3.11/www/java/mohr.html >.).

1. Намалюйте квадрат напружень, зазначивши значення на гранях x та y; на малюнку 5 (а) показано гіпотетичний випадок для ілюстрації. Тільки для кола Мора розглядайте напругу зсуву, що діє в сенсі обертання за годинниковою стрілкою, як позитивне, а проти годинникової стрілки - як негативне. Потім напруги зсуву на\(y\) гранях\(x\) і повинні мати протилежні ознаки. Нормальні напруги позитивні в розтягуванні і негативні при стисненні, як зазвичай.

Малюнок 5: Квадрат напруги (a) та коло Мора (b) для\(\sigma_x = +5, \sigma_y = -3, \tau_{xy} = +4\). (c) Напружений стан на похилій площині.

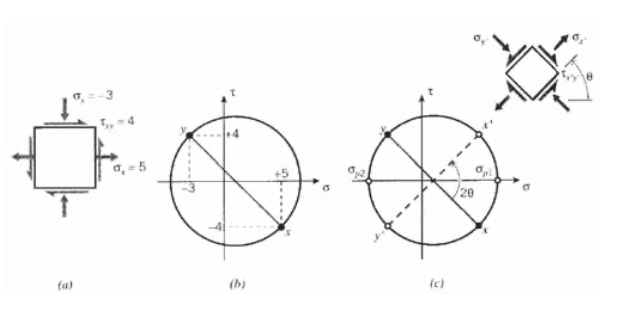
2. Побудуйте графік з\(\tau\) ординатою (\(y\)віссю) та\(\sigma\) абсцисою, і побудуйте напруження на\(x\) та\(y\) гранях квадрата напружень як дві точки на цьому графіку. Оскільки напруження зсуву на цих двох гранях є негативними одна від одної, одна з цих точок буде вище π-осі точно, наскільки інша знаходиться нижче. Корисно позначити ці два пункти як\(x\) і\(y\).

3. З'єднайте ці дві точки прямою лінією. Він перетне\(\sigma\) вісь у середній точці лінії. Ця точка буде в\((\sigma_x + \sigma_y)/2\), який на нашій ілюстрації є [5 + (−3)] /2 = 1.

4. Помістіть точку циркуля в серединній точці лінії, а олівець встановіть в кінці лінії. Намалюйте коло з лінією в якості діаметра. Заповнений коло для нашого ілюстративного напруженого стану показаний на малюнку 5 (б).

5. Для визначення напружень на квадраті напружень, який був повернутий на кут\(\theta\) щодо вихідного квадрата, поверніть діаметральну лінію в тому ж напрямку через удвічі цей кут; т\(2\theta\). Нові кінцеві точки лінії тепер можуть бути\(x'\) позначені і\(y'\), і їх\(\sigma - \tau\) значення є напруженнями на повернутих\(x'-y'\) осях, як показано на малюнку 5 (c).

У колі Мора немає нічого таємничого чи магічного; це просто пристрій, який допомагає візуалізувати, як змінюються напруження та інші тензори другого рангу при обертанні осей.

Дивлячись на коло Мора на малюнку 5 (c), зрозуміло, що є щось особливе у обертанні осі, що призводить до того, що діаметральна лінія стає або горизонтальною, або вертикальною. У першому випадку нормальні напруги припускають максимальні значення, а напруги зсуву дорівнюють нулю. Ці нормальні напруги відомі як основні напруження,\(\sigma_{p1}\) а площини\(\sigma_{p2}\), на яких вони діють, є основними площинами. Якщо матеріал схильний до руйнування внаслідок розтріскування при розтягуванні, він буде робити це шляхом розтріскування вздовж основних площин, коли значення\(\sigma_{p1}\) перевищує міцність на розрив.

Приклад\(\PageIndex{3}\)

Повчально використовувати конструкцію кола Мора, щоб передбачити, як шматок крейди дошки зламається при крученні, а потім перевірити це на практиці. Торсіон створює стан чистого зсуву, як показано на малюнку 6, що призводить до появи головних площин на\(\pm 45^{\circ}\) довгій осі крейди. Тріщина буде здаватися поперечною до основного напруги розтягування, створюючи спіралеподібну поверхню руйнування. (У міру просування тріщини в крейду стан чистого зсуву замінюється більш складним розподілом напружень, тому остання частина поверхні руйнування відхиляється від цього ідеального шляху до одного, що йде уздовж осьового напрямку.) Це той самий тип перелому, який траплявся занадто часто в стегнових кістках лижників, до появи сучасних захисних кріплень.

Малюнок 6: Коло Мора для простого кручення.

Малюнок 7: Основні напруги на колі Мора.

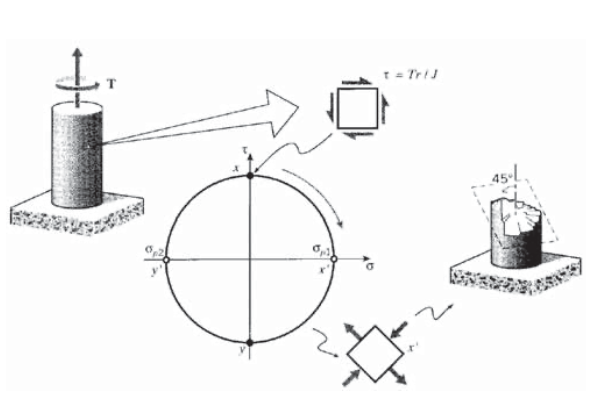
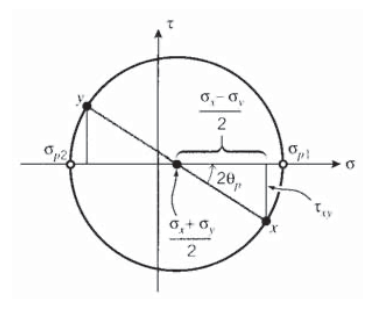
Прямою піфагорійською конструкцією, як показано на малюнку 7, коло Мора показує, що кут від\(x-y\) осей до головних площин дорівнює

\[\tan 2 \theta_p = \dfrac{\tau_{xy}}{(\sigma_x - \sigma_y)/2}\]

і величини основних напружень є

\[\sigma_{p1,p1} = \dfrac{\sigma_x + \sigma_y}{2} \pm \sqrt{(\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2}\]

де перший член вище\(\sigma\) - координата центру кола, а другий - його радіус.

Коли діаметральна лінія кола Мора вертикальна, напруги зсуву стають максимальними, рівними за величиною радіусу кола:

\[\tau_{\max} = \sqrt{(\dfrac{\sigma_x - \sigma_y}{2})^2 + \tau_{xy}^2} = \dfrac{\sigma_{p1} - \sigma_{p2}}{2}\]

Точки максимального зсуву знаходяться на\(^{\circ}\) відстані 90 від основних точок напруги на колі Мора, тому на фактичному зразку площини максимального зсуву знаходяться на 45\(^{\circ}\) від головних площин. Молекулярне ковзання, пов'язане з виходом, приводиться в дію зсувом, і зазвичай відбувається на площинях максимального зсуву. Розтягнутий зразок має головні площини вздовж та поперечно до напрямку завантаження, тому ковзання зсуву буде відбуватися на площині\(\pm\) 45\(^{\circ}\) від напрямку навантаження. Ці площини ковзання часто можна спостерігати як «смуги зсуву» на зразку.

Зверніть увагу, що нормальні напруги можуть з'являтися на площинях максимального зсуву, тому ситуація не зовсім зворотна головних площин, на яких зсувні напруги зникають, тоді як нормальні напруги максимальні. Якщо нормальні напруження зникають на площинях максимального зсуву, стан напруги вважається одним з «чистого зсуву», наприклад, індукується простим крученням. Отже, стан чистого зсуву є тим, для якого обертання осей існує таким чином, що нормальні напруги зникають, що можливо лише в тому випадку, якщо центр кола Мора знаходиться біля початку, тобто\((\sigma_x + \sigma_y)/2 = 0\). Більш загально, стан чистого зсуву - це той, в якому слід матриці напружень (і деформації) зникає.

Приклад\(\PageIndex{4}\)

Малюнок 8: Напруження та напруження кіл Мора для простого зсуву.

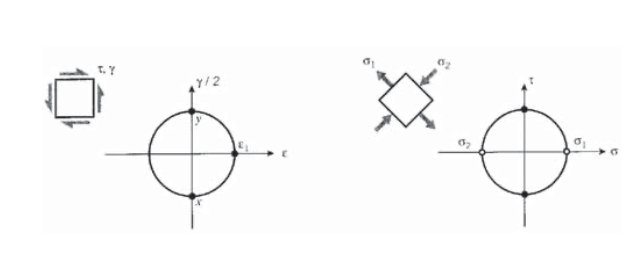
Кола Мора можуть бути намальовані для деформацій, а також напружень, з деформацією зсуву, нанесеною на ординату, і нормальною деформацією на абсцисі. Однак ордината повинна бути\(\gamma/2\) скоріше не просто\(\gamma\), через те, як визначаються класичні нескінченно малі штами. Розглянемо стан чистого зсуву з деформацією\(\gamma\) і напругою,\(\tau\) як показано на малюнку 8, наприклад, може бути отримано шляхом розміщення кругового вала в кручення. Коло Мора для деформації швидко показує основну деформацію, на площині 45\(^{\circ}\) геть, задається\(\epsilon_1 = \gamma/2\). Закон Гука для зсуву дає\(\tau = G \gamma\), так\(\epsilon_1 = \tau /2G\). Основна деформація також пов'язана з основними напруженнями

\[\epsilon_1 = \dfrac{1}{E} (\sigma_2 - \nu \sigma_2)\nonumber\]

Коло Мора для стресу дає\(\sigma_1 = -\sigma_2 = \tau\), так що це можна записати

\[\dfrac{\tau}{2G} = \dfrac{1}{E} [\tau - \nu (-\tau)]\nonumber\]

Скасовуючи\(\tau\) та переставляючи, ми маємо відношення між пружними константами, заявленими раніше без доказів:

\[G = \dfrac{E}{2(1 + \nu)} \nonumber\]

Загальний підхід

Малюнок 9: Трансформація векторів.

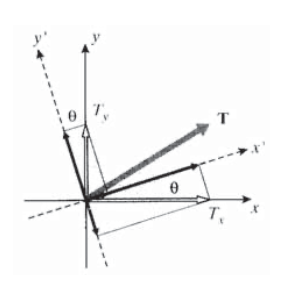
Інший підхід до рівнянь перетворення напружень, здатних легко розширюватися до трьох вимірів, починається зі знайомих відносин, за допомогою яких вектори трансформуються в двох вимірах (див. Рис.

\[T_{x'} = T_x \cos \theta + T_y \sin \theta \nonumber\]

\[T_{y'} = -T_x \sin \theta + T_y \cos \theta \nonumber\]

У матричній формі, тобто

\[\left \{ \begin{array} {c} {T_{x'}} \\ {T_{y'}} \end{array} \right \} = \begin{bmatrix} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{bmatrix} \left \{ \begin{array} {c} {T_{x}} \\ {T_{y}} \end{array} \right \} \nonumber\]

або

\[T' = aT\]

де a - інша матриця перетворення, яка служить для перетворення векторних компонентів у вихідній системі координат до тих, що знаходяться в грунтованій системі. У терміні індексації це також можна було б позначати\(a_{ij}\), так що

\[T_i' = a_{ij} T_j\nonumber\]

Окремими елементами aij є косинуси кутів між\(i^{th}\) загрунтованої віссю і\(j^{th}\) незагрунтованої віссю.

Це може бути показано шляхом безпосереднього вивчення, що матриця має корисну властивість, що її зворотна дорівнює її транспонуванню; тобто,\(a^{-1} = a^T\). Ми можемо помножити Рівняння 3.3. 13 на\(a^T\), щоб дати

\[a^T T' = (a^T a) T = T\]

тому трансформація може перейти від грунтованого до негрунтованого, або зворотного.

Ці відносини можуть бути розширені для отримання виразу для перетворення напружень (або деформацій, або моментів інерції, або інших подібних величин). Нагадаємо відношення Коші в матричній формі:

\[[\sigma] \hat{n} = T\nonumber\]

Використовуючи Equation 3.3.14 для перетворення\(T\) векторів\(\hat{n}\) і в їх загрунтовані аналоги, ми маємо

\[[\sigma] a^T \hat{n}' = a^T T'\nonumber\]

Множення через a:

\ (а [\ сигма] A^t)\ hat {n} '= (AA^t) T' = T'\ nonumber\]

Це просто відношення Коші знову, але в загрунтованій координатній рамці. Тому кількість у дужках повинна бути\([\sigma']\):

\[[\sigma'] = a[\sigma] a^T\]

Тому перетворення напружень і може бути здійснено шляхом до- і постмноження на одну і ту ж матрицю перетворення, застосовну до векторного перетворення. Це також можна виписати за допомогою індексних позначень, що дає ще одну ілюстрацію відмінностей трансформації між скалярами (тензорами нульового рангу), векторами (тензори першого рангу) та тензорами другого рангу:

\[\begin{array} {rcl} {\text{rank 0:}} & \ \ \ & {b' = b} \\ {\text{rank 1:}} & \ \ \ & {T_i' = a_{ij} T_j} \\ {\text{rank 2:}} & \ \ \ & {\sigma_{ij}' = a_{ij} a_{kl} \sigma_{kl}} \end{array}\]

У практичній роботі не завжди просто записати дев'ять елементів матриці, необхідних в Рівнянні 3.3.15. Квадрати складових\(\hat{n}\) для будь-якої заданої площини повинні сумуватися до одиниці, а для того, щоб три площини перетвореного куба напружень були взаємно перпендикулярними, крапковий добуток між будь-якими двома нормалями площини повинен зникнути. Так що не просто будь-які дев'ять чисел матимуть сенс. Отримання a значно полегшується за допомогою «кутів Ейлера» для опису перетворень осей у трьох вимірах.

Малюнок 10: Трансформація з точки зору кутів Ейлера.

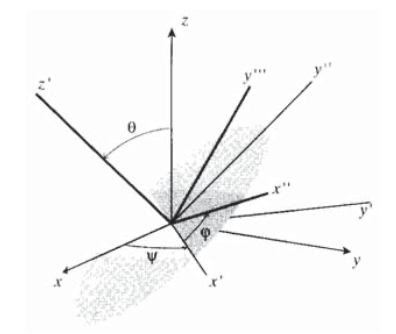
Як показано на малюнку 10, остаточні перетворені осі візуалізуються як досягаються в три кроки: по-перше, поверніть початкові\(x-y-z\) осі на кут\(\psi\) (psi) навколо\(z\) осі -щоб отримати новий кадр, який ми можемо назвати\(x'-y'-z\). Далі поверніть цей новий кадр на кут\(\theta\) навколо\(x'\) осі, щоб отримати інший кадр, який ми можемо назвати\(x'-y''-z'\). Нарешті, поверніть цей кадр на кут\(\phi\) (phi) навколо\(z'\) осі, щоб отримати остаточний кадр\(x''-y'''-z'\). Ці три перетворення відповідають матриці перетворення.

\[a = \begin{bmatrix} \cos \psi & \sin \psi & 0 \\ -\sin \psi & \cos \psi & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \theta & \sin \theta \\ 0 & -\sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \\ 0 & 0 & 1 \end{bmatrix} \nonumber\]

Це множення, безумовно, буде болем, якщо зробити це вручну, але є природним для обчислювального підходу.

Приклад\(\PageIndex{5}\)

Вихідні дані нижче показують комп'ютерну оцінку тривимірного перетворення напруги, в даному випадку за допомогою символічного математичного програмного забезпечення MapleTM.

# read linear algebra library
> with(linalg):
# Define Euler-angle transformation matrices:
> a1:=array(1..3,1..3,[[cos(psi),sin(psi),0],[-sin(psi),cos(psi),0],[0,0 > ,1]]);
                      [cos(psi)     sin(psi)         0] 
                a1 := [-sin(psi)    cos(psi)         0] 
                      [   0              0           1]
> a2:=array(1..3,1..3,[[1,0,0],[0,cos(theta),sin(theta)],[0,-sin(theta), 
> cos(theta)]]);
                      [1       0             0.   ] 
                a2 := [0   cos(theta)   sin(theta)] 
                      [0.  -sin(theta)  cos(theta)]
> a3:=array(1..3,1..3,[[cos(phi),sin(phi),0],[-sin(phi),cos(phi),0],[0,0 > ,1]]);
                      [cos(phi)     sin(phi)     0] 
                a3 := [-sin(phi)    cos(phi)     0] 
                      [    0             0       1] 
# Overall transformation matrix (multiply individual Euler matrices):
> a:=a1&*a2&*a3;
                       a := (a1 &* a2) &* a3
# Set precision and read in Euler angles (converted to radians); here
# we are rotating 30 degrees around the z axis only. 
> Digits:=4;psi:=0;theta:=30*(Pi/180);phi:=0;
                             Digits := 4
                               psi := 0
                          theta := 1/6 Pi 
                               phi := 0
# Display transformation matrix for these angles: "evalf" evaluates the 
# matrix element, and "map" applies the evaluation to each element of
# the matrix.
> aa:=map(evalf,evalm(a));
                        [1.      0.      0.  ]
                  aa := [0.    .8660    .5000]
                        [0.   -.5000    .8660]
# Define the stress matrix in the unprimed frame:
> sigma:=array(1..3,1..3,[[1,2,3],[2,4,5],[3,5,6]]);
                                 [1    2    3] 
                        sigma := [2    4    5] 
                                 [3    5    6]
# The stress matrix in the primed frame is then given by Equation 15: 
> ’sigma_prime’=map(evalf,evalm(aa&*sigma&*transpose(aa)));
                          [1      3.232     1.598]
            sigma_prime = [3.232  8.830     3.366]
                          [1.598  3.366     1.170]  

Основні напруги і площини в трьох вимірах

Малюнок 11: Вектор тяги, нормаль до головної площини.

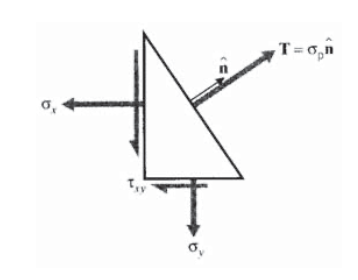
Процедура кола Мора не здатна знайти основні напруги для тривимірних напружених станів, і потрібен більш загальний метод. У трьох вимірах ми шукаємо орієнтації осей таким чином, щоб не виникало напружень зсуву, залишаючи лише нормальні напруги в трьох ортогональних напрямках. Зникнення напружень зсуву на площині означає, що вектор напружень\(T\) є нормальним до площини, проілюстрований у двох вимірах на малюнку 11. Тому вектор тяги можна записати як

\[T= \sigma_p \hat{n}\nonumber\]

де\(\sigma_p\) - проста скалярна величина, величина вектора напружень. Використовуючи це у відношенні Коші:

\[\sigma \hat{n} = T = \sigma_p \hat{n}\nonumber\]

\[(\sigma - \sigma_p I) \hat{n} = 0\]

\(I\)Ось матриця одиниць. Ця система матиме нетривіальне рішення (\(\hat{n} \ne 0\)) тільки в тому випадку, якщо її детермінант дорівнює нулю:

\[|\sigma - \sigma_p I| = \left | \begin{matrix} \sigma_x - \sigma_p & \tau_{xy} & \tau_{xz} \\ \tau_{xy} & \sigma_y - \sigma_p & \tau_{yz} \\ \tau_{xz} & \tau_{yz} & \sigma_z - \sigma_p \end{matrix} \right | = 0\nonumber\]

Розширення детермінанти дає кубічне рівняння полінома в\(\sigma_p\):

\[f(\sigma_p) = \sigma_p^3 - I_1 \sigma_p^3 + I_2 \sigma_p - I_3 = 0\]

Це характерне рівняння для напружень, де коефіцієнти

\[I_1 = \sigma_x + \sigma_y + \sigma_z = \sigma_{kk}\]

\[I_2 = \sigma_x \sigma_y + \sigma_x \sigma_z + \sigma_y \sigma_z - \tau_{xy}^2 - \tau_{yz}^2 - \tau_{xz}^2 = \dfrac{1}{2} (\sigma_{ii} \sigma_{jj} - \sigma_{ij} \sigma_{ij})\]

\[I_3 = \text{det} |\sigma| = \dfrac{1}{3} \sigma_{ij} \sigma_{jk} \sigma_{ki}\]

Ці\(I\) параметри відомі як інваріанти напруженого стану; вони не змінюються з перетворенням координат і можуть бути використані для характеристики загального характеру напружень. Наприклад\(I_1\), який раніше був ідентифікований як слід матриці напружень, буде розглядатися в більш пізньому розділі, щоб бути мірою тенденції напруженого стану індукувати гідростатичне розширення або стиснення. Ми вже відзначали, що напружений стан є одним з чистого зсуву, якщо його слід зникає.

Оскільки характеристичне рівняння є кубічним в\(\sigma_p\), воно буде мати три кореня, і можна показати, що всі три кореня повинні бути реальними. Ці корені є лише основними стресами\(\sigma_{p1}\),\(\sigma_{p2}\) і\(\sigma_{p3}\).

Приклад\(\PageIndex{6}\)

Розглянемо стан простого зсуву з нульовими\(\tau_{xy} = 1\) і всіма іншими напруженнями:

\[|\sigma| = \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\nonumber\]

Інваріанти є

\[I_1 = 0, I_2 = -1, I_3 = 0\nonumber\]

і характеристичне рівняння

\[\sigma_p^3 - \sigma_p = 0\nonumber\]

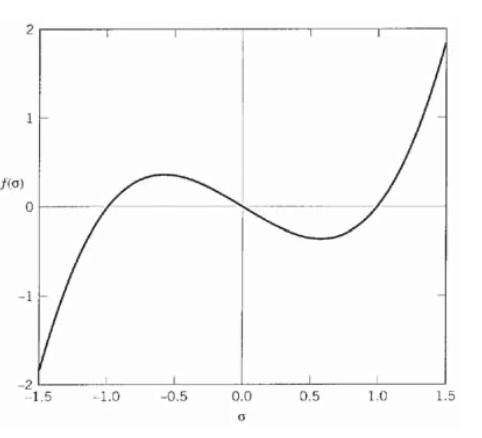
Це рівняння має коріння (-1, 0, 1), відповідні основним напруженням\(\sigma_{p1} = 1, \sigma_{p2} = 0, \sigma_{p3} = -1\), і побудовано на малюнку 12. Це той самий напружений стан, розглянутий у прикладі 4, і коріння характеристичного рівняння узгоджуються з основними значеннями, показаними колом Мора.

Малюнок 12: Характеристичне\(\tau_{xy} = 1\) рівняння для всіх інших напружень нуль.

Вправа\(\PageIndex{1}\)

Розробити вираз для напруги, необхідного для спричинення поперечного руйнування в однонаправленно орієнтованому композиту як функції кута між напрямком навантаження та напрямком волокна, і показати цю функцію на графіку сили проти\(\theta\).

Вправа\(\PageIndex{2}\)

Використовуйте баланс сили вільного тіла для отримання двовимірних декартових рівнянь перетворення напружень як

\[\begin{array} {rcl} {\sigma_{x'}} & = & {\sigma_x \cos^2 \theta + \sigma_y \sin^2 \theta + 2 \tau_{xy} \sin \theta \cos \theta} \\ {\sigma_{y'}} & = & {\sigma_x \sin^2 \theta + \sigma_y \cos^2 \theta - 2 \tau_{xy} \sin \theta \cos \theta} \\ {\tau_{x'y'}} & = & {(\sigma_y - \sigma_x) \sin \theta \cos \theta + \tau_{xy} (\cos^2 \theta - \sin^2 \theta)} \end{array} \nonumber\]

Або

\[\left \{\begin{array} {c} {\sigma_{x'}} \\ {\sigma_{y'}} \\ {\tau_{x'y'}} \end{array} \right \} = \begin{bmatrix} c^2 & s^2 & 2sc \\ s^2 & c^2 & -2sc \\ -sc & sc & c^2 - s^2 \end{bmatrix} \left \{\begin{array} {c} {\sigma_{x}} \\ {\sigma_{y}} \\ {\tau_{xy}} \end{array} \right \}\nonumber\]

де\(c = \cos \theta\) і\(s = \sin \theta\)

Вправа\(\PageIndex{3}\)

Розробити математичні відносини для переміщень і градієнтів уздовж перетворених осей форми

\[u' = u \cos \theta + v \sin \theta \nonumber\]

\[\dfrac{\partial}{\partial x'} = \dfrac{\partial}{\partial x} \cdot \dfrac{\partial x}{\partial x'} + \dfrac{\partial}{\partial y} \cdot \dfrac{\partial y}{\partial x'} = \dfrac{\partial}{\partial x} \cdot \cos \theta + \dfrac{\partial}{\partial y} \cdot \sin \theta \nonumber\]

з аналогічними виразами для\(v'\) і\(\partial /\partial y'\). Використовуйте їх для отримання рівнянь перетворення деформації (Рівняння 3.3.6).

Вправа\(\PageIndex{4}\)

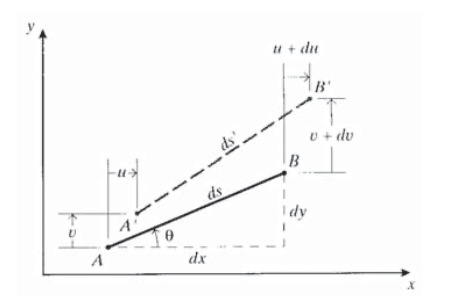
Розглянемо відрізок\(AB\) прямої довжини\(ds^2 = dx^2 + dy^2\), орієнтований під кутом\(\theta\) від декартових\(x - y\) осей, як показано на малюнку. Нехай диференціальне зміщення кінця\(B\) відносно кінця\(A\) буде

\[du = \dfrac{\partial u}{\partial x} dx + \dfrac{\partial u}{\partial y} dy\nonumber\]

\[dv = \dfrac{\partial v}{\partial x} dx + \dfrac{\partial v}{\partial y} dy\nonumber\]

Використовуйте цю геометрію для отримання рівнянь перетворення деформації (Equation 3.3.6), де\(x'\) вісь знаходиться вздовж лінії\(AB\).

Вправа\(\PageIndex{5}\)

Використовуйте двокутні тригонометричні відносини, щоб показати, що двовимірні декартові рівняння перетворення напружень можуть бути записані у вигляді

\[\begin{array} {rcr} {\sigma_{x'}} & = & {\tfrac{\sigma_x + \sigma_y}{2} + \tfrac{\sigma_x - \sigma_y}{2} \cos 2 \theta + \tau_{xy} \sin 2 \theta} \\ {\tau_{x'y'}} & = & {-\tfrac{\sigma_x - \sigma_y}{2} \sin 2 \theta + \tau_{xy} \cos 2\theta} \\ {\sigma_{y'}} & = & {\tfrac{\sigma_x + \sigma_y}{2} + \tfrac{\sigma_x - \sigma_y}{2} \cos 2 \theta - \tau_{xy} \sin 2 \theta} \end{array} \nonumber\]

Використовуйте ці відносини для обґрунтування побудови кола Мора.

Вправа\(\PageIndex{6}\)

Використовуйте множення матриці (Eqns. 3.3.5 або 3.3.8) для перетворення наступних напружених і деформаційних станів на осі, повернуті\(\theta = 30^{\circ}\) від початкових\(x-y\) осей.

(а)

\[\sigma = \left \{ \begin{array} {c} {1.0} \\ {-2.0} \\ {3.0} \end{array} \right \}\nonumber\]

(б)

\[\epsilon = \left \{ \begin{array} {c} {0.01} \\ {-0.02} \\ {0.03} \end{array} \right \}\nonumber\]

Вправа\(\PageIndex{7}\)

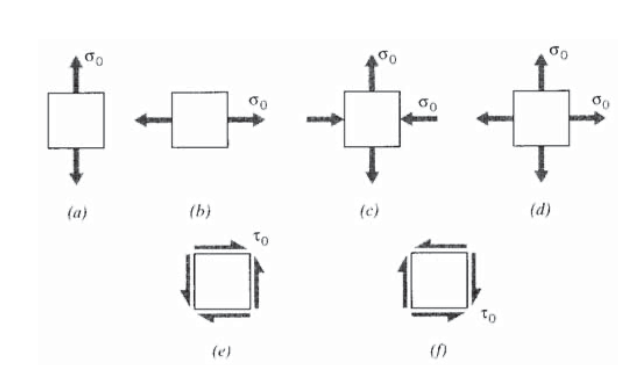
Намалюйте кола Мора для кожного з напружених станів, показаних на малюнку нижче.

Вправа\(\PageIndex{8}\)

Побудувати коло розв'язків Мора для перетворень вправи\(\PageIndex{6}\).

Вправа\(\PageIndex{9}\)

Намалюйте кола Мора і визначте величини головних напружень для наступних напружених станів. Позначте основний напружений стан на відповідним чином повернутому квадраті напруги.

(а)\(\sigma_x = 30\) МПа,\(\sigma_y = -10\) МПа,\(\tau_{xy} = 25\) МПа.

(б)\(\sigma_x = -30\) МПа,\(\sigma_y = -90\) МПа,\(\tau_{xy} = -40\) МПа.

(c)\(\sigma_x = -10\) МПа,\(\sigma_y = 20\) МПа,\(\tau_{xy} = -15\) МПа.

Вправа\(\PageIndex{10}\)

Показати, що значення головних напружень, заданих колом Мора, узгоджуються з тими, що отримані математично шляхом встановлення на нуль похідних напруг щодо кута перетворення.

Вправа\(\PageIndex{11}\)

Для 3-мірного напруженого стану\(\sigma_x = 25, \sigma_y = -15, \sigma_z = -30, \tau_{yz} = 20, \tau_{xz} = 10, \tau_{xy} = 30\) (все в МПа):

(а) Визначити напружений стан для кутів Ейлера\(\psi = 20^{\circ}\),\(\theta = 30^{\circ}\),\(\phi = 25^{\circ}\).

(б) Побудуйте характеристичне рівняння.

(в) Визначити основні напруги.