3.1: Кінематика

Вступ

Кінематичні або деформаційні рівняння зміщення описують, як деформації - розтягнення та спотворення - всередині навантаженого тіла відносяться до переміщень тіла. Компоненти зміщення в\(x, y\), і\(z\) напрямки позначаються вектором\(u \equiv u_i \equiv (u,v,w)\), і є функціями положення всередині тіла:\(u = u(x, y, z)\). Якщо всі точки всередині матеріалу відчувають однакове зміщення (u = постійна), конструкція рухається як тверде тіло, але не розтягується і не деформується всередині. Щоб розтягування відбулося, точки всередині тіла повинні відчувати різні зміщення.

Нескінченно малий штам

Малюнок 1: Інкрементна деформація.

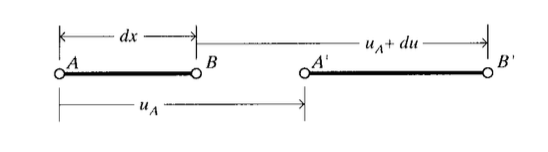
Розглянемо дві точки\(A\) і\(B\) розділені спочатку невеликою\(dx\) відстанню, як показано на малюнку 1, і відчуваємо рух у\(x\) напрямку. Якщо зміщення в точці\(A\) є\(u_A\), зміщення в\(B\) може бути виражено розширенням серії Тейлора\(u(x)\) навколо точки\(x = A\):

\(u_B = u_A + du = u_A + \dfrac{\partial u}{\partial x} dx\)

де тут розширення було скорочено після другого терміну. Диференціальний рух\(\delta\) між двома точками

У нашій концепції розтягування як диференціального зміщення на одиницю довжини, то\(x\) компонент деформації

\[\epsilon_x = \dfrac{\delta}{dx} = \dfrac{\partial u}{\partial x}\]

Звідси деформація - це градієнт зсуву. Застосовуючи подібні міркування до диференціального руху в\(y\) напрямку,\(y\) -складовою деформації є градієнт вертикального\(v\) зміщення щодо\(y\):

\[\epsilon_y = \dfrac{\partial v}{\partial y}\]

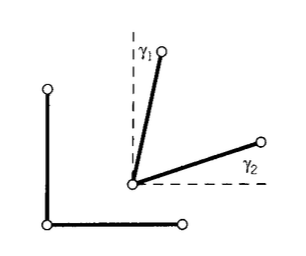
Малюнок 2: Спотворення зсуву.

Спотворення матеріалу, яке можна охарактеризувати як зміна спочатку прямих кутів, - це сума нахилів, наданих вертикальним і горизонтальним лініям. Як показано на малюнку 2, нахил спочатку вертикальної лінії - це відносне горизонтальне зміщення двох сусідніх точок уздовж лінії:

Зміна кута - це

\(\gamma_1 \approx \tan \gamma_1 = \dfrac{\delta}{dy} = \dfrac{\partial u}{\partial y}\)

Аналогічно (див. Рис. 3) нахил\(\gamma_2\) початкової горизонтальної лінії є\(v\) градієнтом щодо\(x\). Потім деформація зсуву в\(xy\) площині

\[\gamma_{xy} = \gamma_1 + \gamma_2 = \dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\partial y}\]

Це позначення, яке використовується\(\epsilon\) для нормальної деформації та\(\gamma\) для деформації зсуву, іноді називають «класичним» описом штаму.

Формулювання матриці

«Індикальне позначення», описане в Модулі матричних та індексних позначень, забезпечує стислий метод запису всіх складових тривимірних станів деформації:

\[\epsilon_{ij} = \dfrac{1}{2} \left ( \dfrac{\partial u_i}{\partial x_j} + \dfrac{\partial u_j}{\partial x_i} \right ) = \dfrac{1}{2} (u_{i,j} + u_{j, i})\]

Малюнок 3: Штам зсуву.

де кома позначає диференціювання щодо наступної просторової змінної. Це двоіндексне позначення індексу призводить природно до матричного розташування деформаційних компонентів, в якому\(i-j\) компонент деформації стає елементом матриці в\(i^{th}\) рядку і\(j^{th}\) стовпці:

\[\epsilon_{ij} = \begin{bmatrix} \tfrac{\partial u}{\partial x} & \tfrac{1}{2} (\tfrac{\partial u}{\partial y} + \tfrac{\partial v}{\partial x}) & \tfrac{1}{2} (\tfrac{\partial u}{\partial z}+ \tfrac{\partial w}{\partial x}) \\ \tfrac{1}{2} (\tfrac{\partial u}{\partial y} + \tfrac{\partial v}{\partial x}) & \tfrac{\partial v}{\partial y} & \tfrac{1}{2} (\tfrac{\partial v}{\partial z} + \tfrac{\partial w}{\partial y}) \\ \tfrac{1}{2} (\tfrac{\partial w}{\partial x} + \tfrac{\partial u}{\partial z}) & \tfrac{1}{2} (\tfrac{\partial v}{\partial z} + \tfrac{\partial w}{\partial y}) & \tfrac{\partial w}{\partial z} \end{bmatrix}\]

Зверніть увагу, що матриця деформацій симетрична, т\(\epsilon_{ij} = \epsilon_{ji}\). Ця симетрія означає, що існує шість, а не дев'ять незалежних штамів, як можна було очікувати в матриці\(\times\) 3 3. Також зверніть увагу, що індикальний опис штаму дає той же результат для нормальних компонентів, що і в класичному описі:\(\epsilon_{11} = \epsilon_x\). Однак індикальними складовими деформації зсуву є половина їх класичних побратимів:\(\epsilon_{12} = \gamma_{xy}/2\).

У ще одній корисній нотаційній схемі класичні рівняння деформації-зміщення можуть бути виписані у вертикальний список, аналогічний вектору:

\(\left \{ \begin{array} {c} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{array} \right \} = \left \{ \begin{array} {c} {\partial u/\partial x} \\ {\partial v/\partial y} \\ {\partial w/\partial z} \\ {\partial v/\partial z + \partial w/\partial y} \\ {\partial u/\partial z + \partial w/\partial x} \\ {\partial u/\partial y + \partial v/\partial x} \end{array} \right \}\)

Це векторне розташування компонентів деформації тільки для зручності, і іноді його називають псевдовектором. Деформація насправді є тензором другого рангу, як напруга або момент інерції, і має математичні властивості, дуже різні, ніж у векторів. Порядок елементів у формі псевдовектора є довільним, але зазвичай перераховувати їх, як ми маємо тут, рухаючись вниз по діагоналі матриці деформації рівняння 5 зверху ліворуч вниз праворуч, потім перемістіть вгору третій стовпець і, нарешті, перемістіть один стовпець вліво на першому рядку; це дає замовлення 1,1; 2,2; 3,3; 2,3; 1,3; 1,2.

Дотримуючись правил множення матриці, псевдовектор деформації також може бути записаний через вектор зміщення як

\[\left \{ \begin{array} {c} \epsilon_x \\ \epsilon_y \\ \epsilon_z \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{array} \right \} = \begin{bmatrix} \partial/\partial x & 0 & 0 \\ 0 & \partial/\partial y & 0 \\ 0 & 0 & \partial/\partial z \\ 0 & \partial /\partial z & \partial /\partial y \\ \partial /\partial z & 0 & \partial/\partial x \\ \partial/\partial y & \partial/\partial x & 0 \end{bmatrix} \left \{ \begin{array} {c} u \\ v \\ w \end{array} \right \}\]

Матриця в дужках вище, елементами якої є диференціальні оператори, може бути скорочена так\(L\):

\[L = \begin{bmatrix} \partial/\partial x & 0 & 0 \\ 0 & \partial/\partial y & 0 \\ 0 & 0 & \partial/\partial z \\ 0 & \partial /\partial z & \partial /\partial y \\ \partial /\partial z & 0 & \partial/\partial x \\ \partial/\partial y & \partial/\partial x & 0 \end{bmatrix}\]

Рівняння деформації-зміщення потім можуть бути записані в стислому вигляді «псевдовектор-матриця»:

\[\epsilon = Lu\]

Такі рівняння повинні використовуватися у чітко визначеному контексті, оскільки вони застосовуються лише тоді, коли використовується дещо довільний псевдовекторний перелік компонентів деформації.

Об'ємна деформація

Оскільки нормальна деформація - це лише зміна довжини на одиницю початкової довжини, нова довжина\(L'\) після напруження виявляється як

\[\epsilon = \dfrac{L' - L_0}{L_0} \Rightarrow L' = (1 + \epsilon) L_0\]

Якщо кубічний об'ємний елемент, спочатку розмірності\(abc\), піддається нормальним деформаціям у всіх трьох напрямках, зміна об'єму елемента дорівнює

\[\begin{array} {rcl} {\dfrac{\Delta V}{V}} & = & {\dfrac{a'b'c' - abc}{abc} = \dfrac{a(1 + \epsilon_x) b(1 + \epsilon_y) c(1+\epsilon_z) - abc}{abc}} \\ {} & = & {(1 + \epsilon_x)(1 + \epsilon_y)(1 +\epsilon_z) - 1 \approx \epsilon_x + \epsilon_y + \epsilon_z} \end{array}\]

де продуктами штамів нехтують в порівнянні з окремими значеннями. Тому об'ємна деформація - це сума нормальних деформацій, тобто сума діагональних елементів у деформаційній матриці (це також називається слідом матриці, або\(Tr[\epsilon]\)). У позначеннях індексу це можна записати просто

\(\dfrac{\Delta V}{V} = \epsilon_{kk}\)

Це відомо як об'ємний, або «дилатаційний» компонент деформації.

Приклад\(\PageIndex{1}\)

Щоб проілюструвати, як розраховується об'ємна деформація, розглянемо тонкий лист сталі, що піддається деформаціям в його площині\(\epsilon_x = 3, \epsilon_y = -4\), заданої, і\(\gamma_{xy} = 6\) (все в\(\mu\) в/в). Лист не знаходиться в плоскому деформації, так як він може піддаватися деформації Пуассона в\(z\) напрямку, заданому\(\epsilon_z = -\nu (\epsilon_x + \epsilon_y) = -0.3(3 - 4) = 0.3\). Таким чином, загальний стан деформації може бути записаний як матриця

де дужки на\([\epsilon]\) символі підкреслюють, що використовується матрична, а не псевдовекторна форма деформації. Об'ємна деформація буває:

Інженери часто посилаються на «мікродюйми» деформації; вони дійсно означають мікродюйми на дюйм. У разі об'ємного деформації відповідною (але незручною) одиницею буде мікро-кубічні дюйми на кубічний дюйм.

скінченний штам

У переважній більшості механічних аналізів використовуються нескінченно малі співвідношення деформації-зміщення, задані Eqns. 3.1.1—3.1.3, але вони не описують розтягування точно, коли градієнти зміщення стають великими. Це часто відбувається при розгляді полімерів (особливо еластомерів). Великі деформації також виникають під час операцій деформаційної обробки, таких як штампування сталевих автомобільних панелей кузова. Кінематика великого зміщення або деформації може бути складною і тонкою, але в наступному розділі буде викладено простий опис кінцевого деформації Лагранжа, щоб проілюструвати деякі з задіяних понять.

Розглянемо дві ортогональні лінії\(OB\) і\(O\) А як показано на малюнку 4, спочатку довжини dx і dy, уздовж\(x-y\) осей, де для зручності ставимо\(dx = dy = 1\). Після деформації кінцеві точки цих ліній переміщуються на нові позиції,\(A_1O_1B_1\) як показано на малюнку. Ми опишемо ці нові позиції, використовуючи схему координат вихідних\(x-y\) осей, хоча ми також могли б дозволити новим позиціям визначити новий набір осей. Слідуючи за рухом ліній щодо вихідних позицій, ми використовуємо так звану точку зору Лагранжа. Ми могли б поперемінно використовувати кінцеві позиції як наш орієнтир; це погляд Ейлера, який часто використовується в механіці рідини.

Після напруження відстань\(dx\) стає

\((dx)' = (1 + \dfrac{\partial u}{\partial x} dx\)

Використовуючи наше попереднє «маленьке» мислення,\(x\) напруга -direction буде просто\(\partial u /\partial x\). Але коли штами стають більше, ми також повинні враховувати, що висхідний рух точки\(B_1\) щодо\(O_1\)\(\partial v /\partial x\), тобто також допомагає розтягнути лінію\(OB\). Враховуючи обидва ці ефекти, теорема Піфагора дає нову довжину\(O_1B_1\) як

\(O_1 B_1 = \sqrt{(1 + \dfrac{\partial u}{\partial x})^2 + (\dfrac{\partial v}{\partial x})^2}\)

Тепер ми визначаємо наш штам Лагранжа як

Малюнок 4: Кінцеві зсуви.

\ [4pt] &=\ sqrt {1 + 2\ dfrac {\ частковий u} {\ частковий х} +\ лівий (\ dfrac {\ частковий u} {\ частковий х}\ праворуч) ^2 +\ ліворуч (\ dfrac {\ частковий v} {\ частковий х}\ правий) ^2} - 1\ кінець {вирівня*}\] </p lt-445356 ">

Використовуючи розширення серії\(\sqrt{1 + x} \approx 1 + x/2 + x^2/8 + \cdots\) та нехтування термінами поза першим порядком, це стає

Точно так само ми можемо показати

\[\epsilon_y = \dfrac{\partial v}{\partial y} + \dfrac{1}{2} \left [\left ( \dfrac{\partial v}{\partial y} \right )^2 \left ( \dfrac{\partial u}{\partial y} \right )^2 \right ]\]

\[\gamma_{xy} = \dfrac{\partial u}{\partial y} + \dfrac{\partial v}{\partial x} + \dfrac{\partial u}{\partial y} \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} \dfrac{\partial v}{\partial x}\]

Коли деформації досить малі, щоб квадратичні члени були незначними порівняно з лінійними, вони зводяться до нескінченно малодеформаційних виразів, показаних раніше.

Приклад\(\PageIndex{2}\)

Функція переміщення\(u(x)\) для розтяжного зразка рівномірного перерізу та довжини\(L\), закріпленого на одному кінці та підданого зміщенню\(\delta\) на іншому, є лише лінійним співвідношенням

\(u(x) = \left ( \dfrac{x}{L} \right ) \delta\)

Потім деформація Лагранжа задається рівнянням 3.1.11 як

\(\epsilon_x = \dfrac{\delta}{L} + \dfrac{1}{2} \left ( \dfrac{\delta}{L} \right )^2\)

Перший термін - це знайоме дрібнодеформаційний вираз, при цьому другий нелінійний термін стає все більш важливим, оскільки\(\delta\) стає більшим. Коли\(\delta = L\), тобто звичайний штам 100%, існує 50% різниця між звичайними та лагранжевими мірами деформації.

Компоненти штаму Лагранжа можна узагальнити за допомогою індексних позначень як

\(\epsilon_{ij} = \dfrac{1}{2} (u_{i,j} + u_{j, i} + u_{r, i} u_{r, j})\).

Псевдовекторна форма також зручна зрідка:

\[ \begin{align*} \left \{ \begin{array} {c} {\epsilon_x} \\ {\epsilon_y} \\ {\gamma_{xy}} \end{array} \right \} &= \left \{ \begin{array} {c} {u_{,x}} \\ {v_{,y}} \\ {u_{,y} + v_{,x}} \end{array} \right \} + \dfrac{1}{2} \begin{bmatrix} u_{,x} & v_{,x} & 0 & 0 \\ 0 & 0 & u_{,y} & v_{,y} \\ u_{,y} & v_{,y} & u_{,x} & v_{,x} \end{bmatrix} \left \{ \begin{array} {c} {u_{,x}} \\ {v_{,x}} \\ {u_{,y}} \\ {v_{,y}} \end{array} \right \} \\[4pt] &= \left (\begin{bmatrix} \partial /\partial x & 0 \\ 0 & \partial /\partial y \\ \partial /\partial y & \partial /\partial x \end{bmatrix} + \dfrac{1}{2} \begin{bmatrix} u_{,x} & v_{,x} & 0 & 0 \\ 0 & 0 & u_{,y} & v_{,y} \\ u_{,y} & v_{,y} & u_{,x} & v_{,x} \end{bmatrix} \begin{bmatrix} \partial /\partial x & 0 \\ 0 & \partial /\partial x \\ \partial /\partial y & 0 \\ 0 & \partial /\partial y \end{bmatrix}\right ) \left \{ \begin{array} {c} {u} \\ {v} \end{array} \right \} \end{align*}\]

які можуть бути скорочені

\[\epsilon = [L + A(u)]u\]

Матриця\(A(u)\) містить нелінійний ефект великої деформації і стає незначною, коли деформації малі.

Вправа\(\PageIndex{1}\)

Випишіть скорочене рівняння деформації-зміщення\(\epsilon = Lu\) (Рівняння 3.1.8) для двох вимірів.

Вправа\(\PageIndex{2}\)

Випишіть компоненти тензора деформації Лагранжа в трьох вимірах:

\(\epsilon_{ij} = \dfrac{1}{2} (u_{i,j} + u_{j, i} + u_{r, i} u_{r, j})\)

Вправа\(\PageIndex{3}\)

Показати, що для малих деформацій дробова зміна об'єму є слідом тензора нескінченно малих деформацій:

\(\dfrac{Delta V}{V} \equiv \epsilon_{kk} = \epsilon_x + \epsilon_y + \epsilon_z\)

Вправа\(\PageIndex{4}\)

Коли матеріал нестисливий, покажіть коефіцієнти розширення пов'язані

\(\lambda_x \lambda_y \lambda_z = 1\)

Вправа\(\PageIndex{5}\)

Показати, що кінематичні відносини (деформація-зміщення) для полярних координат можуть бути записані

\(\epsilon_r = \dfrac{\partial u_r}{\partial r}\)

\(\epsilon_{\theta} = \dfrac{1}{r} \dfrac{\partial u_{\theta}}{\partial \theta} +\dfrac{u_r}{r}\)