3.2: Рівновага

Вступ

Кінематичні відносини, описані в Модулі 8, є чисто геометричними і не передбачають міркувань поведінки матеріалу. Співвідношення рівноваги, які будуть обговорюватися в цьому модулі, мають таку ж незалежність від матеріалу. Вони просто закон руху Ньютона, який стверджує, що за відсутності прискорення всі сили, що діють на тіло (або його шматок), повинні балансувати. Це дозволяє нам констатувати, як напруга всередині тіла, але оцінюється трохи нижче поверхні, пов'язана із зовнішньою силою, прикладеною до поверхні. Він також регулює, як стрес змінюється від положення до положення всередині тіла.

стрес Коші

Малюнок 1: Вектор тяги.

У попередніх модулів ми виражали нормальне напруження як силу на одиницю площі, що діє перпендикулярно до вибраної області, а напруга зсуву була силою на одиницю площі, що діє поперечно площі. Щоб узагальнити це поняття, розглянемо ситуацію, зображену на малюнку 1, при якій вектор тяги Т діє на довільну площину всередині або на зовнішній межі тіла, і в довільному напрямку щодо орієнтації площини. Тяга являє собою простий вектор сили, що має величину і напрямок, але її величина виражається через силу на одиницю площі:

$$T = \lim_{\Delta A \to 0} \left (\dfrac{\Delta F}{\Delta A} \right )$$

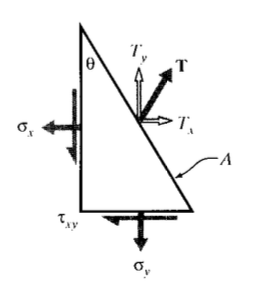
де$\Delta A$ - величина площі, на яку діє ΔF. Коші (барон Августин-Луї Коші (1789 {1857) був плідним французьким інженером і математиком) напруження, які є узагальненням наших попередніх визначень стресу, є сили на одиницю площі, що діють на декартові$x$$y$, і$z$ площинами до збалансувати тягу. У двох вимірах цей баланс можна записати, намалювавши просту діаграму вільного тіла з вектором тяги, що діє на ділянку довільного розміру$A$ (рис. 2), пам'ятаючи про отримання сил шляхом множення на відповідну площу.

$\sigma_x (A \cos \theta) + \tau_{xy} (A \sin \theta) = T_x A$

$\tau_{xy} (A \cos \theta) + \sigma_{y} (A \sin \theta) = T_y A$

Скасувавши коефіцієнт$A$, це можна записати в матричному вигляді як

$$\begin{bmatrix} \sigma_x & \tau_{xy} \\ \tau_{xy} & \sigma_y \end{bmatrix} \left \{ \begin{array} {c} {\cos \theta} \\ {\sin \theta} \end{array} \right \} = \left \{ \begin{array} {c} {T_x} \\ {T_y} \end{array} \right \}$$

Малюнок 2: Стрес Коші.

Приклад$\PageIndex{1}$

Розглянемо кругову порожнину, що містить внутрішній тиск$p$. Компонентами вектора тяги є тоді$T_x = -p \cos \theta$,$T_y = -p \sin \theta$. Декартові напруження Коші в матеріалі на кордоні повинні потім задовольняти відносини

$\sigma_x \cos \theta + \tau_{xy} \sin \theta = -p \cos \theta$

$\tau_{xy} \cos \theta + \sigma_y \sin \theta = -p \sin \theta$

В$\theta = 0, \sigma_x = -p, \sigma_y = \tau_{xy} = 0$; в$\theta = \pi /2, \sigma_y = -p, \sigma_x = \tau_{xy} = 0$. Напруга зсуву$\tau_{xy}$ зникає для$\theta = 0$ або$\pi /2$; в модулі 10 буде видно, що нормальні напруги$\sigma_x$ і, отже$\sigma_y$, є основними напруженнями в цих точках.

Малюнок 3: Постійний тиск на внутрішню кругову межу.

Вектор з лівого$(\cos \theta, \sin \theta)$ боку Рівняння 3.2.2 також є$\hat{n}$ вектором напрямку косинусів нормалі до площини, на яку діє тяга, і служить для визначення орієнтації цієї площини. Це матричне рівняння, яке іноді називають відношенням Коші, може бути скорочено

$$[\sigma] \hat{n} = T$$

Дужки тут служать нагадуванням про те, що наголос записується як квадратна матриця рівняння 3.2.2, а не у формі псевдовектора. Це співвідношення служить для визначення поняття напруги як сутності, яка пов'язує тягу (вектор), що діє на довільну поверхню, з орієнтацією поверхні (іншим вектором). Тому напруга має вищий ступінь абстракції, ніж вектор, і технічно є тензором другого рангу. Різниця між векторами (тензорами першого рангу) та тензорами другого рангу проявляється у тому, як вони трансформуються щодо обертань координат, що розглядається в Модулі 10. Як проілюстровано в попередньому прикладі, відношення Коші служить як для визначення напруги, так і для обчислення його величини на границях, де відомі тяги.

Малюнок 4: Декартові компоненти напруги Коші в трьох вимірах.

У трьох вимірах матрична форма напруженого стану, показаного на малюнку 4, є симетричним масивом$\times$ 3 3, отриманим явним продовженням одного в рівнянні 3.2.2:

$$[\sigma] = \sigma_{i,j} = \begin{bmatrix} \sigma_x & \tau_{xy} & \tau_{xx} \\ \tau_{xy} & \sigma_y & \tau_{yx} \\ \tau_{xz} & \tau_{yz} & \sigma_z \end{bmatrix}$$

Елементом в$i^{\th}$ рядку і$j^{th}$ стовпці цієї матриці є наголос на$i^{th}$$j^{th}$ грані в напрямку. Моментна рівновага вимагає, щоб матриця напружень була симетричною, тому порядок індексів позадіагональних напружень зсуву несуттєвий.

Диференціальні рівняння управління

Визначення варіації компонентів напруги як функцій положення всередині тіла, очевидно, є головною метою аналізу напружень. Це тип крайової задачі, часто зустрічається в теорії диференціальних рівнянь, в якій задаються градієнти змінних, а не самі явні змінні. У разі напруги градієнти регулюються умовами статичної рівноваги: напруги не можуть змінюватися довільно між двома точками$A$ і$B$, або матеріал між цими двома точками може бути не в рівновазі.

Для формального розвитку цієї ідеї ми вимагаємо, щоб інтегральне значення$A$ поверхневої тяги Т над поверхнею елемента довільного об'єму$dV$ всередині матеріалу (див. Рис.

$0 = \int_A T dA = \int_A [\sigma] \hat{n} dA$

Тут ми припускаємо відсутність гравітаційних, доцентрових або інших «тілесних» сил, що діють на матеріал в межах об'єму. Поверхневий інтеграл у цьому відношенні може бути перетворений в об'ємний інтеграл за теоремою розбіжності Гауса (Теорема Гаусса стверджує,$X$ що$\int_A X \hat{n} dA = \int_S \nabla X dV$ де скалярна, векторна або тензорна величина. ):

$\int_V \nabla [\sigma] dV = 0$

Оскільки обсяг$V$ довільний, для цього потрібно, щоб integrand дорівнював нулю:

$$\nabla [\sigma] = 0$$

Для декартових задач у трьох вимірах це розширюється до:

$$\begin{array} {c} {\tfrac{\partial \sigma_x}{\partial x} + \tfrac{\partial \tau_{xy}}{\partial y} + \tfrac{\partial \tau_{xz}}{\partial z} = 0} \\ {\tfrac{\partial \tau_{xy}}{\partial x} + \tfrac{\partial \sigma_y}{\partial y} + \tfrac{\partial \tau_{yz}}{\partial z} = 0} \\ {\tfrac{\partial \tau_{xz}}{\partial x} + \tfrac{\partial \tau_{yz}}{\partial y} + \tfrac{\partial \sigma_z}{\partial x} = 0} \end{array}$$

Використовуючи індексні позначення, вони можуть бути записані:

$$\sigma_{ij, j} = 0$$

Або в псевдовекторно-матричній формі ми можемо записати

$$\begin{bmatrix} \tfrac{\partial}{\partial x} & 0 & 0 & 0 & \tfrac{\partial}{\partial z} & \tfrac{\partial}{\partial y} \\ 0 & \tfrac{\partial}{\partial y} & 0 & \tfrac{\partial}{\partial z} & 0 & \tfrac{\partial}{\partial x} \\ 0 & 0 & \tfrac{\partial}{\partial z} & \tfrac{\partial}{\partial y} & \tfrac{\partial}{\partial x} & 0 \end{bmatrix} \left \{ \begin{array} {c} {\sigma_x} \\ {\sigma_y} \\ {\sigma_z} \\ {\tau_{yz}} \\ {\tau_{xz}} \\ {\tau_{xy}} \end{array} \right \} = \left \{ \begin{array} {c} {0} \\ {0} \\ {0} \end{array} \right \}$$

Відзначивши, що диференціальна операторна матриця в дужках є лише перетворенням тієї, що з'явилася в Рівнянні 3.2.7 модуля 8, ми можемо записати це як:

$$L^T \sigma = 0$$

Приклад$\PageIndex{2}$

Неважко придумати функції напруги, які задовольняють рівняння рівноваги; будь-яка константа буде робити, оскільки градієнти напруги тоді будуть однаково нульовими. Підступ полягає в тому, що вони також повинні задовольняти граничним умовам, і це значно ускладнює ситуацію. Пізніше модулі окреслить кілька підходів до безпосереднього вирішення рівнянь, але в деяких простих випадках рішення можна побачити шляхом перевірки.

Малюнок 6: Зразок на розрив.

Розглянемо зразок, що розтягується, що піддається навантаженню$P$, як показано на малюнку 6. Пробне рішення, яке, безумовно, задовольняє рівняння рівноваги, є

$$[\sigma] = \begin{bmatrix} c & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \nonumber$$

де$c$ константа, яку ми повинні вибирати так, щоб задовольнити граничні умови. Для підтримки горизонтальної рівноваги на діаграмі вільного тіла на малюнку 6 (б) відразу видно$cA = P$, що, або$\sigma_x = c = P/A$. Це знайоме відношення було використано в Модулі 1 для визначення напруги, але ми бачимо тут, що його можна розглядати як наслідок міркувань рівноваги, а не як основне визначення.

Вправа$\PageIndex{1}$

Визначте, чи задовольняє рівновагу наступне напружений стан:

$[\sigma] = \begin{bmatrix} 2x^3y^2 & -2x^2y^3 \\ -2x^2y^3 & xy^4 \end{bmatrix}$

Вправа$\PageIndex{2}$

Розробити двовимірну форму декартових рівнянь рівноваги, намалювавши діаграму вільного тіла нескінченно маленького перерізу:

Вправа$\PageIndex{3}$

Скористайтеся діаграмою вільного тіла попередньої проблеми, щоб показати це$\tau_{xy} = \tau_{yx}$.

Вправа$\PageIndex{4}$

Використовуйте підхід діаграми вільного тіла, щоб показати, що в полярних координатах рівняння рівноваги

$\dfrac{\partial \tau_{r \theta}}{\partial r} + \dfrac{1}{r} \dfrac{\partial \sigma_{\theta}}{\partial \theta} + 2 \dfrac{\tau_{r \theta}}{r} = 0$

Вправа$\PageIndex{5}$

Розробити наведені вище рівняння рівноваги в полярних координатах шляхом перетворення декартових рівнянь за допомогою

$x = r \cos \theta$

$y = r \sin \theta$

Вправа$\PageIndex{6}$

Функція напружень Ейрі$\phi (x, y)$ визначається таким чином, що декартові напруги Коші