13: Тригонометрія

Last updated
Save as PDF

Page ID: 31976

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Тригонометрія стосується кутів і довжин трикутників. На малюнку A.1 показаний прямокутний трикутник та умовні позначення його кутів, сторін та кутів. Далі ми припускаємо, що всі трикутники мають принаймні один прямий кут (90 градусів або π/2), оскільки всі площинні трикутники можуть бути розсічені на два прямокутні трикутники.

Малюнок\(\PageIndex{1}\): Зліва: Прямокутний трикутник із загальними позначеннями. Праворуч: Тригонометричні відносини на одиничному колі та кутах, що відповідають чотирьом квадрантам.

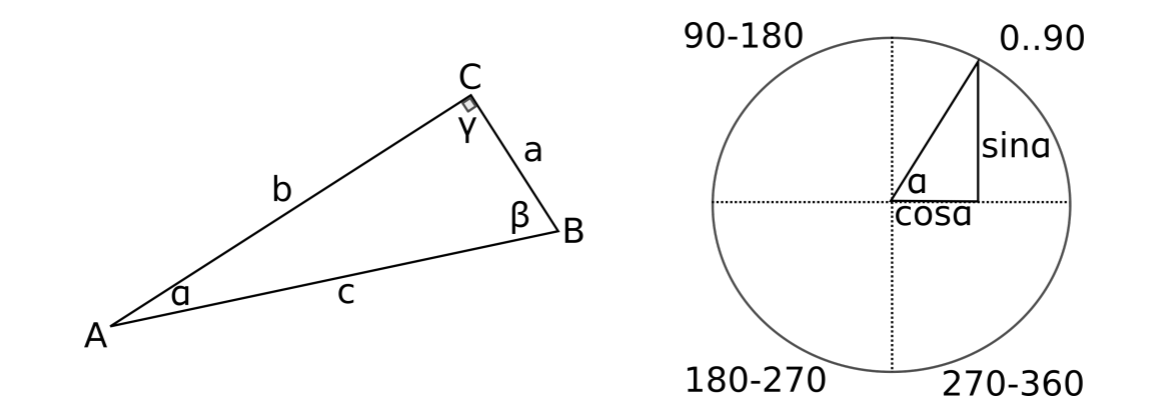
Сума всіх кутів у будь-якому трикутнику дорівнює 180 градусам або 2π, або

\[\alpha +\beta +\gamma =180^{\circ}\]

Якщо трикутник прямокутний, співвідношення між ребрами a, b і c, де c - ребро, протилежне прямому куту, дорівнює

\[a^{2}+b^{2}=c^{2}\]

Взаємозв'язок між кутами та довжинами ребер фіксується тригонометричними функціями:

\[\sin\alpha =\frac{opposite}{hypothenuse}=\frac{a}{c}\]

\[\cos\alpha =\frac{adjacent}{hypothenuse}=\frac{b}{c}\]

\[\tan\alpha =\frac{opposite}{adjacent}=\frac{\sin\alpha }{\cos\alpha }=\frac{a}{b}\]

Тут гіпотеноз - це сторона трикутника, протилежна прямому куту. Сусідні і протилежні розташовуються щодо певного кута. Наприклад, на малюнку 13.1 прилеглим кутом α є сторона b, а протилежна α - ребро a.

Відносини між одним кутом і довжинами ребер фіксуються законом косинусів:

\[a^{2}=b^{2}+c^{2}-2bc\cos\alpha \]