1.1: Одновимірна деформація

Розглянемо призматичну, рівномірну по товщині стрижень або балку початкової довжини$l_o$. Стрижень фіксується на одному кінці і піддається зусиллям розтягування (рис. ($\PageIndex{1}$)) на іншому кінці. Струм, деформована довжина позначається$l$. Питання в тому, чи є результуюче поле деформації однорідним чи ні. Поняття однорідності в механіці означає незалежність рішення від системи просторових координат, осі стрижня в даному випадку. Можна показати, що якщо крива напруження-деформація матеріалу опукла або лінійна, стрижень деформується рівномірно і всередині стрижня розвивається однорідний стан деформацій і напружень. Це означає, що місцеві та середні штами однакові, і деформацію можна визначити, враховуючи загальну довжину. Зсув на нерухомому$x = 0$ кінці стрижня дорівнює нулю,$u(x = 0)$ а зміщення кінця дорівнює

$$u(x = l) = l − l_o \label{1.1.1}$$

Деформація визначається як відносне зміщення. Відносно чого? Початкова, поточна довжина або щось інше? Визначення штаму просте, але в той же час неунікальне.

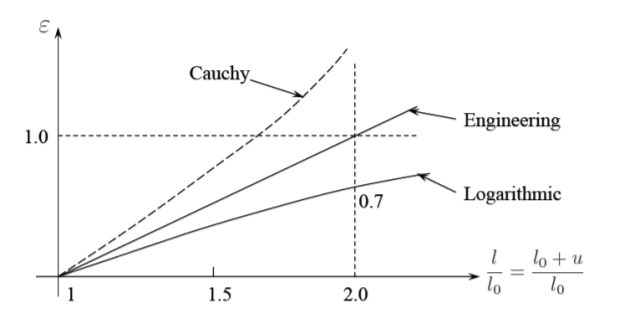
$$\epsilon \buildrel \rm {def} \over{=} \frac{l − l_o}{l_o} \text{ Engineering Strain} \label{1.1.2}$$

$$\epsilon \buildrel \rm {def} \over{=} \frac{1}{2} \frac{l^2 − l_o^2}{l^2} \text{ Cauchy Strain} \label{1.1.3}$$

$$\epsilon \buildrel \rm {def} \over{=} \ln \frac{l}{l_o} \text{ Logarithmic Strain} \label{1.1.4}$$

Кожне з вищезазначених трьох визначень задовольняє основну вимогу, що деформація зникає, коли$l = l_o$ або$u = 0$ що деформація в зростаючій функції переміщення$u$.

Розглянемо граничний випадок рівняння\ ref {1.1.1} для малих переміщень$\frac{u}{l_o} \ll 1$, для яких$l_o+l \approx 2l_o$ у Equation\ ref {1.1.3}. Потім штам Коші стає

$$\epsilon = \frac{l − l_o}{l_o} \frac{l + l_o}{2l_o} \cong \frac{l − l_o}{l_o} \frac{2l}{2l_o} \cong \frac{l − l_o}{l_o} \label{1.1.5}$$

Таким чином, при малих деформаціях штам Коші зводиться до інженерної деформації. Аналогічно, розширюючи вираз для логарифмічної деформації, Equation\ ref {1.1.4} у рядах Тейлора навколо$l − l_o \cong 0$,

$$\left. \ln \frac{l}{l_o} \right|_{l/l_o=1} \cong \frac{l − l_o}{l_o} - \frac{1}{2} \left( \frac{l + l_o}{l_o} \right)^2 + \ldots \approx \frac{l − l_o}{l_o}$$

видно, що логарифмічна деформація зводиться до інженерної деформації.

Графіки$\epsilon$ проти$\frac{l}{l_o}$ відповідно до Рівняння\ ref {1.1.2} -\ ref {1.1.4} показані на рисунку ($\PageIndex{1}$).

Рисунок$\PageIndex{1}$: Порівняння трьох визначень одновісної деформації.

Неоднорідне поле деформації

Деформація повинна бути визначена локально, а не для всієї конструкції. Розглянемо нескінченно малий елемент$dx$ в несформованої конфігурації, рис$\PageIndex{2}$. Після деформації стає довжина вихідного матеріалу елемента$dx + du$. Потім інженерна деформація

$$\epsilon_{\text{eng}} = \frac{(dx + du) − dx}{dx} = \frac{du}{dx} \label{1.1.7}$$

Просторова похідна поля зміщення називається градієнтом зміщення$\boldsymbol{F} = \frac{du}{dx}$. Для одновісного стану деформація - це просто градієнт зсуву. Це не вірно для загального 3-D випадку.

Малюнок$\PageIndex{2}$: Неформований і деформований елемент в однорідному і неоднорідному полі деформації в штанзі.

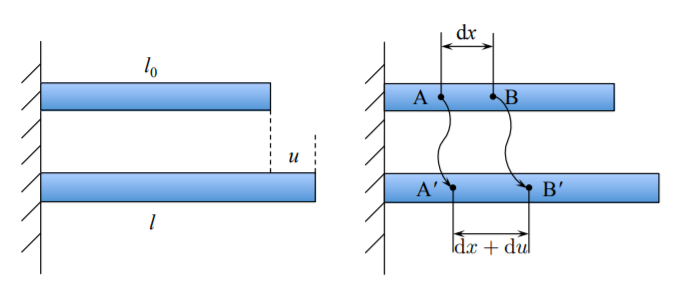
Місцевий штам Коші отримують шляхом прийняття відносних значень різниці квадрата довжин. Як показано в Equation\ ref {1.1.5}, для того, щоб деформація Коші зменшилася до інженерної деформації, в визначення необхідно ввести коефіцієнт 2. Таким чином

$$\epsilon_c = \frac{1}{2} \frac{(dx + du)^2 − dx^2}{dx^2} = \frac{du}{dx} + \frac{1}{2} \left( \frac{du}{dx} \right)^2$$

або$\epsilon_c = \boldsymbol{F} + \frac{1}{2} \boldsymbol{F}^2$. Для малих градієнтів зміщення,

$$\epsilon_c = \epsilon_{\text{eng}}$$