1.2: Розширення до 3-D корпусу
- Page ID
- 33095
Рівняння (1.1.7) можна переписати в альтернативному вигляді
\[ d u = \epsilon d x\]
Розглянемо евклідієвий простір і позначити\(\boldsymbol{x} = \{x_1, x_2, x_3\}\) або\(x_i\) вектор, що представляє положення родової точки тіла. У загальному тривимірному випадку зміщення матеріальної точки також є вектором з компонентами\(\boldsymbol{u} = \{u_1, u_2, u_3\}\) або\(u_i\) де\(i = 1, 2, 3\). Нагадаємо, що приріст функції трьох змінних є сумою трьох складових.
\[ d u_1(x_1, x_2, x_3) = \frac{\partial u_1}{ \partial x_1} d x_1 + \frac{\partial u_1}{ \partial x_2} dx_2 + \frac{\partial u_1}{ \partial x_3} d x_3\]
Загалом, складовими вектора приросту зміщення є
\[ du_i(x_i) = \frac{\partial u_i}{ \partial x_1} d x_1 + \frac{\partial u_i}{ \partial x_2} d x_2 + \frac{\partial u_i}{ \partial x_3} d x_3 = \sum_{j=1}^3 \frac{\partial u_i}{ \partial x_j} d x_j\]
де\(j\) повторюється - так званий індекс «пустушки». Градієнт зміщення
\[\boldsymbol{F} = \frac{\partial u_i}{ \partial x_j}\]
не є симетричним тензором. Він також містить терміни обертання жорсткого тіла. Це можна показати, переписавши вираз for\(\boldsymbol{F}\) в еквівалентній формі
\[\frac{\partial u_i}{ \partial x_j} = \frac{1}{2} \left(\frac{\partial u_i}{ \partial x_j} + \frac{\partial u_j}{ \partial x_i}\right) + \left(\frac{1}{2}\frac{\partial u_i}{ \partial x_j} - \frac{\partial u_j}{ \partial x_i}\right) \label{1.2.5}\]
Тензор деформації\(\epsilon_{ij}\) визначається як «симетрична» частина градієнта зсуву, який є першим членом у Equation\ ref {1.2.5}.
\[\epsilon_{ij} = \frac{1}{2} \left(\frac{\partial u_i}{ \partial x_j} + \frac{\partial u_j}{ \partial x_i}\right) \label{1.2.6}\]
Тепер міняємо (транспонуємо) індекси\(i\) і\(j\) в Equation\ ref {1.2.6}:
\[\epsilon_{ji} = \frac{1}{2} \left(\frac{\partial u_j}{ \partial x_i} - \frac{\partial u_i}{ \partial x_j}\right) \label{1.2.7}\]
Перший член у Equation\ ref {1.2.7} такий самий, як і другий член у Equation\ ref {1.2.6}. І другий член у Equation\ ref {1.2.7} ідентичний першому члену в Equation\ ref {1.2.6}. Тому тензор деформації симетричний.
\[\epsilon_{ij} = \epsilon_{ji}\]
Причина введення властивостей симетрії тензора деформації буде пояснена далі в цьому розділі. Другі члени в Equation\ ref {1.2.5} називають тензором спіна\(\omega_{ij}\)
\[\omega_{ij} = \frac{1}{2} \left(\frac{\partial u_i}{ \partial x_j} + \frac{\partial u_j}{ \partial x_i}\right)\]
Використовуючи подібні аргументи, як і раніше, легко побачити, що тензор спина антисиметричний.
\[w_{ij} = -w_{ji} \label{1.2.10}\]
З визначення випливає, що діагональні долі тензора спіна дорівнюють нулю, наприклад\(w_{11} = −w_{11} = 0\). Компонентами тензора деформації є:
- \(i = 1, j = 1\)\[ \epsilon_{11} = \frac{1}{2} \left(\frac{\partial u_1}{ \partial x_1} + \frac{\partial u_1}{ \partial x_1}\right) = \frac{\partial u_1}{ \partial x_1} \label{1.2.11}\]
- \(i = 2, j = 2\)\[\epsilon_{22} = \frac{\partial u_2}{ \partial x_2}\]
- \(i = 3, j = 3\)\[ \epsilon_{33} = \frac{\partial u_3}{ \partial x_3}\]
- \(i = 1, j = 2\)\[\epsilon_{12} = \epsilon_{21} = \frac{1}{2} \left(\frac{\partial u_1}{ \partial x_2} + \frac{\partial u_2}{ \partial x_1}\right)\]
- \(i = 2, j = 3\)\[ \epsilon_{23} = \epsilon_{32} = -\frac{1}{2} \left(\frac{\partial u_2}{ \partial x_3} + \frac{\partial u_3}{ \partial x_2}\right)\]
- \(i = 3, j = 1\)\[ \epsilon_{31} = \epsilon_{13} = -\frac{1}{2} \left(\frac{\partial u_3}{ \partial x_1} + \frac{\partial u_1}{ \partial x_3}\right)\]
Для геометричної інтерпретації тензора деформації та спінового тензора розглянемо нескінченно малий квадратний елемент, який\((dx_1, dx_2)\) піддається декільком простим випадкам деформації. Часткові похідні замінюються скінченними відмінностями, наприклад
\[\frac{\partial u_1}{ \partial x_1} = \frac{\Delta u_1}{\Delta x_1} = \frac{u_1(x_1) - u_1(x_1 +h)}{h}\]
Переклад жорсткого тіла
Уздовж\(x_1\) осі:
\[u_1(x_1) = u_1(x_1 + h)\]
\[u_2 = u_3 = 0\]
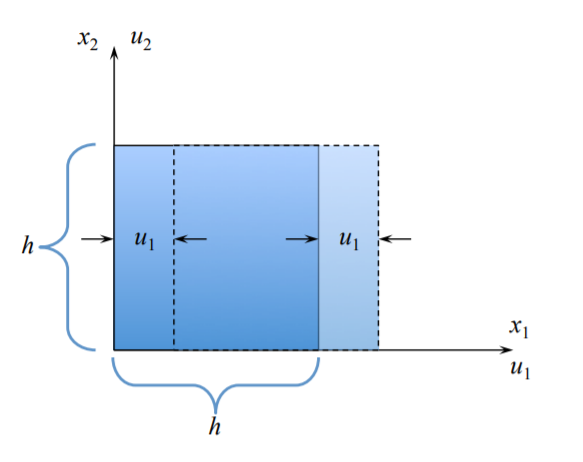
З\ ref {1.2.11} випливає, що відповідний компонент деформації зникає,\(\epsilon_{11} = 0\). Перша складова тензора спіна дорівнює нулю з визначення,\(\omega_{11} = 0\).
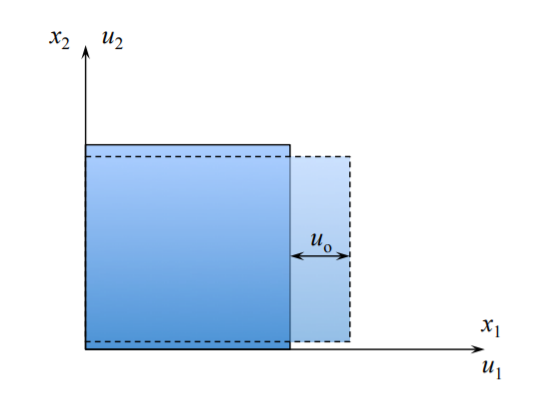
Розширення вздовж\(x_1\) осі
За адресою\(x_1\):\(u_1 = 0\).
За адресою\(x_1 + h\):\(u_1 = u_o\).
Відповідний штам є\(\epsilon_{11} = \frac{u_o}{h}\).
Чистий зсув на\(x_1x_2\) площині
При\(x_1 = 0\) і\(x_2 = 0\):\(u_1 = u_2 = 0\)
При\(x_1 = h\) і\(x_2 = 0\):\(u_1 = 0\) і\(u_2 = u_o\)
При\(x_1 = 0\) і\(x_2 = h\):\(u_1 = u_o\) і\(u_2 = 0\)
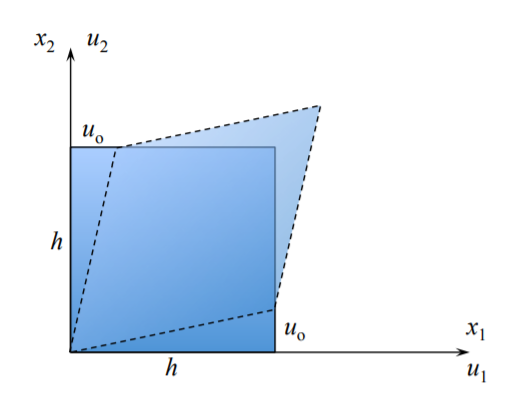
З Рівняння\ ref {1.2.10} і Рівняння\ ref {1.2.6} випливає, що:
\[\epsilon_{12} = \frac{1}{2} \left( \frac{u_o}{h} +\frac{u_o}{h}\right) = \frac{u_o} {h}\]
\[\omega_{12} = \frac{1}{2} \left( \frac{u_o}{h} − \frac{u_o}{h}\right) = 0\]
Отримана деформація являє собою зміну кутів початкового прямолінійного елемента.
Жорстке обертання тіла
При\(x_1 = 0\) і\(x_2 = 0\):\(u_1 = u_2 = 0\)
При\(x_1 = h\) і\(x_2 = 0\):\(u_1 = 0\) і\(u_2 = u_o\)
При\(x_1 = 0\) і\(x_2 = h\):\(u_1 = -u_o\) і\(u_2 = 0\)
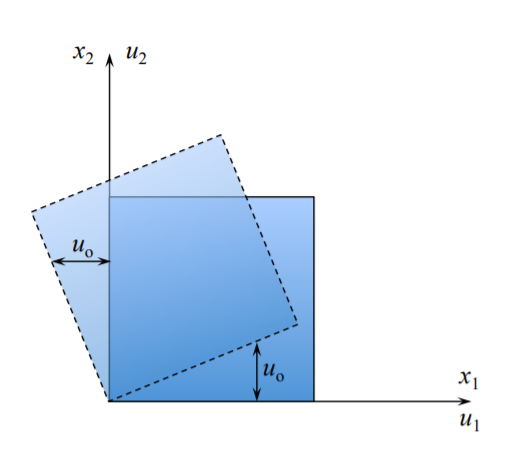
Зміна знака\(u_1\) at\(x_1 = 0\) і from to\(-u_o\) призводить\(x_2 = h\)\(u_o\) до ненульового спина, але нульової деформації
\[\epsilon_{12} = \frac{1}{2} \left( \frac{u_o}{h} + \left(− \frac{u_o}{h}\right)\right) = 0\]
\[\omega_{12} = \frac{1}{2} \left( \frac{u_o}{h} + \left(− \frac{u_o}{h}\right)\right) = \frac{u_o} {h}\]
Останній приклад дає пояснення, чому тензор деформації був визначений як симетрична частина градієнта зміщення. Фізика диктує, що трансляція і обертання твердого тіла не повинні викликати будь-які деформації в матеріальний елемент. При обертанні жорсткого тіла градієнти переміщення не дорівнюють нулю. Тензор деформації, що визначається як симетрична частина градієнта зміщення, усуває ефект обертання в стані деформації в тілі. Іншими словами, деформація описувала зміну довжини і кутів при віджиманні, обертанні елемента.
