1.8: Розширена форма співвідношення деформації-зміщення
- Page ID
- 33050
Виведши геометричні відносини в тензоріальних позначення, рівняння (1.7.10) і (1.7.11) будуть перезаписані в систему координат (x, y) і фізична інтерпретація буде дана кожному семестру. Розглянемо спочатку (1.7.11)
\[\alpha = 1, \beta = 1 \; x_1 = x, \; \epsilon_{xx}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{x}^{\circ}}{\partial x} + \frac{\partial u_{x}^{\circ}}{\partial x} \right) = \frac{\partial u_{x}^{\circ}}{\partial x} \]
\[\alpha = 2, \beta = 2 \; x_2 = y, \; \epsilon_{xx}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{y}^{\circ}}{\partial y} + \frac{\partial u_{y}^{\circ}}{\partial y} \right) = \frac{\partial u_{y}^{\circ}}{\partial y} \]
\[\alpha = 1, \beta = 2 \; x_1 = x, x_2 = y, \; \epsilon_{xy}^{\circ} = \frac{1}{2} \left( \frac{\partial u_{x}^{\circ}}{\partial y} + \frac{\partial u_{y}^{\circ}}{\partial x} \right) \]
\(\epsilon_{yy}^{\circ}\)Компоненти\(\epsilon_{xx}^{\circ}\) і позначають штами середньої поверхні пластини в\(y\) напрямках\(x\) і, шанобливо. Мембранні деформації обумовлені накладеними зміщеннями або силами мембрани, прикладеної до країв. У теорії малого прогину пластин навантаження поперечного тиску не призведе до деформацій мембрани. Навпаки, мембранні деформації дійсно розвиваються в теорії помірно великого прогину пластин внаслідок поперечного навантаження. Ця тема буде розглянута пізніше в розділі 6.
Третім компонентом тензора деформації є деформація зсуву в площині\(\epsilon_{xy}^{\circ}\). Вона являє собою зміну кутів в площині плити за рахунок навантаження на зсув по краях. Геометрична інтерпретація тензора деформації мембрани подібна до тієї, що наведена для тензора загальної деформації на малюнках (1.2.2) та (1.2.3).
Тензор кривизни\(\kappa_{\alpha \beta}\) вимагає ретельного пояснення. Розглянемо нескінченно малий відрізок ds кривої і вписуємо в нього коло миттєвого радіуса ρ, Рисунок (\(\PageIndex{1}\)). Тоді
\[ds = \rho d\theta \]
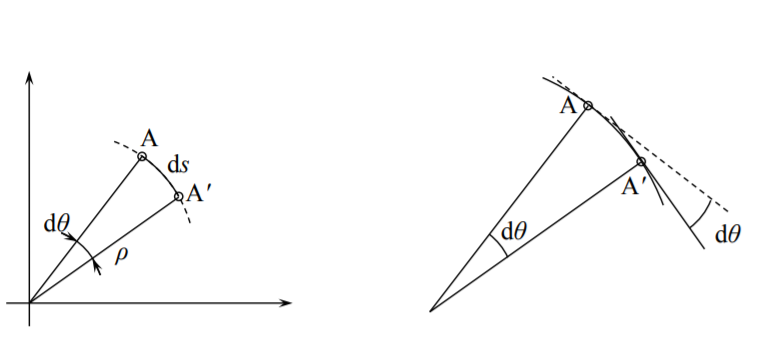
Математично кривизна будь-якої лінії\(\kappa\) - це зміна нахилу при русі по кривій
\[\kappa \buildrel \rm {def} \over{=} \frac{d\theta }{ds} \label{1.8.5}\]
Порівнюючи рівняння\ ref {1.8.5} з рівнянням (1.7.2), кривизна в\([ \frac{1}{m} ]\) є взаємністю радіуса кривизни\(\kappa = \frac{1}{\rho}\). Першою складовою тензора кривизни, визначеного рівнянням (1.7.10), є
\[\alpha = 1, \beta = 1 \; x_1 = x \; \kappa_{xx} = -\frac{\partial^2 w}{\partial x^2} = -\frac{\partial}{\partial x} \left( \frac{\partial w}{\partial x} \right) = \frac{\partial}{\partial x} ( - \theta_{x})\]
Це буде єдиною складовою тензора кривизни, якщо пластина піддається так званому циліндричному вигину.
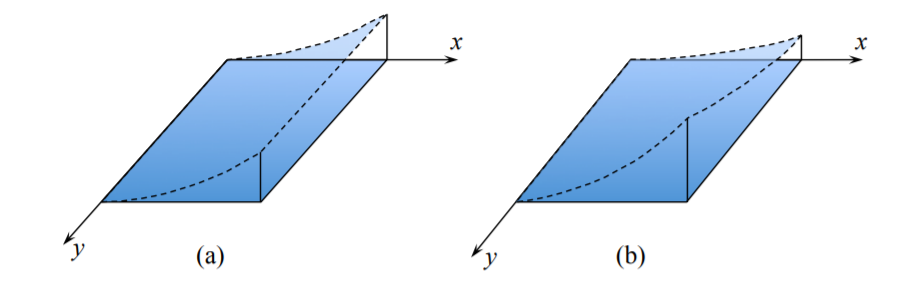
Інтерпретація\(\kappa_{yy}\) складових тензора кривизни
\[\alpha = 2, \beta = 2 \; x_2 = y \; \kappa_{yy} = -\frac{\partial^2 w}{\partial y^2} = -\frac{\partial}{\partial y} ( - \theta_{y})\]
схоже, як і раніше. Більш цікавим є змішаний компонент тензора кривизни
\[\alpha = 1, \beta = 2 \; x_1 = x, x_2 = y \; \kappa_{xy} = -\frac{\partial^2 w}{\partial x \partial y} = -\frac{\partial}{\partial y} ( - \theta_{x})\]
Для виявлення\(\kappa_{xy}\) потрібно перевірити, чи нахил в одному напрямку, скажімо,\(\theta_x\) змінюється вздовж другого\(y\) -напрямку. Це не для циліндричного вигину, рис. (1.4.2 (а)). Але якщо це відбувається, то пластина скручується, як показано на малюнку (1.4.2 (b)). Тому компонент\(\kappa_{xy}\) називається твіст.
Важливим параметром, що відрізняє ці класи деформованої форми пластини, є гаусова кривизна,\(\kappa_{G}\). Гаусова кривизна визначається як добуток двох основних викривлень
\[\kappa_{G} = \kappa_I\kappa_{II}\]
Кривизна є тензором, тому її компоненти змінюються, обертаючи систему координат на кут\(\psi\) до нового напрямку (x\ prime, y\ prime). Є один такий кут,\(\psi_p\) при якому скручуються компоненти зникають. Решта діагональні складові називаються основною кривизною. Повне охоплення формул перетворення векторів і тензорів представлено в Recitation 2. Використовуючи ці результати, гауссова кривизна може бути виражена через складові тензора кривизни
\[\kappa_{G} = \kappa_{xx} \kappa_{yy} − \kappa_{xy}^2\]
Для циліндричного згинання скручування ρxy, а також одна з основних кривизн зникає так, що гаусова кривизна дорівнює нулю. Ознакою гауссовой кривизни розрізняють три види деформованої пластини: чаша, циліндр і сідло, рис. (\(\PageIndex{3}\)).
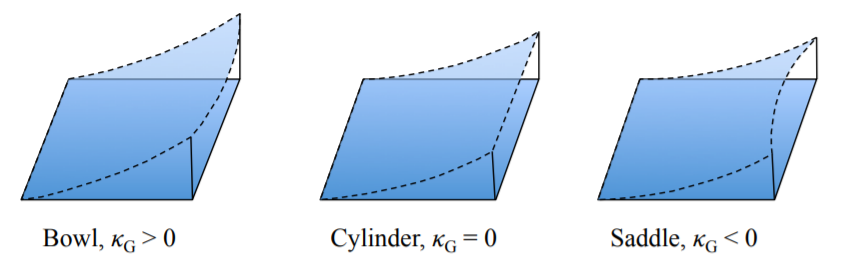
Розгляд гаусової кривизни вносить важливі спрощення у формулюванні та застосуванні енергетичного методу в будівельній механіці. Окрема лекція буде присвячена цій темі.
