2.6: Прості системи

Last updated
Save as PDF

Page ID: 33238

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Системи маніпулюють сигналами.
Є кілька простих систем, які виконуватимуть прості функції за сигналами. Приклади включають посилення (або загасання), реверсування часу, затримку та диференціацію/інтеграцію.

Системи маніпулюють сигналами, створюючи вихідні сигнали, отримані з їх входів. Чому наступні класифікуються як «прості», стане очевидним лише до кінця курсу.

Джерела

Джерела видають сигнали, не маючи входу. Нам подобається думати про них як про керовані параметри, такі як амплітуда та частота. Прикладами можуть бути осцилятори, які виробляють періодичні сигнали, такі як синусоїди та квадратні хвилі, та генератори шуму, які дають сигнали з нестабільними формами хвиль (докладніше про шум згодом). Просто написання виразу для сигналів, які вони виробляють, визначає джерела. Генератор синусоїди може бути вказаний за допомогою:

\[y(t) = A\sin (2\pi f_{0}t)u(t) \nonumber \]

Вищенаведене рівняння говорить про те, що джерело був включений при t = 0 для отримання синусоїди амплітуди A і частоти f ₀.

Підсилювачі

Підсилювач множить свій вхід на постійну, відому як посилення підсилювача.

\[y(t) = Gx(t) \nonumber \]

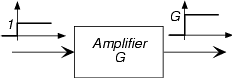
Коефіцієнт посилення може бути позитивним або негативним (якщо негативний, ми б сказали, що підсилювач інвертує свій вхід) і його величина може бути більше одного або менше одиниці. Якщо менше одиниці, підсилювач насправді слабшає. Реальний приклад підсилювача - ваш домашній стерео. Ви керуєте посиленням, повертаючи регулятор гучності.

Затримка

Система служить затримкою часу, коли вихідний сигнал дорівнює вхідному сигналу в більш ранній час.

\[y(t) = x(t-\tau ) \nonumber \]

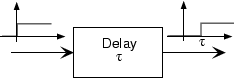
Тут τ - це затримка. Спосіб зрозуміти цю систему полягає в тому, щоб зосередитися на початку часу: Вихід в час t = τ дорівнює входу в час t = 0 Таким чином, якщо затримка позитивна, вихід з'являється пізніше, ніж вхід, і побудова вихідних даних становить зміщення вхідного графіка вправо. Затримка може бути негативною, і в цьому випадку ми говоримо, що система просуває свій вхід. Такі системи важко побудувати (вони повинні були б виробляти значення сигналу, отримані від того, що буде вхід), але у нас буде привід вчасно просунути сигнали.

Час розвороту

Тут вихідний сигнал дорівнює вхідному сигналу, перевернутому про час походження.

\[y(t) = x(-t) \nonumber \]

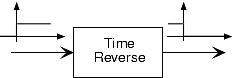
Знову ж таки, такі системи важко побудувати, але поняття зміни часу часто зустрічається в системах зв'язку.

Вправа\(\PageIndex{1}\)

Згадувалося раніше питання про те, чи має значення впорядкування систем. Іншими словами, якщо у нас є дві системи в каскаді, чи залежить вихід від того, який приходить першим? Визначте, чи має значення порядок для каскаду підсилювача та затримки, а також для каскаду системи часового розвороту та затримки.

Рішення

У першому випадку порядок не має значення; у другому це робить. «Затримка» означає t → t - τ. «Час-реверс» означає t → -t.

Випадок 1

\[y(t) = Gx(t-\tau ) \nonumber \]

Те, як ми застосовуємо посилення і затримку сигналу, дає той же результат.

Випадок 2

Час зворотного, потім затримка:

\[y(t) = x\left ( - (t-\tau )\right ) = x(-t+\tau ) \nonumber \]

Затримка, потім зворотний час:

\[y(t) = x\left ( (-t)-\tau )\right ) \nonumber \]

Похідні системи та інтегратори

Системи, які виконують обчислювальні операції на своїх входах, можуть створювати сигнали, значно відрізняються від присутніх на вході. Похідні системи працюють простим способом: система першої похідної матиме відношення «вхід-вихід»

\[y(t) = \frac{\mathrm{d} }{\mathrm{d} t}x(t) \nonumber \]

Інтегральні системи мають ускладнення, що межі інтеграла повинні бути визначені. Це угода теорії сигналів, що елементарна інтегральна операція має нижню межу\(-\infty \nonumber \) і що значення всіх сигналів при\(t = -\infty \nonumber \) рівному нулю. Простий інтегратор мав би відношення «вхід-вихід»:

\[y(t) = \int_{-\infty }^{t}x(\alpha )d\alpha \nonumber \]

Лінійні системи

Лінійні системи - це клас систем, а не мають певне співвідношення вхід-вихід. Лінійні системи складають основу теорії систем і є найважливішим класом систем у комунікаціях. Вони мають властивість, що коли вхід виражається у вигляді зваженої суми компонентних сигналів, вихід дорівнює тій же зваженій сумі виходів, вироблених кожним компонентом. Коли S (•) лінійний,

\[S\left ( G_{1}x_{1}(t)+ G_{2}x_{2}(t) \right ) = G_{1}S(x_{1}(t))+ G_{2}S(x_{2}(t)) \nonumber \]

для всіх варіантів сигналів і підсилень.

Цією загальною властивістю відношення вхід-виводу можна маніпулювати, щоб вказати конкретні властивості, які поділяються всіма лінійними системами.

\[S(Gx(t)) = GS(x(t)) \nonumber \]

Розмовність підсумовує цю властивість - «Подвоїти вхід, ви подвоїте вихід». Зауважте, що ця властивість узгоджується з альтернативними способами вираження змін посилення: Оскільки 2x (t) також дорівнює x (t) +x (t), визначення лінійної системи забезпечує однаковий вихід незалежно від того, який з них використовується для вираження заданого сигналу.

\[S(0) = 0 \nonumber \]

Якщо вхід однаково нульовий за весь час, вихід лінійної системи повинен дорівнювати нулю. Це властивість випливає з простого виведення:

\[S(0) = S(x(t)-x(t)) = S(x(t)) - S(x(t)) = 0 \nonumber \]

Те, чому лінійні системи так важливі, пов'язано не тільки з їх властивостями, які розкриваються протягом усього цього курсу, але і тому, що вони піддаються відносно простому математичному аналізу. Сказав інший спосіб: «Це єдині системи, які ми ретельно розуміємо!»

Ми можемо знайти вихід будь-якої лінійної системи на складний вхід, розклавши вхід на прості сигнали. Вищенаведене рівняння говорить про те, що коли система лінійна, її вихід на розкладений вхід - це сума виходів до кожного входу. наприклад, якщо,

\[x(t) = e^{-t} + \sin (2\pi f_{0}t) \nonumber \]

Вихід S (x (t)) будь-якої лінійної системи дорівнює

\[y(t) = S(e^{-t}) + S(\sin (2\pi f_{0}t)) \nonumber \]

Час-інваріантні системи

Системи, які не змінюють своє співвідношення вхід-виводу з часом, вважаються інваріантними у часі. Математичний спосіб заявити цю властивість полягає у використанні концепції затримки сигналу, описаної вище в простих системах.

\[(y(t) = S(x(t))) \Rightarrow (y(t-\tau ) = S(x(t-\tau ))) \nonumber \]

Якщо ви затримаєте (або просуваєте) вхід, вихід аналогічно затримується (розширено). Таким чином, інваріантна система реагує на вхід, який ви можете поставити завтра так само, як вона реагує на той самий вхід, застосований сьогодні; сьогоднішній вихід просто затримується, щоб відбутися завтра.

Колекція лінійних, інваріантних в часі систем є найбільш детально вивченими системами. Значна частина розглянутої тут теорії сигналів і теорії систем зосереджується на таких системах. Наприклад, електричні ланцюги є, здебільшого, лінійними і інваріантними за часом. Нелінійних предостатньо, але охарактеризувати їх так, щоб можна було передбачити їх поведінку для будь-якого входу, залишається невирішеною проблемою.