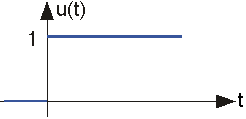2.2: Стихійні сигнали
- Page ID
- 33262
- Складні сигнали можуть бути побудовані з елементарних сигналів, включаючи складні експоненціальні, одиничний крок, імпульс і т.д.
- Дізнатися про стихійні сигнали.
Елементарні сигнали - це будівельні блоки, за допомогою яких ми будуємо складні сигнали. За визначенням, елементарні сигнали мають просту структуру. Саме те, що ми маємо на увазі під «структурою сигналу», розгорнеться в цьому розділі курсу. Сигнали - це не що інше, як функції, визначені стосовно якоїсь незалежної змінної, яку ми вважаємо часом здебільшого. Дуже цікаві сигнали - це не функції виключно часу; одним чудовим прикладом якого є зображення. Для нього незалежними змінними є x і y (двовимірний простір). Відеосигнали - це функції трьох змінних: двох просторових вимірів і часу. На щастя, більшість ідей, що лежать в основі сучасної теорії сигналів, можуть бути прикладом одновимірних сигналів.
синусоїди
Мабуть, найпоширенішим реальним сигналом є синусоїда.
\[s(t) = A\cos (2\pi f_{0}t+\varphi ) \nonumber \]
Для цього сигналу,це його амплітуда,його частоти, ійого фаза.
Складні експоненціальні
Найважливішим сигналом є комплексно-значний, складний експоненціальний.
\[s(t) = Ae^{i(2\pi f_{0}t+\varphi )}\\ s(t) = Ae^{i\varphi }e^{i2\pi f_{0}t} \nonumber \]
Тут,
\[Ae^{i\varphi } \: is\: the\: signal's\: \textbf{complex amplitude} \nonumber \]
Розглядаючи комплексну амплітуду як комплексне число в полярній формі, її величина - амплітуда А, а кут - фазою сигналу. Комплексна амплітуда також відома як фасор. Складний експоненціальний не може бути додатково розкладений на більш елементарні сигнали, і є найважливішим сигналом в електротехніці! Математичні маніпуляції спочатку здаються складнішими, оскільки вводяться складнозначні числа. Насправді, на початку ХХ століття математики вважали, що інженери не будуть достатньо витонченими, щоб обробляти складні експоненціальні показники, хоча вони значно спростили вирішення проблем схеми. Штайнметц ввів складні експоненціальні показники в електротехніку і продемонстрував, що «прості» інженери можуть використовувати їх для хорошого ефекту і навіть отримати правильні відповіді! Див. розділ Комплексні числа для огляду комплексних чисел та комплексної арифметики.
Комплексна експоненціальна визначає поняття частоти: це єдиний сигнал, який містить лише одну частотну складову. Синусоїда складається з двох частотних складових: одна на частоті f 0, а інша при -f 0.
Це розкладання синусоїди простежується до відношення Ейлера.
\[\cos (2\pi ft) = \frac{e^{i2\pi ft}+e^{-(i2\pi ft)}}{2}\\ \sin (2\pi ft) = \frac{e^{i2\pi ft}-e^{-(i2\pi ft)}}{2i}\\ e^{i2\pi ft} = cos (2\pi ft)+i\: sin (2\pi ft) \nonumber \]
Таким чином, складний експоненціальний сигнал може бути записаний у терміні його реальної та уявної частин, використовуючи відношення Ейлера. Таким чином, синусоїдальні сигнали можуть бути виражені як реальною, так і уявною частиною складного експоненціального сигналу, вибір в залежності від того, чи потрібен косинус або синусоїдальна фаза, або як сума двох комплексних експоненціальних. Ці два розклади математично еквівалентні один одному.
\[A\cos (2\pi ft+\varphi ) = \Re (Ae^{i\varphi }e^{i2\pi ft})\\ A\sin (2\pi ft+\varphi ) = \Im (Ae^{i\varphi }e^{i2\pi ft}) \nonumber \]
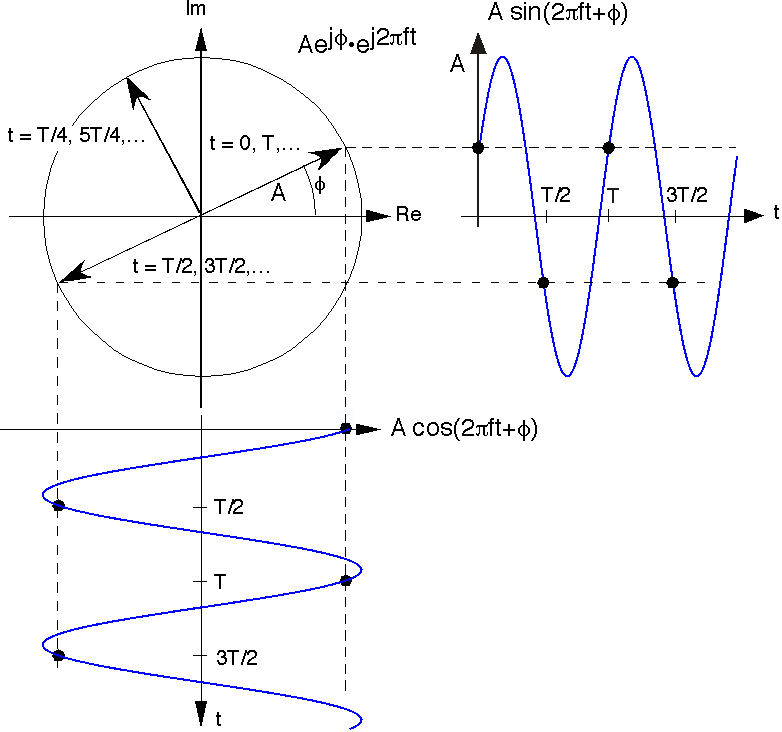
Використовуючи складну площину, ми можемо уявити тимчасові варіації складної експоненції, як показано на малюнку вище. Величина комплексної експоненціальної дорівнює А, а початкове значення експоненціальної комплексу при t = 0 має кут φ. Зі збільшенням часу локус точок, простежуваних комплексною експоненцією, є коло (він має постійну величину A). Кількість разів на секунду ми обходимо коло дорівнює частоті f Час, прийнятий для комплексної експоненціальної, щоб обійти коло один раз відомий як його період T і дорівнює 1/f. Проекції на дійсну та уявну осі обертового вектора, що представляє складний експоненціальний сигнал, є косинусним і синусоїдальним сигналом відношення Ейлера, як зазначено вище.
Реальні експоненціальні
На відміну від складних експоненціальних, які коливаються, реальні експоненціальні розпадаються.
\[s(t) = e^{-\frac{t}{\tau }} \nonumber \]

Величина τ відома як постійна часу експоненції і відповідає часу, необхідному для зменшення експоненції на коефіцієнт 1/e, який приблизно дорівнює 0,368. Гниючий складний експоненціальний є добутком реального і складного експоненціального.
\[s(t) = Ae^{i\varphi }e^{-\frac{t}{\tau }}e^{i2\pi ft}\\ s(t) = Ae^{i\varphi }e^{\left ( -\frac{t}\tau +i2\pi f \right )t} \nonumber \]
У комплексній площині цей сигнал відповідає експоненціальної спіралі. Для таких сигналів ми можемо визначити складну частоту як величину, що множить t.
Крок одиниці
Функція одиниці кроку позначається u (t) і визначається як
\[u(t) = 0\, \, if \,\, t< 0\\ u(t) = 1\, \: if \, \, t> 0 \nonumber \]
Цей сигнал є переривчастим у початку. Його значення на початку не повинно бути визначено, і не має значення в теорії сигналів.
Цей вид сигналу використовується для опису сигналів, які «включаються» раптово. Наприклад, щоб математично представити включення осцилятора, ми можемо записати його як добуток синусоїди та кроку:
\[s(t) = A\sin (2\pi ft)u(t) \nonumber \]
Пульс
Одиничний імпульс описує включення одинично-амплітудного сигналу на тривалість Δ секунд, а потім його вимкнення.
\[p\Delta (t) = 0\; if\; t< 0\\ p\Delta (t) = 1\; if\; 0< t< \Delta \\ p\Delta (t) = 0\; if\; t> \Delta \nonumber \]

Ми виявимо, що це другий за значимістю сигнал в комунікаціях.
Квадратна хвиля
Квадратна хвиля sq (t) - періодичний сигнал, подібний синусоїді. Він теж має амплітуду і період, який необхідно вказати для характеристики сигналу. Згодом ми виявляємо, що синусоїда є більш простим сигналом, ніж квадратна хвиля.