2.4: Дискретні сигнали часу

Last updated
Save as PDF

Page ID: 33263

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Сигнали можуть бути представлені дискретними величинами, а не як функція безперервної змінної.
Ці дискретні сигнали часу не обов'язково повинні приймати значення дійсних чисел.
Багато властивостей безперервних значущих сигналів переносять практично безпосередньо в дискретну область.

Поки що ми розглядали те, що відомо як аналогові сигнали та системи. Математично аналогові сигнали - це функції, що мають безперервні величини як незалежні змінні, такі як простір та час. Сигнали дискретного часу - це функції, визначені на цілих числах; вони є послідовностями. Одним з фундаментальних результатів теорії сигналів будуть деталізовані умови, за яких аналоговий сигнал може бути перетворений в дискретний час і витягнутий без помилок. Цей результат важливий, оскільки сигнали дискретного часу можуть маніпулювати системами, екземплярами яких є комп'ютерні програми. Наступні модулі описують, як практично вся обробка аналогового сигналу може бути виконана за допомогою програмного забезпечення.

Наскільки важливі такі результати, сигнали дискретного часу є більш загальними, охоплюючи сигнали, отримані від аналогових, і сигнали, які не є. Наприклад, символи, що утворюють текстовий файл, утворюють послідовність, яка також є сигналом дискретного часу. Ми також повинні мати справу з такими символічними цінними сигналами та системами.

Як і у випадку з аналоговими сигналами, ми шукаємо способи розкладання реальних дискретних сигналів часу на простіші компоненти. Завдяки такому підходу, що призводить до кращого розуміння структури сигналу, ми можемо використовувати цю структуру для представлення інформації (створення способів представлення інформації за допомогою сигналів) та отримання інформації (отримання інформації, представленої таким чином). Для символічно-значущих сигналів підхід інший: ми розробляємо загальне уявлення всіх символічно-значущих сигналів, щоб ми могли уніфіковано втілити інформацію, яку вони містять. З точки зору представлення інформації найважливішим питанням стає ефективність як для реальних, так і для символічно значущих сигналів; Що є найбільш парсимонійним і компактним способом представлення інформації, щоб її можна було витягти пізніше.

Реальні та комплексні сигнали

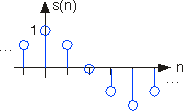
Сигнал дискретного часу символічно представлений у вигляді s (n), де n = {..., -1,0,1...}. Зазвичай ми малюємо сигнали дискретного часу як стовбурові графіки, щоб підкреслити той факт, що вони є функціями, визначеними лише на цілих числах. Ми можемо затримати сигнал дискретного часу цілим числом так само, як і з аналоговими. Відкладена одинична вибірка має вираз

δ (n − м ) δ (n − м )\[\delta (n-m) \nonumber \]

і дорівнює одиниці, коли n = m.

Малюнок 2.4.1 Сигнал косинуса дискретного часу будується у вигляді стовбурової ділянки. Чи можете ви знайти формулу для цього сигналу?

Складні експоненціальні

Найважливішим сигналом є, звичайно ж, складна експоненціальна послідовність.

\[s(n) = e^{i2\pi fn} \nonumber \]

синусоїди

Синусоїди дискретного часу мають очевидну форму

\[s(n) = A\cos (2\pi fn+\varphi ) \nonumber \]

На відміну від аналогових складних експоненціальних та синусоїдів, які можуть мати свої частоти будь-якого реального значення, частоти їх дискретних аналогів дають унікальні форми хвиль лише тоді, коли f лежить в інтервалі (-½). Цю властивість можна легко зрозуміти, зазначивши, що додавання цілого числа до частоти експоненціального комплексу дискретного часу не впливає на значення сигналу.

\[e^{i2\pi (f+m)n} = e^{i2\pi fn}e^{i2\pi mn}\\ e^{i2\pi (f+m)n} = e^{i2\pi fn} \nonumber \]

Це випливає з того, що комплексна експоненціальна обчислюється цілим числом, кратним 2π, дорівнює одиниці.

Одиниця зразка

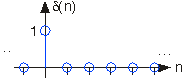
Другим за важливістю сигналом дискретного часу є одиничний зразок, який визначається як

\[\delta (n) = 1\; if\; n=0\\ \delta (n) = 0\; otherwise \nonumber \]

Дослідження графіка сигналу дискретного часу, як і косинусний сигнал, показаний на малюнку 2.4.1, виявляє, що всі сигнали складаються з послідовності затриманих і масштабованих одиничних зразків. Оскільки значення послідовності у кожного цілого числа m позначається s (m) і записується одинична вибірка з затримкою на m

δ (n − м )\[\delta (n-m) \nonumber \]

ми можемо розкласти будь-який сигнал у вигляді суми одиничних зразків, затриманих до відповідного місця та масштабованих за значенням сигналу.

\[s(n) = \sum_{m=-\infty }^{\infty }s(m)\delta (n-m) \nonumber \]

Цей вид розкладання є унікальним для дискретних сигналів часу, і згодом виявиться корисним.

Системи дискретного часу можуть діяти на сигнали дискретного часу способами, подібними до тих, що містяться в аналогових сигналах та системах. Через роль програмного забезпечення в системах дискретного часу, набагато більше різних систем можуть бути передбачені і «побудовані» з програмами, ніж це може бути з аналоговими сигналами. Насправді, спеціальний клас аналогових сигналів може бути перетворений в сигнали дискретного часу, оброблені за допомогою програмного забезпечення, і перетворений назад в аналоговий сигнал, і все це без помилки. Для таких сигналів системи можуть бути легко створені в програмному забезпеченні, з еквівалентними аналоговими реалізаціями важко, якщо не неможливо, розробити.

Символічні сигнали

Ще один цікавий аспект дискретних сигналів часу полягає в тому, що їх значення не повинні бути дійсними числами. У нас є реальні сигнали дискретного часу, такі як синусоїда, але ми також маємо сигнали, які позначають послідовність символів, набраних на клавіатурі. Такі символи, безумовно, не є дійсними числами, і як набір можливих значень сигналу, вони мають невелику математичну структуру, крім того, що вони є членами набору. Більш формально кожен елемент символічного сигналу s (n) приймає одне із значень {a ₁,... a _K}, які містять алфавіт A. Ця технічна термінологія не означає, що ми обмежуємо символи членами англійського або грецького алфавіту. Вони можуть представляти символи клавіатури, байти (8-бітові кількості), цілі числа, які передають добову температуру. Незалежно від того, контролюються програмним забезпеченням чи ні, системи дискретного часу в кінцевому підсумку будуються з цифрових схем, які повністю складаються з елементів аналогових схем. Крім того, передача та прийом дискретних сигналів часу, таких як електронна пошта, здійснюється за допомогою аналогових сигналів та систем. Розуміння того, як дискретно-часові та аналогові сигнали та системи переплітаються, мабуть, є головною метою цього курсу.