Skip to main content
LibreTexts - Ukrayinska

3.3: Рух снаряда

  1. Last updated
  2. Save as PDF
  • Page ID
    75084

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Основні рівняння та параболічний шлях

    Рух снаряда - це форма руху, коли об'єкт рухається параболічним шляхом; шлях, яким слідує об'єкт, називається його траєкторією.

    цілі навчання

    • Оцінити вплив кута і швидкості на траєкторію руху снаряда; вивести максимальну висоту за допомогою переміщення

    Рух снаряда

    Рух снаряда - це форма руху, коли об'єкт рухається в двосторонньому симетричному параболічному шляху. Шляхом, яким слідує об'єкт, називається його траєкторією. Рух снаряда відбувається тільки тоді, коли на траєкторії прикладена одна сила, після чого єдине перешкода - від сили тяжіння. У попередньому атомі ми обговорювали, що таке різні компоненти об'єкта в русі снаряда. У цьому атомі ми обговоримо основні рівняння, які йдуть разом з ними в особливому випадку, в якому початкові позиції снаряда є нульовими (тобто\(\mathrm{x_0=0}\) і\(\mathrm{y_0=0}\)).

    Початкова швидкість

    Початкова швидкість може бути виражена у вигляді x компонентів і y складових:

    \[\begin{align} \mathrm{u_x} & \mathrm{=u⋅ \cos θ} \\ \mathrm{u_y} & \mathrm{=u⋅ \sin θ} \end{align}\]

    У цьому рівнянні\(\mathrm{u}\) позначає початкову величину швидкості і\(θ\) відноситься до кута снаряда.

    Час польоту

    Час польоту руху снаряда - це час від моменту, коли об'єкт проектується до моменту його досягнення на поверхню. Як ми обговорювали раніше,\(\mathrm{T}\) залежить від початкової величини швидкості і кута нахилу снаряда:

    \[\begin{align} \mathrm{T} & \mathrm{=\dfrac{2⋅u_y}{g} } \\ \mathrm{T} & \mathrm{=\dfrac{2⋅u⋅\sin ⁡θ}{g}} \end{align}\]

    Прискорення

    При русі снаряда немає прискорення в горизонтальному напрямку. Прискорення у вертикальному напрямку відбувається якраз завдяки гравітації, також відомому як вільне падіння:\(\mathrm{a}\)

    \[\begin{align} \mathrm{a_x} & \mathrm{=0} \\ \mathrm{a_y} &\mathrm{=−g} \end{align}\]

    Швидкість

    Горизонтальна швидкість залишається постійною, але вертикальна швидкість змінюється лінійно, тому що прискорення постійне. У будь-який момент\(\mathrm{t}\), швидкість становить:

    \[\begin{align} \mathrm{u_x} & \mathrm{=u⋅ \cos θ} \\ \mathrm{u_y} & \mathrm{=u⋅ \sin θ−g⋅t} \end{align}\]

    Ви також можете використовувати теорему Піфагора, щоб знайти швидкість:

    \[\mathrm{u=\sqrt{u_x^2+u_y^2}}\]

    Водотоннажність

    За часом, t, складовими зміщення є:

    \[\begin{align} \mathrm{x} & \mathrm{=u⋅t⋅ \cos ⁡θ} \\ \mathrm{y} & \mathrm{=u⋅t⋅ \sin ⁡θ−\dfrac{1}{2}gt^2} \end{align}\]

    Рівняння величини зсуву дорівнює\(\mathrm{Δr=\sqrt{x^2+y^2}}\).

    Параболічна траєкторія

    Ми можемо використовувати рівняння переміщення в напрямку x і y для отримання рівняння для параболічної форми руху снаряда:

    \[\mathrm{y=\tan θ⋅x−\dfrac{g}{2⋅u^2⋅ \cos ^2 θ}⋅x^2}\]

    Максимальна висота

    Максимальна висота досягається при\(\mathrm{v_y=0}\). Використовуючи це, ми можемо переставити рівняння швидкості, щоб знайти час, який знадобиться об'єкту, щоб досягти максимальної висоти.

    \[\mathrm{t_h=\dfrac{u⋅\sin θ}{g}}\]

    де\(\mathrm{t_h}\) стоїть час, необхідний для досягнення максимальної висоти. З рівняння переміщення ми можемо знайти максимальну висоту

    \[\mathrm{h=\dfrac{u^2⋅ \sin ^2 ⁡θ}{2⋅g}}\]

    Діапазон

    Діапазон руху фіксується умовою\(\mathrm{y=0}\). Використовуючи це, ми можемо переставити рівняння параболічного руху, щоб знайти діапазон руху:

    \[\mathrm{R=\dfrac{u^2⋅ \sin ⁡2 θ}{g}.}\]

    зображення

    Діапазон траєкторії: Діапазон траєкторії показаний на цьому малюнку.

    Снаряди під кутом: Це відео дає чітке і просте пояснення того, як вирішити проблему на снарядах, запущених під кутом. Я намагаюся пройти крок за кроком через цю складну проблему, щоб розкласти, як вирішити її надзвичайно чітким способом. 2D кінематичні проблеми потребують часу, щоб вирішити, робити нотатки про порядок того, як я її вирішив. З найкращими побажаннями. Налаштуйтеся на мої інші відео для отримання додаткової допомоги. Мир.

    Рішення проблем

    При русі снаряда об'єкт рухається параболічним шляхом; шлях, яким слідує об'єкт, називається його траєкторією.

    цілі навчання

    • Визначте, які компоненти мають важливе значення при визначенні руху снаряда об'єкта

    Раніше ми обговорювали рух снаряда та його ключові складові та основні рівняння. Використовуючи цю інформацію, ми можемо вирішити багато проблем, пов'язаних з рухом снаряда. Перш ніж ми це зробимо, давайте розглянемо деякі ключові фактори, які підуть у вирішення цієї проблеми.

    Що таке рух снаряда?

    Рух снаряда - це коли об'єкт рухається в двосторонньому симетричному параболічному шляху. Шляхом, яким слідує об'єкт, називається його траєкторією. Рух снаряда відбувається лише тоді, коли на початку прикладається одна сила, після чого єдиний вплив на траєкторію - це сила тяжіння.

    Які ключові компоненти руху снарядів?

    Ключовими компонентами, які нам потрібно запам'ятати, щоб вирішити проблеми руху снарядів, є:

    • Початковий кут запуску,\(\mathrm{θ}\)
    • Початкова швидкість,\(\mathrm{u}\)
    • Час польоту,\(\mathrm{T}\)
    • Прискорення,\(\mathrm{a}\)
    • Горизонтальна швидкість,\(\mathrm{v_x}\)
    • Вертикальна швидкість,\(\mathrm{v_y}\)
    • Водотоннажність,\(\mathrm{d}\)
    • Максимальна висота,\(\mathrm{H}\)
    • Діапазон,\(\mathrm{R}\)

    Як вирішити будь-яку проблему руху снаряда (метод Toolbox): Представляємо метод «Toolbox» для вирішення проблем руху снарядів! Тут ми використовуємо кінематичні рівняння та модифікуємо з початковими умовами для створення «інструментарію» рівнянь, за допомогою яких можна розв'язати класичну тричастинну задачу руху снаряда.

    Тепер розглянемо два приклади проблем, пов'язаних з рухом снаряда.

    Приклад\(\PageIndex{1}\):

    Приклад 1

    Припустимо, вам дано об'єкт, якому потрібно очистити два стовпчики однакової висоти, розділені певною відстанню. Зверніться до цього прикладу. Снаряд кидається\(\mathrm{25 \sqrt{2}}\) зі швидкістю м/с під кутом 45°. Якщо об'єкт повинен очистити обидва стовпи, кожен висотою 30 м, знайдіть мінімальне: (а) положення запуску на землі по відношенню до стовпів і (б) поділ між стовпами. Для простоти використовуйте постійну гравітації 10. Завдання будь-якого типу в фізиці набагато простіше вирішувати, якщо перераховувати речі, які ви знаєте («дані»).

    зображення

    Діаграма для прикладу 1: Використовуйте цю цифру як посилання для вирішення прикладу 1. Проблема полягає в тому, щоб переконатися, що об'єкт здатний очистити обидва пости.

    Рішення: Перше, що нам потрібно зробити, це з'ясувати, в який час tt об'єкт досягає зазначеної висоти. Оскільки рух знаходиться в параболічній формі, це буде відбуватися двічі: один раз при русі вгору, і знову, коли об'єкт рухається вниз. Для цього ми можемо використовувати рівняння зміщення у вертикальному напрямку\(\mathrm{y−y_0}\) :

    \[\mathrm{y−y_0=(v_y⋅t)−(\dfrac{1}{2}⋅g⋅t^2)}\]

    Підставляємо у відповідні змінні:

    \[\mathrm{v_y=u⋅ \sin θ=25 \sqrt{2} \dfrac{m}{s}⋅ \sin 45^{\circ}=25 \dfrac{m}{s}}\]

    Тому:

    \[\mathrm{30m=25⋅t−\dfrac{1}{2}⋅10⋅t^2}\]

    Ми можемо використовувати квадратне рівняння, щоб знайти, що корінням цього рівняння є 2s і 3s. Це означає, що снаряд досягне 30 м через 2 с, на шляху вгору, і через 3 с, на шляху вниз.

    Приклад 2

    Об'єкт запускається з підстави ухилу, який знаходиться під кутом 30°. Якщо кут запуску становить 60° від горизонталі, а швидкість запуску 10 м/с, який загальний час польоту? Наводиться наступна інформація:\(\mathrm{u=10 \frac{m}{s}; θ=60°; g=10 \frac{m}{s^2}}\).

    зображення

    Діаграма для прикладу 2: Коли ми маємо справу з об'єктом у русі снаряда на нахилі, нам спочатку потрібно використати задану інформацію для переорієнтації системи координат, щоб об'єкт запускався та впав на ту саму поверхню.

    Рішення: Для того, щоб врахувати кут нахилу, ми повинні переорієнтувати систему координат так, щоб точки проекції та повернення знаходилися на одному рівні. Кут проекції щодо\(\mathrm{x}\) напрямку дорівнює\(\mathrm{θ−α}\), а прискорення в\(\mathrm{y}\) напрямку -\(\mathrm{g⋅ \cos ⁡α}\). \(\mathrm{θ}\)Замінюємо на\(\mathrm{θ−α}\) і\(\mathrm{g}\) з\(\mathrm{g⋅ \cos ⁡α}\):

    \[\begin{align} \mathrm{T \; } & \mathrm{=\dfrac{2⋅u⋅ \sin (θ)}{g} = \dfrac{2⋅u⋅\sin (θ−α)}{g⋅ \cos (α)}=\dfrac{2⋅10⋅ \sin (60−30)}{10⋅\cos (30)} =\dfrac{20⋅ \sin (30)}{10⋅ \cos (30)} } \\ \mathrm{T \;} &\mathrm{=\dfrac{2}{\sqrt{3}}s} \end{align}\]

    Нульовий кут запуску

    Об'єкт, запущений горизонтально на висоті,\(\mathrm{H}\) подорожує по дальності\(\mathrm{v_0\sqrt{\frac{2H}{g}}}\) під час польоту\(\mathrm{T=\sqrt{\frac{2H}{g}}}\).

    цілі навчання

    • Поясніть взаємозв'язок між дальністю і часом польоту

    Рух снаряда - це форма руху, коли об'єкт рухається параболічним шляхом. Шляхом, яким слідує об'єкт, називається його траєкторією. Рух снаряда відбувається при прикладанні сили на початку траєкторії для запуску (після цього снаряд піддається тільки гравітації).

    Однією з ключових складових руху снаряда, і траєкторії, за якою він слідує, є початковий кут запуску. Кут, під яким запускається об'єкт, диктує дальність, висоту та час польоту, який буде відчувати об'єкт під час руху снаряда. показує різні шляхи для одного і того ж об'єкта, що запускається з однаковою початковою швидкістю та різними кутами запуску. Як показано на малюнку, чим більше початковий кут запуску і максимальна висота, тим більше час польоту об'єкта.

    зображення

    Траєкторії снарядів: Кут запуску визначає дальність і максимальну висоту, яку буде відчувати об'єкт після запуску. Це зображення показує, що шлях одного і того ж об'єкта запускається з однаковою швидкістю, але різними кутами.

    Раніше ми обговорювали вплив різних кутів запуску на дальність, висоту та час польоту. Однак що буде, якщо немає кута, а об'єкт просто запущений горизонтально? Має сенс, що об'єкт повинен бути запущений на певній висоті (\(\mathrm{H}\)), інакше він не проїхав би дуже далеко, перш ніж вдаритися об землю. Розберемо, як\(\mathrm{H}\) рухається об'єкт, запущений горизонтально на висоті. У нашому випадку це коли\(\mathrm{α}\) дорівнює 0.

    зображення

    Рух снаряда: Снаряд рухається слідом за parabola.Initial кут запуску αα, а швидкість є\(\mathrm{v_0}\).

    Тривалість польоту

    У початковій швидкості (\(\mathrm{v_0}\)) немає вертикальної складової, оскільки об'єкт запускається горизонтально. Оскільки об'єкт проходить відстань\(\mathrm{H}\) у вертикальному напрямку до того, як він вдариться про землю, ми можемо використовувати кінематичне рівняння для вертикального руху:

    \[\mathrm{(y−y_0)=−H=0⋅T−\dfrac{1}{2}gT^2}\]

    Тут\(\mathrm{T}\) вказується тривалість польоту перед тим, як об'єкт потрапляє на землю. Тому:

    \[\mathrm{T=\sqrt{\dfrac{2H}{g}}}\]

    Діапазон

    У горизонтальному напрямку об'єкт рухається з постійною швидкістю\(\mathrm{v_0}\) під час польоту. Тому діапазон\(\mathrm{R}\) (в горизонтальному напрямку) задається як:

    \[\mathrm{R=v_0⋅T=v_0\sqrt{\dfrac{2H}{g}}}\]

    Загальний кут запуску

    Початковий кут запуску (0-90 градусів) об'єкта в русі снаряда визначає дальність, висоту та час польоту цього об'єкта.

    цілі навчання

    • Виберіть відповідне рівняння, щоб знайти дальність, максимальну висоту та час польоту

    Рух снаряда - це форма руху, коли об'єкт рухається в двосторонньому симетричному параболічному шляху. Шляхом, яким слідує об'єкт, називається його траєкторією. Рух снаряда відбувається тільки тоді, коли на початку траєкторії прикладена одна сила, після чого єдине втручання - від сили тяжіння.

    Однією з ключових складових руху снаряда і траєкторії, за якою він слідує, є початковий кут запуску. Цей кут може бути в будь-якому місці від 0 до 90 градусів. Кут, під яким запускається об'єкт, диктує дальність, висоту та час польоту, який він буде відчувати під час руху снаряда. показує різні шляхи для одного і того ж об'єкта, запущеного з однаковою початковою швидкістю під різними кутами запуску. Як видно з малюнка, чим більше початковий кут запуску, тим ближче об'єкт підходить до максимальної висоти і тим більше час польоту. Найбільший діапазон буде відчуватися при куті запуску до 45 градусів.

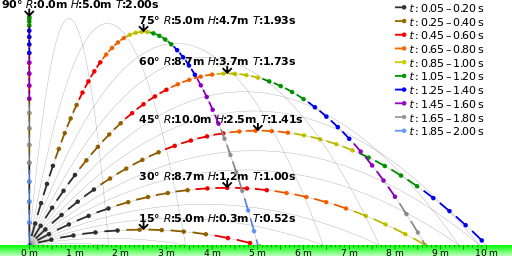
    зображення

    Кут запуску: Кут запуску визначає дальність і максимальну висоту, яку буде відчувати об'єкт після запуску. Це зображення показує, що шлях одного і того ж об'єкта запускається з однаковою швидкістю, але різними кутами.

    Дальність, максимальну висоту і час польоту можна знайти, якщо знати початковий кут запуску і швидкість, використовуючи наступні рівняння:

    \[\begin{align} \mathrm{R \;} & \mathrm{=\dfrac{v_i^2 \sin ^⁡2 θ_i}{g}} \\ \mathrm{h \;} & \mathrm{=\dfrac{v_i^2 \sin ^2 ⁡θ_i}{2g}} \\ \mathrm{T \;} & \mathrm{=\dfrac{2v_i \sin θ}{g}} \end{align}\]

    Де R — дальність, h — максимальна висота, T — час польоту, v i — початкова швидкість, θ i — початковий кут запуску, g — гравітація.

    Тепер, коли ми розуміємо, як кут запуску відіграє важливу роль у багатьох інших компонентах траєкторії руху об'єкта в русі снаряда, ми можемо застосувати ці знання для того, щоб зробити об'єкт приземлитися там, де ми цього хочемо. Якщо є певна відстань, d, що ви хочете, щоб ваш об'єкт пішов, і ви знаєте початкову швидкість, з якою він буде запущений, початковий кут запуску, необхідний для того, щоб отримати це відстань називається кутом досяжності. Його можна знайти за допомогою наступного рівняння:

    \[\mathrm{θ=\dfrac{1}{2} \sin ^{−1}(\dfrac{gd}{v^2})}\]

    Ключові моменти: Діапазон, Симетрія, Максимальна висота

    Рух снаряда - це форма руху, де об'єкт рухається параболічним шляхом. Шляхом, яким слідує об'єкт, називається його траєкторією.

    цілі навчання

    • Побудувати модель руху снаряда, включаючи час польоту, максимальну висоту і дальність

    Що таке рух снаряда?

    Рух снаряда - це форма руху, коли об'єкт рухається в двосторонньому симетричному параболічному шляху. Шляхом, яким слідує об'єкт, називається його траєкторією. Рух снаряда відбувається тільки тоді, коли на траєкторії прикладена одна сила, після чого єдине перешкода - від сили тяжіння. У цьому атомі ми обговоримо, що таке різні компоненти об'єкта в русі снаряда, ми обговоримо основні рівняння, які йдуть разом з ними в іншому атомі, «Основні рівняння та параболічний шлях»

    Основні компоненти руху снаряда:

    Час польоту, Т:

    Час польоту руху снаряда - це саме те, як він звучить. Це час від того, коли об'єкт проектується до моменту його досягнення на поверхню. Час польоту залежить від початкової швидкості об'єкта і кута проекції, θ. Коли точка проекції і точка повернення знаходяться на одній горизонтальній площині, чисте вертикальне зміщення об'єкта дорівнює нулю.

    Симетрія:

    Весь рух снаряда відбувається в двосторонньому симетричному шляху, до тих пір, поки точки проекції і повернення відбуваються уздовж однієї і тієї ж горизонтальної поверхні. Двостороння симетрія означає, що рух симетричне у вертикальній площині. Якби ви намалювали пряму вертикальну лінію з максимальної висоти траєкторії, вона б дзеркала себе уздовж цієї лінії.

    Максимальна висота, H:

    Максимальна висота об'єкта в траєкторії снаряда виникає, коли вертикальна складова швидкості, виви, дорівнює нулю. У міру руху снаряда вгору він йде проти сили тяжіння, і тому швидкість починає сповільнюватися. В кінцевому підсумку вертикальна швидкість досягне нуля, а снаряд розганяється вниз під дією сили тяжіння відразу. Як тільки снаряд досягає максимальної висоти, він починає прискорюватися вниз. Це також точка, де ви б намалювали вертикальну лінію симетрії.

    Дальність дії снаряда, R:

    Дальність дії снаряда - це зміщення в горизонтальному напрямку. У цьому напрямку немає прискорення, оскільки гравітація діє лише вертикально. показує лінію діапазону. Як і час польоту і максимальна висота, дальність снаряда є функцією початкової швидкості.

    зображення

    Дальність: Дальність руху снаряда, як видно на цьому зображенні, не залежить від сил тяжіння.

    Ключові моменти

    • Об'єкти, які проектуються з, і приземляються на одній горизонтальній поверхні, матимуть вертикально симетричну траєкторію.
    • Час, який потрібно від об'єкта, який потрібно проектувати і приземлитися, називається часом польоту. Це залежить від початкової швидкості снаряда і кута проекції.
    • Коли снаряд досягне вертикальної швидкості нуля, це максимальна висота снаряда і тоді гравітація візьме на себе і прискорить об'єкт вниз.
    • Горизонтальне зміщення снаряда називається дальністю дії снаряда, і залежить від початкової швидкості руху об'єкта.
    • При вирішенні завдань, пов'язаних з рухом снаряда, ми повинні пам'ятати всі ключові складові руху і основні рівняння, які йдуть разом з ними.
    • Використовуючи цю інформацію, ми можемо вирішувати багато різних типів задач, якщо ми можемо проаналізувати інформацію, яку нам дають, і використовувати основні рівняння для її з'ясування.
    • Щоб очистити дві стійки однакової висоти та з'ясувати, яка відстань між цими стовпами, нам потрібно пам'ятати, що траєкторія є параболічною формою і що існує два різних часу, коли об'єкт досягне висоти стовпів.
    • Маючи справу з об'єктом в русі снаряда на нахилі, нам спочатку потрібно використовувати задану інформацію для переорієнтації системи координат, щоб об'єкт був запущений і впав на одну поверхню.
    • Для нульового кута запуску в початковій швидкості немає вертикальної складової.
    • Тривалість польоту до того, як об'єкт потрапить на землю, задається як\(\mathrm{T=\sqrt{\frac{2H}{g}}}\).
    • У горизонтальному напрямку об'єкт рухається з постійною швидкістю v 0 під час польоту. Діапазон R (в горизонтальному напрямку) задається як:\(\mathrm{R=v_0⋅T=v_0\sqrt{\dfrac{2H}{g}}}\).
    • Якщо той же об'єкт запущений з однаковою початковою швидкістю, висота і час польоту збільшаться пропорційно початковому куту запуску.
    • Об'єкт, запущений в рух снаряда, матиме початковий кут запуску в будь-якому місці від 0 до 90 градусів.
    • Дальність дії об'єкта, враховуючи початковий кут запуску та початкову швидкість, знайдено за допомогою:\(\mathrm{R=\dfrac{v_i^2 \sin ^⁡2 θ_i}{g}}\).
    • Максимальна висота об'єкта, враховуючи початковий кут запуску та початкову швидкість, знайдено при:\(\mathrm{ｈ=\dfrac{v_i^2 \sin ^2 ⁡θ_i}{2g}}\).
    • Час польоту об'єкта, враховуючи початковий кут запуску та початкову швидкість, знайдено з:\(\mathrm{T=\dfrac{2v_i \sin θ}{g}}\).
    • Кут досяжності - це кут, під яким повинен бути запущений об'єкт, щоб досягти певної відстані:\(\mathrm{θ=\dfrac{1}{2} \sin ^{−1}(\dfrac{gd}{v^2})}\).
    • Об'єкти, які проектуються і приземляються на одній горизонтальній поверхні, матимуть шлях, симетричний щодо вертикальної лінії через точку на максимальній висоті снаряда.
    • Час, який потрібно від об'єкта, який потрібно проектувати і приземлитися, називається часом польоту. Вона залежить від початкової швидкості снаряда і кута проекції.
    • Максимальна висота снаряда - це коли снаряд досягає нульової вертикальної швидкості. З цієї точки вертикальна складова вектора швидкості буде спрямована вниз.
    • Горизонтальне зміщення снаряда називається дальністю дії снаряда і залежить від початкової швидкості руху об'єкта.
    • Якщо об'єкт проектується з однаковою початковою швидкістю, але двома взаємодоповнюючими кутами проекції, дальність дії снаряда буде однаковою.

    Ключові умови

    • траєкторія: шлях тіла, коли воно рухається через простір.
    • симетричні: Виявлення симетрії; мають гармонійне або пропорційне розташування частин; мають відповідні частини або відносини.
    • переорієнтуватися: орієнтуватися заново; змусити зіткнутися з іншим напрямком
    • Гравітація: результуюча сила на поверхні Землі, тяжіння земними масами та відцентрова псевдосила, спричинена обертанням Землі.
    • двостороння симетрія: властивість бути симетричною щодо вертикальної площини

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ