Skip to main content
LibreTexts - Ukrayinska

27.3: Релятивістські величини

  1. Last updated
  2. Save as PDF
  • Page ID
    75130

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Експрес-формули швидкості-додавання для об'єктів на швидкостях значно менших і наближаються до швидкості світла

    Формула швидкості-додавання - це рівняння, яке пов'язує швидкості рухомих об'єктів в різних системах відліку.

    Як спостерігав Галілео Галілей у 17 столітті, якщо корабель рухається відносно берега зі швидкістю vv, а муха рухається зі швидкістю uu, як вимірюється на кораблі, обчислення швидкості мухи, виміряної на березі, - це те, що мається на увазі додавання швидкостей vv і uu. Коли і муха, і корабель рухаються повільно порівняно зі швидкістю світла, досить точно використовувати векторну суму s=u+vs=u+v, де ss - швидкість польоту відносно берега.

    Відповідно до теорії особливої відносності, кадр корабля має різну тактову частоту і міру відстані, а поняття одночасності в напрямку руху змінюється, тому закон додавання для швидкостей змінюється.

    Оскільки особлива відносність диктує, що швидкість світла однакова у всіх рамках відліку, світло, що сяяв спереду автомобіля, що рухається, не може йти швидше, ніж світло від стаціонарного ліхтаря. Оскільки це суперечить тому, що Галілей використовував для додавання швидкостей, повинен бути новий закон додавання швидкості.

    Ця зміна не помітна при низьких швидкостях, але зі збільшенням швидкості до швидкості світла це стає важливим. Закон додавання також називають законом складу для швидкостей. Для колінеарних рухів швидкість мухи щодо берега задається наступним рівнянням:

    \[\mathrm { s } = \frac { \mathrm { v } + \mathrm { u } } { 1 + \mathrm { vu } / \mathrm { c } ^ { 2 } }\]

    Закон композиції для швидкостей дав перший тест кінематики спеціальної теорії відносності. Використовуючи інтерферометр Майкельсона, Гіпполіт Фізо вимірював швидкість світла в рідині, що рухається паралельно світлу в 1851 році. Швидкість світла в рідині повільніше, ніж швидкість світла у вакуумі, і вона змінюється, якщо рідина рухається разом зі світлом. Швидкість світла в колінеарній рухомій рідині точно прогнозується колінеарним випадком релятивістської формули.

    зображення

    Налаштування експерименту Fizeau: світловий промінь, що виходить від джерела S', відбивається променевим розгалужувачем G і колімується в паралельний промінь лінзою L. Після проходження щілин O1 і O2 два промені світла рухаються по трубках A1 і A2, через які вода тече вперед і назад, як показані стрілками. Промені відбиваються від дзеркала m у фокусі лінзи L', так що один промінь завжди поширюється в тому ж напрямку, що і водний потік, а інший промінь протилежний напрямку потоку води. Після проходження вперед і назад через трубки обидва промені об'єднуються в S, де вони виробляють інтерференційні бахроми, які можна візуалізувати через ілюстрований окуляр. Інтерференційну картину можна проаналізувати для визначення швидкості світла, що рухається уздовж кожної ніжки трубки.

    Релятивістський імпульс

    Релятивістський імпульс\(\mathrm { m_0 }\) задається як\(\gamma \mathrm { m } _ { 0 } \mathrm { v }\) де знаходиться інваріантна маса об'єкта і\(\gamma\) перетворення Лоренца.

    навчальні цілі

    • Порівняйте ньютонівські і релятивістські моменти для об'єктів зі швидкостями набагато менше і наближаються до швидкості світла.

    Релятивістський імпульс

    Ньютонівська фізика передбачає, що абсолютний час і простір існують поза будь-якого спостерігача. Це породжує галілейську відносність, яка стверджує, що закони руху однакові у всіх інерційних рамках. Це також призводить до прогнозування того, що швидкість світла може змінюватися від одного еталонного кадру до іншого. Однак це суперечить спостереженню. У теорії особливої відносності Альберт Ейнштейн зберігає постулат про те, що рівняння руху не залежать від системи відліку, а передбачає, що швидкість світла c є інваріантною. Як результат, позиція і час у двох опорних кадрах пов'язані перетворенням Лоренца замість перетворення Галілея.

    зображення

    Альберт Ейнштейн: Альберт Ейнштейн у 1921 році

    Розглянемо, наприклад, опорний кадр, що рухається відносно іншого зі швидкістю v в напрямку x. Перетворення Галілея дає координати рухомого кадру як

    \[\mathrm { t } ^ { \prime } = \mathrm { t }\]

    \[\mathrm { x } ^ { \prime } = \mathrm { x } - \mathrm { v } \mathrm{ t } \]

    в той час як перетворення Лоренца дає

    \[\mathrm{t ^ { \prime } = \gamma \left( t - \dfrac { v x } { c ^ { 2 } } \right)}\]

    \[\mathrm { x } ^ { \prime } = \gamma ( \mathrm { x } - \mathrm { v t} )\]

    де\(γ\) знаходиться фактор Лоренца:

    \[\gamma = \dfrac { 1 } { \sqrt { 1 - ( \mathrm { v } / \mathrm { c } ) ^ { 2 } } }\]

    Закони збереження у фізиці, такі як закон збереження імпульсу, повинні бути інваріантними. Тобто майно, яке необхідно зберегти, має залишатися незмінним незалежно від зміни умов вимірювання. Це означає, що закон про збереження повинен триматися в будь-якій системі відліку. Другий закон Ньютона [з масою, зафіксованою у виразі для імпульсу (p=m* v)], не є інваріантним при перетворенні Лоренца. Однак його можна зробити інваріантним, зробивши інерційну масу m об'єкта функцією швидкості:

    \[\mathrm { m } = \gamma \mathrm { m } _ { 0 }\]

    де\(\mathrm { m } _ { 0 }\) - інваріантна маса об'єкта.

    Змінений імпульс,

    \[\mathrm { p } = \gamma \mathrm { m } _ { 0 } \mathrm { v }\]

    підкоряється другому закону Ньютона:

    \[\mathrm { F } = \dfrac { \mathrm { d } \mathrm { p } } { \mathrm { d } t }\]

    Важливо відзначити, що для швидкостей, значно менших швидкості світла, ньютонівський імпульс і релятивістський імпульс приблизно однакові. Однак, коли хтось наближається до швидкості світла, релятивістський імпульс стає нескінченним, тоді як імпульс Ньютона продовжує лінійно зростати. Таким чином, необхідно використовувати вираз для релятивістського імпульсу, коли людина має справу зі швидкістю поблизу швидкості світла.

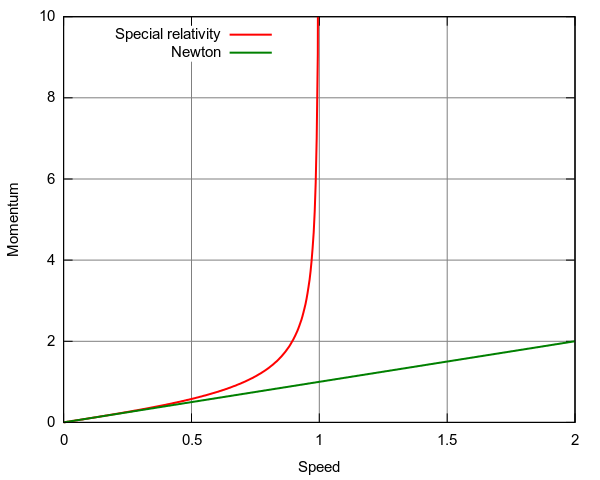
    зображення

    Релятивістський та ньютонівський імпульс: Ця цифра ілюструє, що релятивістський імпульс наближається до нескінченності при наближенні швидкості світла. Ньютонівський імпульс зростає лінійно зі швидкістю.

    Релятивістська енергія і маса

    У спеціальній теорії відносності, коли об'єкт наближається до швидкості світла, енергія та імпульс об'єкта збільшуються без обмежень.

    навчальні цілі

    • Оцініть можливість руху об'єкта зі швидкістю світла

    Релятивістська енергія і маса

    У спеціальній теорії відносності об'єкт, який має масу, не може подорожувати зі швидкістю світла. Коли об'єкт наближається до швидкості світла, енергія та імпульс об'єкта збільшуються без обмежень. Релятивістські поправки на енергію і масу потрібно робити через те, що швидкість світла у вакуумі постійна у всіх еталонних кадрах. Збереження маси і енергії - добре прийняті закони фізики. Для того щоб ці закони тримали у всіх довідкових рамках, повинна застосовуватися спеціальна відносність. Важливо відзначити, що для об'єктів зі швидкостями, які значно нижче швидкості світла, що вирази для релятивістської енергії і маси виходять значення, які приблизно рівні їх ньютонівським аналогам.

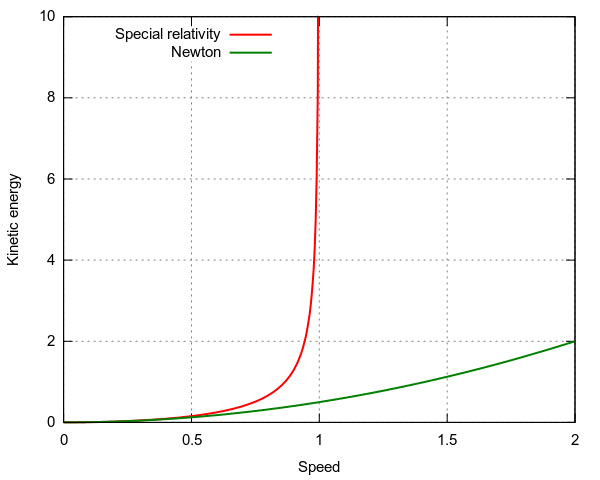
    зображення

    Релятивістська та ньютонівська кінетична енергія: Ця цифра ілюструє, як релятивістська та ньютонівська кінетична енергія пов'язані зі швидкістю об'єкта. Релятивістська кінетична енергія збільшується до нескінченності, коли об'єкт наближається до швидкості світла, це свідчить про те, що жодне тіло з масою не може досягти швидкості світла. З іншого боку, кінетична енергія Ньютона продовжує збільшуватися без обмежень у міру збільшення швидкості об'єкта.

    Релятивістська маса

    Релятивістська маса була визначена Річардом Толманом, зображеним зліва від Альберта Ейнштейна тут в 1934 році, як який утримує для всіх частинок, включаючи ті, що рухаються зі швидкістю світла. Для більш повільної, ніж світла частинки, частинки з ненульовою масою спокою, формула стає там, де знаходиться маса решти і є коефіцієнтом Лоренца. Коефіцієнт Лоренца дорівнює:\(\gamma = \frac { 1 } { \sqrt { 1 - \mathrm { v } ^ { 2 } / c ^ { 2 } } }\), де v - відносна швидкість між інерційними рамками відліку, а c - швидкість світла.

    зображення

    Річард Толман і Альберт Ейнштейн: Річард Толман (1881 — 1948) з Альбертом Ейнштейном (1879 — 1955) в Каліфорнійському технічному техніці, 1932

    Коли відносна швидкість дорівнює нулю, просто дорівнює 1, а релятивістська маса зменшується до маси спокою. Зі збільшенням швидкості до швидкості світла (c) знаменник правого боку наближається до нуля, а отже, наближається до нескінченності.

    У формулі імпульсу маса, що виникає, - це релятивістська маса. Іншими словами, релятивістська маса - це постійна пропорційності між швидкістю і імпульсом.

    Хоча другий закон Ньютона залишається дійсним у формі, похідна форма не є дійсною, оскільки in, як правило, не є постійною.

    Релятивістська енергія

    Релятивістська енергія (\(\mathrm { E } _ { \mathrm { r } } = \sqrt { \left( \mathrm { m } _ { 0 } \mathrm { c } ^ { 2 } \right) ^ { 2 } + ( \mathrm { pc } ) ^ { 2 } }\)) пов'язана з масою спокою за допомогою наступного рівняння:\(m = \frac { \sqrt { ( E ^ { 2 } - ( p c ) ^ { 2 } } } { c ^ { 2 } }\). Тут термін являє собою квадрат евклідової норми (загальної довжини вектора) різних векторів імпульсу в системі, який зводиться до квадрата величини простого імпульсу, якщо розглядати лише одну частинку. Це рівняння зводиться до того, коли термін імпульсу дорівнює нулю. Для фотонів, де рівняння зводиться до.

    Сьогодні прогнози релятивістської енергії та маси регулярно підтверджуються експериментальними даними прискорювачів частинок, таких як релятивістський важкий іонний коллайдер. Збільшення релятивістського імпульсу та енергії не тільки точно вимірюється, але й необхідно для розуміння поведінки циклотронів та синхротронів, які прискорюють частинки до близької швидкості світла.

    Матерія і антиречовина

    Антиречовина складається з античастинок, які мають таку ж масу, як частинки звичайної речовини, але протилежний заряд і квантовий спін.

    навчальні цілі

    • Опишіть властивості античастинок

    Антиречовина - це матеріал, що складається з античастинок, які мають таку ж масу, як частинки звичайної речовини, але мають протилежний заряд і квантовий спін. Античастинки зв'язуються між собою, утворюючи антиречовину так само, як звичайні частинки зв'язуються, утворюючи нормальну речовину. Наприклад, позитрон (античастинка електрона, з символом е +) і антипротон (символ р —) можуть утворювати атом антиводню. Крім того, змішування речовини та антиречовини може призвести до знищення обох, так само, як це робить змішування античастинок і частинок. Це породжує високоенергетичні фотони (гамма-промені) та інші пари частинок - античастинки. Кінцевим результатом зустрічі антиречовини речовини є виділення енергії, пропорційної масі, як показано в рівнянні еквівалентності маси і енергії, E = mc 2.

    зображення

    Атоми антиводню та водню: Антиводень складається з антипротона та позитрона; водень складається з протона та електрона.

    Майже вся матерія, яку можна спостерігати з землі, здається, зроблена з матерії, а не з антиречовини. Якби існували області простору, де переважають антиречовини, гамма-промені, що утворюються в реакціях анігіляції вздовж кордону між речовиною та антиречовиною областей, були б виявлені.

    Антиречовина все ще може існувати у відносно великих кількостях у далеких галактиках через космічну інфляцію в первісний час Всесвіту. Очікується, що антиречовинні галактики, якщо вони існують, матимуть ті ж хімічні та поглинання та спектри випромінювання, що й галактики з нормальною речовиною, і їх астрономічні об'єкти будуть спостережно ідентичними, що ускладнює їх відрізнення від галактик з нормальною речовиною.

    Існує значні припущення щодо того, чому спостережуваний Всесвіт, мабуть, складається майже повністю з матерії (на відміну від суміші речовини та антиречовини), чи існують інші місця, які майже повністю складаються з антиречовини, і які технології можуть бути можливі, якщо антиречовину можна було запрягати. В цей час очевидна асиметрія матерії і антиречовини у видимому Всесвіті є однією з найбільших невирішених проблем фізики.

    Релятивістська кінетична енергія

    Релятивістська кінетична енергія може бути виражена так:\(\mathrm { E } _ { \mathrm { k } } = \frac { \mathrm { mc } ^ { 2 } } { \sqrt { 1 - ( \mathrm { v } / \mathrm { c } ) ^ { 2 } ) } } - \mathrm { mc } ^ { 2 }\) де мм\(\mathrm{v}\) - маса спокою,\(\mathrm{c}\) це швидкість, швидкість світла.

    навчальні цілі

    • Порівняйте класичну і релятивістську кінетичні енергії для об'єктів зі швидкостями набагато менше і наближаються до швидкості світла.

    У класичній механіці кінетична енергія об'єкта залежить від маси тіла, а також від його швидкості. Кінетична енергія дорівнює масі, помноженої на квадрат швидкості, помноженої на постійну 1/2. Рівняння дається у вигляді:

    \[\mathrm { E } _ { \mathrm { k } } = \dfrac { 1 } { 2 } \mathrm { m } \mathrm { v } ^ { 2 }\]

    де мм - маса, а vv - швидкість (або швидкість) тіла.

    Класична кінетична енергія об'єкта пов'язана з його імпульсом рівнянням:

    \[\mathrm { E } _ { \mathrm { k } } = \dfrac { \mathrm { p } ^ { 2 } } { 2 \mathrm { m } }\]

    де pp - імпульс.

    Якщо швидкість тіла становить значну частку швидкості світла, необхідно використовувати спеціальну відносність для обчислення його кінетичної енергії. Важливо знати, як застосовувати особливу відносність до проблем з високошвидкісними частинками. У спеціальній теорії відносності ми повинні змінити вираз для лінійного імпульсу. Використовуючи мм для маси спокою,\(\mathrm{v}\) а також\(\mathcal { V }\) для швидкості і швидкості об'єкта відповідно, і cc для швидкості світла у вакуумі, релятивістський вираз для лінійного імпульсу:

    зображення

    Журнал Time - 1 липня 1946 року: Популярний зв'язок між Ейнштейном та атомною бомбою був помітним на обкладинці журналу Time (липень 1946) написанням рівняння на самому грибному хмарі.\(\mathrm{E = mc^2}\)

    \(\mathrm { p } = \mathrm { m } \gamma \mathrm { v }\), де\(γ\) знаходиться фактор Лоренца:

    \(\gamma = \dfrac { 1 } { \sqrt { 1 - ( \mathrm{ v } / \mathrm { c } ) ^ { 2 } } }\)

    Оскільки кінетична енергія об'єкта пов'язана з його імпульсом, ми інтуїтивно знаємо, що релятивістський вираз кінетичної енергії також буде відрізнятися від його класичного аналога. Дійсно, релятивістський вираз для кінетичної енергії є:

    \[\mathrm { E } _ { \mathrm { k } } = \dfrac { \mathrm { mc } ^ { 2 } } { \sqrt { 1 - ( \mathrm { v } / \mathrm { c } ) ^ { 2 } ) } } - \mathrm { mc } ^ { 2 }\]

    Рівняння показує, що енергія об'єкта наближається до нескінченності, коли швидкість vv наближається до швидкості світла cc. Таким чином неможливо розігнати об'єкт через цю межу.

    Математичним побічним продуктом цього розрахунку є формула масово-енергетичної еквівалентності (згадується в). Організм в стані спокою повинен володіти енергійністю, рівною:

    \[\mathrm { E } _ { \mathrm { rest } } = \mathrm { E } _ { 0 } = \mathrm { mc } ^ { 2 }\]

    Загальним виразом для кінетичної енергії об'єкта, який не знаходиться в стані спокою, є:

    \(\mathrm { KE } = \mathrm { mc } ^ { 2 } - \mathrm { m } _ { 0 } \mathrm { c } ^ { 2 }\), Де m - релятивістська маса об'єкта, а m 0 - маса спокою об'єкта.

    При низькій швидкості (v<<cv<<c) релятивістська кінетична енергія може бути добре наближена класичною кінетичною енергією. Ми можемо показати, що це правда, використовуючи розширення Тейлора для взаємного квадратного кореня і зберігаючи перші два члени рівняння релятивістської кінетичної енергії. Коли ми це робимо, ми отримуємо:

    \[\mathrm { E } _ { \mathrm { k } } \approx \mathrm { mc } ^ { 2 } \left( 1 + \frac { 1 } { 2 } \mathrm { v } ^ { 2 } / \mathrm { c } ^ { 2 } \right) - \mathrm { mc } ^ { 2 } = \dfrac { 1 } { 2 } \mathrm { mv } ^ { 2 }\]

    Таким чином, загальна енергія може бути розділена на енергію маси спокою плюс традиційна класична кінетична енергія на малих швидкостях.

    Ключові моменти

    • Коли два об'єкти рухаються повільно в порівнянні зі швидкістю світла, досить точно використовувати векторну суму швидкостей:\(\mathrm{s=u+v}\).
    • Зі збільшенням швидкості до швидкості світла векторна сума швидкостей замінюється на:\(\mathrm { s } = \frac { \mathrm { v } + \mathrm { u } } { 1 + \mathrm { vu } / \mathrm { c } ^ { 2 } }\).
    • Закон композиції для швидкостей дав перший тест кінематики спеціальної теорії відносності, коли за допомогою інтерферометра Майкельсона Гіпполіт Фізо вимірював швидкість світла в рідині, що рухається паралельно світлу.
    • Ньютонівська фізика передбачає, що абсолютний час і простір існують поза будь-яким спостерігачем, в результаті чого створюється прогноз, що швидкість світла може змінюватися від одного опорного кадру до іншого.
    • У теорії спеціальної відносності рівняння руху не залежать від системи відліку, тоді як швидкість світла (с) є інваріантною.
    • В області класичної механіки релятивістський імпульс тісно наближає ньютонівський імпульс. При низькій швидкості γm0vγm0v приблизно дорівнює m0vm0v, ньютонівському виразу для імпульсу.
    • У спеціальній теорії відносності об'єкт, який має масу, не може подорожувати зі швидкістю світла.
    • Релятивістська маса визначається як\(\mathrm { m } _ { \mathrm { rel } } = \frac { \mathrm { E } } { \mathrm { c } ^ { 2 } }\) і може розглядатися як постійна пропорційності між швидкістю і імпульсом.
    • Релятивістська енергія пов'язана з масою спокою за допомогою наступного рівняння:\(\mathrm { E } _ { \mathrm { r } } = \sqrt { \left( \mathrm { m } _ { 0 } \mathrm { c } ^ { 2 } \right) ^ { 2 } + ( \mathrm { pc } ) ^ { 2 } }\).
    • Кінцевим результатом зустрічі антиречовини речовини є виділення енергії, пропорційної масі, як показано в рівнянні еквівалентності маси і енергії,\(\mathrm{E = mc^2}\).
    • Хоча майже вся речовина, яку можна спостерігати з Землі, здається, зроблена з речовини, а не з антиречовини, антиречовина все ще може існувати у відносно великих кількостях у далеких галактиках.
    • Ніякого пояснення очевидної асиметрії речовини і антиречовини у видимому Всесвіті не існує.
    • Релятивістське рівняння кінетичної енергії показує, що енергія об'єкта наближається до нескінченності, коли швидкість наближається до швидкості світла. Таким чином неможливо розігнати об'єкт через цю межу.
    • Розрахунки кінетичної енергії призводять до формули еквівалентності маси -енергії:\(\mathrm { E } _ { \mathrm { rest } } = \mathrm { E } _ { 0 } = \mathrm { mc } ^ { 2 }\).
    • При низькій швидкості (\(\mathrm { v } < < \mathrm { C }\)) релятивістська кінетична енергія може бути наближена класичною кінетичною енергією. Таким чином, загальна енергія може бути розділена на енергію маси решти плюс традиційну ньютонівську кінетичну енергію на малих швидкостях.

    Ключові умови

    • спеціальна теорія відносності: теорія, яка (нехтуючи ефектами гравітації) узгоджує принцип відносності із спостереженням про те, що швидкість світла постійна у всіх системах відліку.
    • інтерферометр: будь-який з декількох приладів, які використовують інтерференцію хвиль для визначення довжин хвиль і швидкостей хвиль, визначення показників заломлення та вимірювання малих відстаней, температурних змін, напружень та багатьох інших корисних вимірювань.
    • швидкість світла: швидкість електромагнітного випромінювання в ідеальному вакуумі: рівно 299,792,458 метрів в секунду за визначенням
    • Перетворення Галілея: перетворення, яке використовується для перетворення між координатами двох опорних кадрів, які відрізняються лише постійним відносним рухом у конструкціях ньютонівської фізики.
    • Перетворення Лоренца: перетворення, що пов'язує просторово-часові координати одного кадру відліку до іншого в спеціальній теорії відносності
    • Коефіцієнт Лоренца: Коефіцієнт, який використовується в спеціальній теорії відносності, для обчислення ступеня розширення часу, скорочення довжини та релятивістської маси об'єкта, що рухається відносно спостерігача.
    • маса спокою: маса тіла, коли воно не рухається відносно спостерігача
    • анігіляція: процес частинки та відповідного античастинки об'єднання для отримання енергії
    • позитрон: еквівалент антиречовини електрона, що має таку ж масу, але позитивний заряд.
    • антиречовина: речовина, яка складається з античастинок тих, що складають нормальну речовину
    • класична механіка: Усі фізичні закони природи, які враховують поведінку нормального світу, але руйнуються при роботі з дуже малими (див. Квантова механіка) або дуже швидкими або дуже важкими (див. Відносність).

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ