Skip to main content
LibreTexts - Ukrayinska

27.4: Наслідки спеціальної відносності

  1. Last updated
  2. Save as PDF
  • Page ID
    75117

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Сформулювати основні зміни в розумінні часу, простору, маси та енергії, які були введені теорією спеціальної відносності

    Теорія спеціальної відносності та її наслідки стимулювали зміну парадигми в нашому розумінні природи Всесвіту, фундаментальною тканиною якої є простір і час. До 1905 року вчені розглядали простір і час як цілком самостійні об'єкти. Час не міг вплинути на простір, а простір не міг вплинути на час. Однак після 1905 року Спеціальна теорія відносності зруйнувала цей старий, але інтуїтивний погляд. Зокрема, Спеціальна відносність показала нам, що простір і час не незалежні один від одного, але можуть змішуватися один в одного і тому повинні розглядатися як один і той же об'єкт, який ми позначимо як простор-час. Наслідки змішування простору/часу:

    • розширення часу
    • і скорочення довжини.

    Інші важливі наслідки, про які піде мова в іншому розділі:

    • Відносність одночасності (для певних подій послідовність, в якій вони відбуваються, залежить від спостерігача)
    • Ніщо не може рухатися швидше швидкості світла (значення швидкості світла позначимо як куб)

    Чому відбувається змішування між простором і часом? Для того, щоб вивчити це, ми повинні знати основоположні принципи відносності. Ними є:

    1. Принцип відносності: Закони фізики для спостерігачів, які не прискорюються відносно один одного, повинні бути однаковими.
    2. Принцип інваріантної швидкості світла: Всі спостерігачі, рухаючись з постійною швидкістю, вимірюють однакову швидкість світла незалежно від того, наскільки швидко вони рухаються.

    Якщо прийняти другий принцип як факт, то відразу випливає, що простір і час не є незалежними. Чому? Давайте розглянемо експеримент, в якому є джерело світла, нерухомий спостерігач і ракетний корабель, що рухається до джерела світла. Два спостерігачі пов'язані координатою, або простором-часом, перетворенням. Другий принцип тоді говорить нам, що незалежно від того, наскільки швидко рухається ракета, обидва спостерігачі повинні вимірювати однакову швидкість світла, що виходить від джерела. Єдиний спосіб це може статися, якщо годинник спостерігача ракети тикають з іншою швидкістю, ніж у стаціонарного спостерігача. Наскільки відрізняється? Це можна виразити в рівнянні розширення часу:

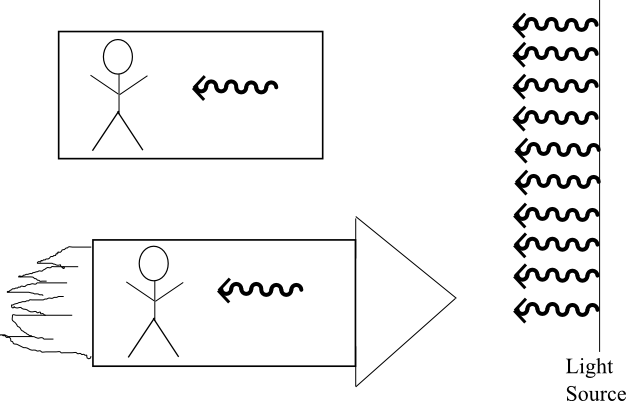
    зображення

    Вимірювання світла: Стаціонарний спостерігач вимірюватиме ту ж швидкість світла, що і спостерігач, який рухається на ракетному кораблі, навіть якщо ця ракета рухається близько до швидкості світла.

    \[\mathrm { t } _ { \mathrm { s } } = \dfrac { \mathrm { t } _ { \mathrm { m } } } { \sqrt { 1 - \left( \dfrac { \mathrm{v} ^ { 2 } } { \mathrm { c } ^ { 2 } } \right) } }\]

    Там, де tsts - час, що минув для стаціонарного спостерігача, tmtm - це час, що минув для рухомого спостерігача, а vv - швидкість ракети, виміряна від нерухомого кадру. Потім видно, що час,\(\mathrm { V } \rightarrow \mathrm { C }\) що минув у стаціонарному кадрі, йде до нескінченності. Щоб розмістити деякі цифри, нехай\(\mathrm { v } = 0.99986 \mathrm { c }\), і\(\mathrm { t } _ { \mathrm { m } } = \mathrm { 1 \; sec } \). Час, що минув в стаціонарному каркасі, тоді становить одну годину. Таким чином за кожну секунду, що жила в ракеті, стаціонарна людина живе одну годину!

    Одним з найбільш радикальних результатів розширення часу є так званий «парадокс близнюків». парадокс близнюків - це розумовий експеримент у спеціальній теорії відносності, який включає однакових близнюків. Один з близнюків відправляється в подорож в космос на ракеті, яка має швидкість близько швидкості світла. Після повернення додому близнюк виявляє, що близнюк, який залишився на Землі, постарів більше. Цей наслідок змінив уявлення про те, що старіння обов'язково постійне.

    Коефіцієнт квадратного кореня в рівнянні розширення часу дуже важливий, і ми позначимо його як:

    Цей фактор часто проявляється в спеціальній теорії відносності. Наприклад, формула скорочення довжини така:

    \[\mathrm { L } = \mathrm { L } _ { 0 } \sqrt { 1 - \left( \dfrac { \mathrm{v} } { \mathrm{c} } \right) } = \dfrac { \mathrm { L } _ { 0 } } { \gamma }\]

    де\(\mathrm{L_0}\) - довжина решти, довжина об'єкта, виміряна в спільному рухомому кадрі об'єкта, і\(\mathrm{L}\) довжина об'єкта, виміряна спостерігачем, який бачить об'єкт, що рухається зі швидкістю\(\mathrm{v}\). У нашому прикладі ракети стаціонарний спостерігач вимірює довжину ракети як меншу, ніж вимірює той, хто рухався з ракетою. Це змінило уявлення про те, що довжина об'єкта виглядатиме однаковою незалежно від системи відліку спостерігача.

    Ще одна радикальна знахідка, яка стала можливою завдяки відкриттю особливої відносності, - еквівалентність енергії і маси. У поєднанні з іншими законами фізики постулати особливої відносності передбачають, що маса і енергія пов'язані між собою:\(\mathrm{E=mc^2}\), де c - швидкість світла у вакуумі. Це змінило уявлення про те, що маса і енергія - це абсолютно різні речі і проклало шлях для ядерної енергетики та ядерної зброї.

    В якості завершального зауваження важливо відзначити, наскільки велика швидкість світла в порівнянні з повсякденним життям. Швидкість світла становить:

    \[\mathrm { c } = 3 \times 10 ^ { 8 } \mathrm { m } / \mathrm { s }\]

    Таким чином, в повсякденному житті ми\(\mathrm{γ≈1}\) і не відчуваємо значного розширення часу або скорочення довжини. Якби ми це зробили, життя було б зовсім іншим.

    Чотиривимірний простор-час

    Ми живемо в чотиривимірному простору-часі, в якому від спостерігача може залежати впорядкованість тих чи інших подій.

    навчальні цілі

    • Сформулювати основні результати спеціальної теорії відносності

    Робота в чотирьох вимірах

    Розглянемо двох спостерігачів, які рухаються один відносно одного з постійною швидкістю. Ми позначимо їх як спостерігач А і спостерігач А '. Спостерігач A встановлює просторово-часову систему координат (t, x, y, z); аналогічно, A' встановлює власну систему координат просторово-часу (t', x', y', z'). Тому обидва спостерігачі живуть у чотиривимірному світі з трьома просторовими вимірами та одним часовим виміром.

    зображення

    Дві системи координат: Дві системи координат, в яких загрунтований кадр рухається зі швидкістю v щодо негрунтованого кадру

    Вам не слід вважати дивним працювати з чотирма вимірами; будь-який час, коли вам доведеться десь зустрітися зі своїм другом, ви повинні сказати йому чотири змінні: де (три просторові координати) і коли (одна координата часу). Іншими словами, ми завжди жили в чотирьох вимірах, але поки що ви, мабуть, думали про простір і час як про абсолютно окремі.

    Рух світла в чотирьох вимірах

    Повернемося до нашого прикладу: припустимо, що в якийсь момент простору-часу з'являється промінь світла. Обидва спостерігачі вимірюють, наскільки далеко промінь пройшов у кожен момент часу і скільки часу знадобилося, щоб проїхати цю відстань. Тобто, спостерігач А вимірює:

    \(\mathrm{( \Delta t , \Delta x , \Delta y , \Delta z )}\)

    де, наприклад,\(\mathrm{\Delta t = t - t _ { 0 }}\); t - час, в яке відбулося вимірювання; а t 0 - час, в яке було включено світло.

    Аналогічно, спостерігач A 'вимірює:

    \(\left( \Delta t ^ { \prime } , \Delta x ^ { \prime } , \Delta y ^ { \prime } , \Delta z ^ { \prime } \right)\)

    де ми створили систему таким чином, щоб обидва спостерігачі домовилися\(\left( \mathrm { t } _ { 0 } , \mathrm { x } _ { 0 } , \mathrm { y } _ { 0 } , \mathrm { z } _ { 0 } \right)\). Завдяки незмінності швидкості світла обидва спостерігачі погодяться про:

    \[\dfrac { \Delta \mathrm { X } ^ { 2 } + \Delta \mathrm { Y } ^ { 2 } + \Delta \mathrm { Z } ^ { 2 } } { \Delta \mathrm { T } ^ { 2 } } = \mathrm { c } ^ { 2 } \rightarrow 0 = - \mathrm { c } ^ { 2 } \Delta \mathrm { T } ^ { 2 } + \Delta \mathrm { X } ^ { 2 } + \Delta \mathrm { Y } ^ { 2 } + \Delta \mathrm { Z } ^ { 2 }\]

    де\(\mathrm{(T,X,Y,Z)}\) посилається на координати в будь-якому кадрі. Тому існує певне правило, згідно з яким повинні слідувати всі світлові шляхи. Для загальних подій ми можемо визначити кількість:

    \[\mathrm{s} ^ { 2 } = - \mathrm{c} ^ { 2 } \Delta t ^ { 2 } + \Delta \mathrm{x} ^ { 2 } + \Delta \mathrm{y} ^ { 2 } + \Delta \mathrm{z} ^ { 2 }\]

    Цей елемент відомий як лінійний елемент і однаковий для всіх спостерігачів. (Використовуючи принципи відносності, можна довести це для загальних поділів, а не тільки світлових променів). Набір усіх координатних перетворень, які залишають вищевказану кількість інваріантними, відомі як перетворення Лоренца. Звідси випливає, що системи координат всіх фізичних спостерігачів пов'язані один з одним перетвореннями Лоренца. (Сукупність усіх перетворень Лоренца формує те, що математики називають групою, а вивчення теорії груп зробило революцію у фізиці). Для перетворення координат в перетворення є:

    \[\left. \begin{array} { l } { \mathrm { t } ^ { \prime } = \gamma \left( \mathrm { t } - \mathrm { vx } / \mathrm { c } ^ { 2 } \right) } \\ { \mathrm { x } ^ { \prime } = \gamma ( \mathrm { x } - \mathrm { vt } ) } \\ { \mathrm { y } ^ { \prime } = \mathrm { y } } \\ { \mathrm { z } ^ { \prime } = \mathrm { z } } \end{array} \right.\]

    де

    \[\gamma = \dfrac { 1 } { \sqrt { 1 - ( \mathrm{ v } / \mathrm { c } ) ^ { 2 } } }\]

    Визначаємо поділ між просторово-часовими точками наступним чином:

    \[\mathrm { s } ^ { 2 } > 0 : \text { space-like }\]

    \[\mathrm { s } ^ { 2 } < 0 : \text { time-like }\]

    \[\mathrm { s } ^ { 2 } = 0 : \text { null }\]

    Ми відокремлюємо ці події, тому що вони дуже різні. Наприклад, для просторового поділу ви завжди можете знайти координатне перетворення, яке змінює часове впорядкування подій (спробуйте довести це для прикладу в). Це явище відоме як відносність одночасності і може бути контрінтуїтивним.

    Просторово-часові поділи

    Розглянемо дві автомобільні аварії, одну в Нью-Йорку і одну в Лондоні, такі, що вони відбуваються в один і той же час в одному кадрі. У цій ситуації просторово-часовий поділ між двома подіями схоже на простір. Питання про те, чи події є одночасними, є відносним: у деяких довідкових кадрах дві аварії можуть відбуватися одночасно; в інших кадрах (в іншому стані руху щодо подій) аварія в Лондоні може статися першою; а в інших кадрах нью-йоркська аварія може статися першим. (На практиці це не впливає на нас, оскільки кадри, які перемикають порядок подій, повинні рухатися з недосяжними високими швидкостями.)

    Час-подібний і нульовий просторово-часовий поділ

    Події, які є тимчасовими або нульовими, не поділяють цю властивість, і тому існує причинно-наслідкове впорядкування між подіями, подібними до часу. Іншими словами, якщо дві події схожі на час розділені, то вони можуть впливати один на одного. Причина полягає в тому, що якщо дві просторово-часові точки є тимчасовими або нульовими розділеними, завжди можна відправити світловий сигнал з однієї точки в іншу.

    Спеціальна відносність

    Нарешті, давайте обговоримо важливий результат спеціальної відносності — що енергія ЕЕ об'єкта, що рухається зі швидкістю vv, є:

    \[\mathrm { E } = \frac { \mathrm { m } _ { 0 } \mathrm { c } ^ { 2 } } { \sqrt { 1 - ( \mathrm { v } / \mathrm { c } ) ^ { 2 } } } = \mathrm { mc } ^ { 2 }\]

    де m0m0 - маса об'єкта в стані спокою, а m=γm0m = γm0 - маса при переміщенні об'єкта. Наведена вище формула відразу показує, чому не можна подорожувати швидше швидкості світла. Як\(\mathrm { v } \rightarrow \mathrm { c } , \mathrm { m } \rightarrow \infty \), і потрібно нескінченна кількість енергії для подальшого прискорення об'єкта.

    Релятивістський Всесвіт

    Гравітація - це геометричний ефект, в якому особливу роль відіграє метрична матриця, а рух об'єктів змінюється кривим простором.

    навчальні цілі

    • Визначте фактори, що впливають на рух поблизу масивних об'єктів

    Відносність

    Особлива відносність вказує на те, що люди живуть у чотиривимірному простору-часі, де «відстань» між точками у простору-часі можна розглядати як:

    \ [\ математика {s} ^ {2} = -\ математика {c} ^ {2}\ Дельта\ математика {t} ^ {2} +\ Дельта\ математика {x} ^ {2} +\ Дельта\ математика {s} ^ {2} +\ Дельта\ математика {a} ^ {2} =\ математика {X} ^ {X} ^ {\ mathrm m {T}}\ та\ математика {X}

    Останнє рівняння являє собою матричне відношення, в якому ТТ позначає транспонування (для векторів\(\mathrm { A } ^ { \mathrm { T } } \mathrm { B } = \mathrm { A } \cdot \mathrm { B }\)),\(\mathrm{X}\) є вектор\) (\ mathrm {c}\ Delta\ mathrm {t},\ Delta\ mathrm {x},\ Delta\ mathrm {y},\ Delta\ mathrm {z})\), і\(\mathrm{η}\) являє собою матрицю:

    \[\eta = \left( \begin{array} { c c c c } { - 1 } & { 0 } & { 0 } & { 0 } \\ { 0 } & { 1 } & { 0 } & { 0 } \\ { 0 } & { 0 } & { 1 } & { 0 } \\ { 0 } & { 0 } & { 0 } & { 1 } \end{array} \right)\]

    Матриця, яка йде між двома векторами, щоб дати довжину, називається метрикою. У математиці метрична або дистанційна функція - це функція, яка визначає відстань між елементами множини. У цьому випадку множиною є простор-час, а елементи - точки в цьому простору-часі. Простір-час з β метрикою називається простором Мінковського, а η - метрикою Мінковського.

    Чотиривимірний простор-час Мінковського є лише одним з багатьох різних можливих просторів-часу (геометрії), які відрізняються своєю метричною матрицею. Довільну метричну матрицю можна позначити як gg, викликаючи питання щодо того, що представляють простори-часи з різними метриками. У 1916 році Ейнштейн знайшов важливість цих просторів-часів у своїй теорії загальної відносності.

    Загальна відносність

    Загальна теорія відносності, або загальна теорія відносності, - це геометрична теорія гравітації, опублікована Альбертом Ейнштейном в 1916 році. Це сучасний опис гравітації в сучасній фізиці. Загальна теорія відносності узагальнює спеціальну відносність і закон Ньютона всесвітнього тяжіння, забезпечуючи уніфікований опис гравітації як геометричної властивості простору і часу, або простору-часу. Зокрема, кривизна простору-часу безпосередньо пов'язана з енергією і імпульсом будь-якої матерії і випромінювання. Співвідношення задається польовими рівняннями Ейнштейна, системою рівнянь з частинними похідними.

    \[\text { g } \leftrightarrow \text { curvature } \leftrightarrow \text { Energy and Momentum }\]

    Люди можуть використовувати метрику для обчислення кривизни, а потім використовувати рівняння поля Ейнштейна, щоб пов'язати кривизну з енергією та імпульсом простору-часу. Йдучи в зворотному порядку, енергія і імпульс впливають на кривизну і простор-час. Таким чином, енергія і імпульс криві простору-часу. Простір Мінковського - це особливий простір, позбавлений матерії, і, як наслідок, він повністю плоский. Точне визначення кривизни вимагає знання вищої математики, але інтуїтивний спосіб зрозуміти це полягає в тому, що визначення прямої лінії змінюється в криволінійному просторучасі.

    Мальовничий приклад показаний на малюнку нижче, де все, що знаходиться поблизу Землі, має свій рух змінений через криволінійний простору-час. Ця зміна руху впливає на супутники, Місяць і навіть людей. Якби простір навколо Землі було рівним, люди просто відпливали б, якби стрибали вгору. Оскільки Земля змінює простор-час, люди тягнуться до Землі. По суті, гравітація - це геометричний ефект.

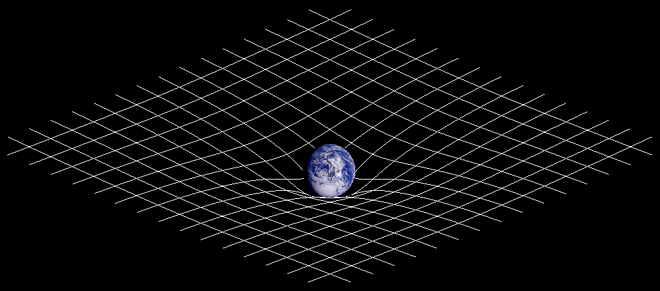
    зображення

    Кривизна простору-часу: Масивна Земля змінює кривизну простору-часу.

    Ключові моменти

    • Час відносний.
    • Довжини рухомих об'єктів відрізняються від того, якби їх довжини вимірювалися в спільному рухомому кадрі.
    • Час і простір не є незалежними.
    • Ми живемо у чотиривимірному Всесвіті; перші три виміри просторові, а четверте - час.
    • Система координат фізичних спостерігачів пов'язана один з одним за допомогою перетворень Лоренца.
    • Ніщо не може подорожувати швидше, ніж швидкість світла.
    • Метрична матриця може бути використана для обчислення кривизни простору-часу.
    • Кривизна може бути пов'язана з енергією та імпульсом за допомогою рівнянь Ейнштейна.
    • Через кривизну простору-часу змінюється рух предметів поблизу масивних об'єктів.

    Ключові умови

    • спеціальна теорія відносності: теорія, яка (нехтуючи ефектами гравітації) узгоджує принцип відносності із спостереженням про те, що швидкість світла постійна у всіх системах відліку.
    • розширення часу: Уповільнення проходження часу, яке відчувають об'єкти в русі відносно спостерігача; вимірюється лише на релятивістських швидкостях.
    • скорочення довжини: Спостерігачі вимірюють довжину рухомого об'єкта як меншу, ніж було б, якби він був нерухомим.
    • лінійний елемент: інваріантна величина в спеціальній відносності
    • Перетворення Лоренца: перетворення, що пов'язує просторово-часові координати одного кадру відліку до іншого в спеціальній теорії відносності
    • відносність одночасності: Для просторово-подібних розділених просторово-часових точок порядок часу між подіями є відносним.
    • загальна теорія відносності: теорія, що розширює спеціальну відносність і рівномірно враховує гравітаційні та прискорені рамки відліку, постулюючи, що просторово-часові криві при наявності маси.
    • Простір Мінковського: чотиривимірний плоский простор-час. Оскільки вона плоска, вона позбавлена матерії.
    • метрика: Метрика, або функція відстані, - це функція, яка визначає відстань між елементами множини.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ