Skip to main content
LibreTexts - Ukrayinska

27.2: Наслідки спеціальної відносності

  1. Last updated
  2. Save as PDF
  • Page ID
    75118

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Сформулювати висновки теорії спеціальної відносності, зазначивши припущення, які були зроблені при її виведенні

    Відносність одночасності - це поняття, що одночасність - чи відбуваються дві події одночасно - не є абсолютною, але залежить від системи відліку спостерігача.

    Відповідно до теорії особливої відносності, неможливо сказати в абсолютному сенсі, чи відбуваються дві різні події одночасно, якщо ці події розділені в просторі, наприклад, автомобільна аварія в Лондоні та інша в Нью-Йорку. Питання про те, чи є події одночасними, є відносним: в деяких еталонних кадрах дві аварії можуть відбуватися одночасно, в інших кадрах (в іншому стані руху щодо подій) аварія в Лондоні може статися першою, а все ж в інших кадрах спочатку може статися аварія в Нью-Йорку. Якщо дві події причинно пов'язані («подія A викликає подію B»), то відносність одночасності зберігає причинно-наслідковий порядок (тобто «подія A викликає подію B» у всіх системах відліку).

    Якщо ми уявляємо, що один контрольний кадр призначає точно однаковий час двом подіям, які знаходяться в різних точках простору, опорна рамка, яка рухається відносно першого, як правило, призначає різний час для двох подій. Це проілюстровано парадоксом сходів, думковим експериментом, який використовує приклад сходів, що рухаються з великою швидкістю через гараж.

    Математична форма відносності одночасності («місцевий час») була введена Хендріком Лоренцем у 1892 році, а фізично інтерпретована (до першого порядку у v/c) в результаті синхронізації з використанням світлових сигналів Анрі Пуанкаре в 1900 році. Однак і Лоренц, і Пуанкаре базували свої уявлення про ефір як бажану, але непомітну систему відліку, і продовжували розрізняти «справжній час» (в ефірі) та «очевидний» час для рухомих спостерігачів.

    У 1905 році Альберт Ейнштейн відмовився від (класичного) ефіру і підкреслив значення відносності одночасності для нашого розуміння простору і часу. Він вивів збій абсолютної одночасності з двох заявлених припущень: 1) принцип відносності—еквівалентність інерційних кадрів, такий, що закони фізики застосовуються однаково у всіх інерційних системах координат; 2) сталість швидкості світла, виявленої в порожньому просторі, незалежно від відносний рух його джерела.

    зображення

    Спостерігач, що стоїть на платформі: Опорна рамка спостерігача, що стоїть на платформі (скорочення довжини не зображено).

    зображення

    Спостерігач на борту поїзда: Експеримент поїзда та платформи з опорної системи спостерігача на борту поїзда.

    Розширення часу

    Розширення часу - це фактична різниця часу, що минув між двома подіями, виміряна спостерігачами, що рухаються відносно один одного.

    навчальні цілі

    • Поясніть, чому розширення часу можна ігнорувати в повсякденному житті

    Розширення часу - це фактична різниця часу, що минув між двома подіями, виміряна спостерігачами або рухаються відносно один одного.

    Наприклад, два ракетні кораблі (A і B), що перевищують один одного в космосі, зазнають розширення часу. Якби вони якось мали чітке уявлення про кораблі один одного, кожен екіпаж бачив би годинник та рух інших як занадто повільно. Тобто всередині системи відліку корабля А все рухається нормально, але все на кораблі B, здається, рухається повільніше (і навпаки).

    З місцевої точки зору час, зареєстрований годинниками, які перебувають у спокої щодо локальної системи відліку (і далеко не будь-якої гравітаційної маси), завжди проходить з однаковою швидкістю. Іншими словами, якщо новий корабель, корабель C, подорожує поряд з кораблем А, він «в спокої» відносно корабля А. З точки зору корабля А, новий корабель C також здасться нормальним.

    Формула визначення тимчасової дилатації така:\(\mathrm{\Delta t ^ { \prime } = \gamma \Delta t = \frac { \Delta t } { \sqrt { 1 - v ^ { 2 } / c ^ { 2 } } }}\)

    де Δt - часовий проміжок між двома спільними подіями (тобто відбуваються в одному місці) для спостерігача в якомусь інерційному кадрі (наприклад, кліки на його годиннику), це відомо як належний час, Δt - проміжок часу між тими самими подіями, виміряний іншим спостерігачем, інерційно рухаючись зі швидкістю v по відношенню до колишнього спостерігача v - відносна швидкість між спостерігачем і рухомим годинником, c - швидкість світла, а\(\mathrm{\gamma = \frac { 1 } { \sqrt { 1 - v ^ { 2 } / c ^ { 2 } } }}\)

    є фактором Лоренца. Таким чином, тривалість тактового циклу рухомого годинника виявляється збільшеною: він вимірюється як «повільно працює». Зверніть увагу, що для швидкостей нижче 1/10 швидкості світла коефіцієнт Лоренца дорівнює приблизно 1. Таким чином, ефекти розширення часу надзвичайно малі і можуть бути спокійно ігноровані в повсякденному житті. Вони стають важливими лише тоді, коли об'єкт наближається до швидкості близько 30 000 км/с (1/10 швидкості світла).

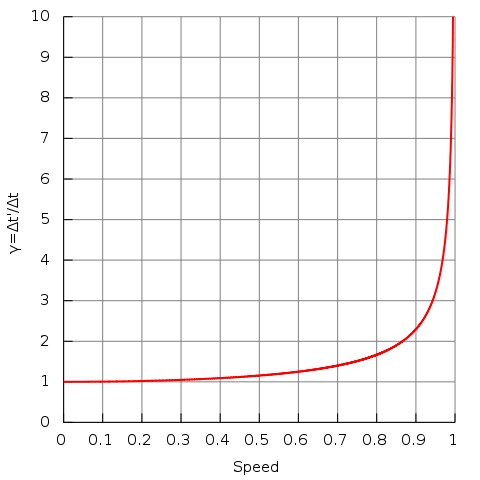
    зображення

    Фактор Лоренца: фактор Лоренца як функція швидкості (в природних одиницях, де c = 1). Зверніть увагу, що для малих швидкостей (менше 0,1) γ дорівнює приблизно 1.

    Ефекти розширення часу: парадокс близнюків та розпад мюону

    Парадокс близнюків - це мислимий експеримент: один близнюк здійснює подорож у космос і повертається додому, щоб виявити, що близнюк залишився у віці більше.

    навчальні цілі

    • Поясніть парадокс близнюків в стандартних рамках спеціальної теорії відносності

    Парадокс близнюків - це розумовий експеримент у спеціальній теорії відносності за участю однакових близнюків, один з яких здійснює подорож у космос на швидкісній ракеті і повертається додому, щоб виявити, що близнюк, який залишився на Землі, постарів більше.

    Це відбувається тому, що спеціальна відносність показує, що чим швидше подорожує, тим повільніше рухається час для них.

    Цей результат виглядає загадковим, тому що кожен близнюк бачить іншого близнюка як подорожі, і тому, відповідно до наївного застосування розширення часу, кожен повинен парадоксально знайти іншого, щоб старіти повільніше. Іншими словами, з точки зору ракетного корабля, земля відходить від корабля і з точки зору землі ракета їде далеко.

    Однак цей сценарій може бути вирішений в стандартних рамках особливої теорії відносності (адже близнюки не рівнозначні; космічний близнюк відчував додаткове, асиметричне прискорення при перемиканні напрямку на повернення додому), і тому не є парадоксом в сенсі логічного протиріччя.

    Земля і корабель не знаходяться в симетричному взаємозв'язку: незалежно від того, розглядаємо ми ситуацію з точки зору Землі або корабля, корабель відчуває додаткові сили прискорення. Судно має поворот, в якому він прискорюється і змінює напрямок, тоді як земля цього не робить. Оскільки немає симетрії, не парадоксально, якщо один близнюк молодший за іншого. Проте парадокс близнюків корисний як демонстрація того, що особлива відносність є самоузгодженою.

    На просторово-часовій діаграмі, намальованій для опорного кадру земного близнюка, світова лінія цього близнюка збігається з вертикальною віссю (його положення постійне в просторі, рухається тільки в часі). На першій нозі поїздки другий близнюк рухається вправо (чорна похила лінія); а на другій нозі - назад вліво. Сині лінії показують площини одночасності для подорожуючого близнюка під час першого етапу подорожі; червоні лінії, під час другої ноги. Безпосередньо перед поворотом, подорожуючий близнюк обчислює вік земного близнюка, вимірюючи інтервал вздовж вертикальної осі від початку до верхньої синьої лінії. Відразу після повороту, якщо він перерахує, він виміряє інтервал від початку до нижньої червоної лінії. У певному сенсі під час розвороту площина одночасності перескакує з синього на червоний і дуже швидко змітає великий відрізок світової лінії земного близнюка. Подорожуючий близнюк вважає, що в епоху земного близнюка відбувся стрибок розриву.

    зображення

    Просторово-часова діаграма парадоксу близнюків: Просторово-часова діаграма парадоксу близнюків. Час відносне, але обидва близнюки не рівнозначні (корабель відчуває додаткове прискорення до зміни напрямку руху).

    скорочення довжини

    Об'єкти, які рухаються, зазнають скорочення довжини вздовж розмірності руху; цей ефект значний лише при релятивістських швидкостях.

    навчальні цілі

    • Поясніть, чому скорочення довжини можна ігнорувати в повсякденному житті

    Скорочення довжини - це фізичне явище зменшення довжини, виявлене спостерігачем об'єктів, які рухаються з будь-якою ненульовою швидкістю відносно цього спостерігача. Скорочення довжини виникає через те, що швидкість світла в вакуумі постійна в будь-якому кадрі відліку. Враховуючи це, а також деякі геометричні міркування, ми покажемо, як впливає сприймається час і тривалість.

    Приклад\(\PageIndex{1}\):

    Уявімо собі просту годинникову систему, яка складається з двох дзеркал A і B у вакуумі. Світловий імпульс відскакує між двома дзеркалами. Поділ дзеркал дорівнює L, а годинник тикає один раз кожен раз, коли світловий імпульс потрапляє на задане дзеркало. А тепер уявіть, що годинник знаходиться в стані спокою. Час, який знадобиться для того, щоб світловий імпульс перейшов від дзеркала А до дзеркала B, а потім назад до дзеркала А можна описати:

    \[\Delta t = \dfrac { 2 \mathrm { L } } { c }\]

    де c - швидкість світла. Тепер уявіть, що годинник рухаються в горизонтальному напрямку щодо нерухомого спостерігача. Світловий імпульс випромінюється від дзеркала А. До стаціонарного спостерігача виявляється, що світловий імпульс має довший шлях для подорожі, оскільки до того часу, коли світло досягає дзеркала В, годинник вже дещо перемістився в горизонтальному напрямку. Це той самий випадок і для світлового імпульсу на зворотному шляху. Стаціонарний спостерігач сприйме, що він забере світло в цілому:

    зображення

    Геометрія для годинника в стані спокою: Це ілюструє шлях, який світло повинен пройти, коли годинник знаходиться в стані спокою.

    \[\Delta t ^ { \prime } = \frac { 2 D } { c }\]

    пройти його шлях. Ми бачимо, що D довше, ніж L, так що це означає, що.

    зображення

    Геометрія для рухомого годинника: Це ілюструє шлях, який світло повинен пройти, коли годинник рухається з точки зору стаціонарного спостерігача.

    Приклад\(\PageIndex{2}\):

    Встановлено, що в системі відліку, яка рухається щодо годинника (стаціонарний спостерігач рухається в рамці відліку годинника), годинник, здається, працює повільніше. Тепер уявімо, що ми хочемо виміряти довжину лінійки. Цього разу давайте уявимо, що ви рухаєтеся зі швидкістю v. Ви можете математично визначити довжину лінійки у вашій системі відліку (L '), помноживши свою швидкість (v) на час, коли ви сприймаєте, що вам потрібно пройти повз лінійку (t'). Висловлюючи це у формі рівняння, L '= vt'. Тепер, якщо хтось у кадрі відпочинку лінійки хотів визначити довжину лінійки, вони могли б зробити наступне. Вони могли математично визначити довжину лінійки у своїй системі відліку (L), помноживши вашу швидкість (v) на час, коли вони сприймають, що вам потрібно пройти повз лінійки (t). Це виражається в наступному рівнянні: L = vt. Так само, як і в поясненні годинника, лінійка, здається, рухається у вашій системі відліку, тому t буде довшим за t '(ваш часовий інтервал). Отже, довжина лінійки буде здаватися коротшою у вашій рамці відліку (сталося явище скорочення довжини).

    Ефект скорочення довжини незначний на повсякденних швидкостях і його можна ігнорувати для всіх регулярних цілей. Скорочення довжини стає помітним при значній частці швидкості світла (як показано на малюнку) при скороченні лише в напрямку, паралельному напрямку, в якому рухається спостережуване тіло.

    зображення

    Спостережувана довжина об'єкта: Спостережувана довжина об'єкта в спокої та з різною швидкістю

    Приклад\(\PageIndex{3}\):

    Наприклад, при швидкості 13 400 000 м/с (30 млн миль/год, .0447 c) довжина становить 99,9 відсотка довжини в спокої; при швидкості 42 300 000 м/с (95 млн миль/год, 0,141 с) довжина все ще становить 99 відсотків. У міру наближення величини швидкості до швидкості світла ефект стає домінуючим. Математична формула скорочення довжини така:

    \[\mathrm { L } = \dfrac { \mathrm { L } _ { 0 } } { \gamma ( v ) } = \mathrm { L } _ { 0 } \sqrt { 1 - \dfrac { v ^ { 2 } } { \mathrm { c } ^ { 2 } } }\]

    де L 0 - належна довжина (довжина об'єкта в його кадрі спокою); L - довжина, яку спостерігає спостерігач у відносному русі щодо об'єкта; v - відносна швидкість між спостерігачем і рухомим об'єктом; c - швидкість світла; а коефіцієнт Лоренца визначається як:

    \[\gamma ( v ) = \dfrac { 1 } { \sqrt { 1 - v ^ { 2 } / c ^ { 2 } } }\]

    У цьому рівнянні передбачається, що об'єкт паралельний його лінії руху. Для спостерігача при відносному русі довжина об'єкта вимірюється шляхом віднімання одночасно виміряних відстаней обох кінців об'єкта. Спостерігач у спокої розглядає об'єкт, що рухається дуже близько до швидкості світла, буде спостерігати довжину об'єкта у напрямку руху як дуже близьку до нуля.

    Ключові моменти

    • Відповідно до теорії особливої відносності, неможливо сказати в абсолютному сенсі, чи відбуваються дві різні події одночасно, якщо ці події розділені у просторі.
    • Математична форма відносності одночасності була введена Хендріком Лоренцем і фізично інтерпретована Анрі Пуанкаре. Концепції базувалися на ефірі як бажаній, але невиявленій системі відліку.
    • Альберт Ейнштейн вивів збій абсолютної одночасності з двох припущень: 1) принципу відносності; 2) сталості швидкості світла, виявленої в порожньому просторі, незалежно від відносного руху його джерела.
    • Ефекти розширення часу надзвичайно малі для швидкостей нижче 1/10 швидкості світла, і їх можна безпечно ігнорувати в повсякденному житті.
    • Ефекти розширення часу стають важливими, коли об'єкт наближається до швидкості близько 30 000 км/с (1/10 швидкості світла).
    • Формула визначення тимчасової дилатації така:\(\mathrm{\Delta t ^ { \prime } = \frac { \Delta t } { \sqrt { 1 - v ^ { 2 } / c ^ { 2 } }} }\).
    • З наївного застосування розширення часу, кожен близнюк повинен парадоксально знайти іншого, щоб старіти повільніше.
    • Сценарій вирішується в стандартних рамках особливої теорії відносності: близнюки не рівнозначні, космічний близнюк відчуває додаткове, асиметричне прискорення при перемиканні напрямку на повернення додому.
    • Парадокс близнюків корисний як демонстрація того, що особлива відносність є самопослідовною.
    • Скорочення довжини незначне на повсякденних швидкостях і може бути проігноровано для всіх регулярних цілей.
    • Скорочення довжини стає помітним при значній частці швидкості світла при скороченні тільки в напрямку, паралельному напрямку, в якому рухається спостережуване тіло.
    • Спостерігач у спокої розглядає об'єкт, що рухається дуже близько до швидкості світла, буде спостерігати довжину об'єкта у напрямку руху як дуже близько нуля.

    Ключові умови

    • ефір: речовина або поле, що заповнює простір, вважається необхідним як середовище передачі для поширення електромагнітних або гравітаційних сил.
    • спеціальна теорія відносності: теорія, яка (нехтуючи ефектами гравітації) узгоджує принцип відносності із спостереженням про те, що швидкість світла постійна у всіх системах відліку.
    • швидкість світла: швидкість електромагнітного випромінювання в ідеальному вакуумі: рівно 299,792,458 метрів в секунду за визначенням
    • розширення часу: Уповільнення проходження часу, яке відчувають об'єкти в русі відносно спостерігача; вимірюється лише на релятивістських швидкостях.
    • Коефіцієнт Лоренца: Коефіцієнт, який використовується в спеціальній теорії відносності, для обчислення ступеня розширення часу, скорочення довжини та релятивістської маси об'єкта, що рухається відносно спостерігача.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ