Skip to main content
LibreTexts - Ukrayinska

26.1: Суперпозиція та перешкоди

  1. Last updated
  2. Save as PDF
  • Page ID
    74633

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    навчальні цілі

    • Контраст ефектів конструктивного і руйнівного втручання

    Умови хвильової інтерференції

    Інтерференція - це явище, при якому дві хвилі накладаються, утворюючи результуючу хвилю більшої чи меншої амплітуди. Його вплив можна спостерігати у всіх типах хвиль (наприклад, світлових, акустичних хвиль і водних хвиль). Інтерференція зазвичай стосується взаємодії хвиль, які корелюють (когерентні) один з одним, оскільки вони походять від одного джерела, або вони мають однакову або майже однакову частоту. Коли дві або більше хвиль падають на одну точку, сумарне зміщення в цій точці дорівнює векторній сумі переміщень окремих хвиль. Якщо гребінь однієї хвилі зустрічається з гребенем іншої хвилі тієї ж частоти в тій же точці, то величина зміщення - це сума окремих величин. Це конструктивна перешкода і виникає, коли різниця фаз між хвилями кратна 2π. Руйнівна перешкода виникає, коли гребінь однієї хвилі зустрічається з жолобом іншої хвилі. При цьому величина переміщень дорівнює різниці окремих величин, і виникає, коли ця різниця непарна кратна π. Приклади конструктивного і деструктивного втручання наведено в. Якщо різниця між фазами є проміжною між цими двома крайностями, то величина зміщення підсумованих хвиль лежить між мінімальним і максимальним значеннями.

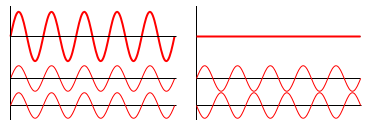
    зображення

    Хвильова інтерференція: приклади конструктивної (лівої) та деструктивної (правої) хвильової інтерференції

    Хвильові інтерференції: Короткий вступ до конструктивної та руйнівної хвильової інтерференції та принципу суперпозиції.

    Проста форма хвильової інтерференції спостерігається, коли дві хвилі однакової частоти (також звані плоскою хвилею) перетинаються під кутом, як показано в. Припускаючи, що дві хвилі знаходяться у фазі в точці B, то відносна фаза змінюється вздовж осі x. Різниця фаз в точці А задається:

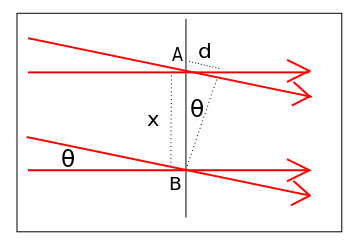
    зображення

    Інтерференція плоских хвиль: Геометричне розташування двох плоских хвиль інтерференції.

    \[\Delta \varphi = \dfrac { 2 \pi \mathrm { d } } { \lambda } = \frac { 2 \pi \mathrm { x } \sin \theta } { \lambda }\]

    Конструктивне втручання виникає, коли хвилі знаходяться в фазі, або

    \[\dfrac { x \sin \theta } { \lambda } = 0 , \pm 1 , \pm 2 , \ldots \]

    Руйнівні перешкоди виникають, коли хвилі знаходяться на половині циклу поза фазою, або

    \[\dfrac { x \sin \theta } { \lambda } = \pm \frac { 1 } { 2 } , \pm \frac { 3 } { 2 } , \ldots\]

    Відображення через зміну фази

    Світло проявляє хвильові характеристики в різних середовищах, а також у вакуумі. Коли світло переходить від вакууму до якогось середовища (наприклад, води), його швидкість і довжина хвилі змінюються, але його частота f залишається незмінною. Швидкість світла в середовищі дорівнює v = c/n, де n - показник заломлення. Наприклад, вода має показник заломлення n = 1,333. Коли світло відбивається від середовища з більш високим показником заломлення, гребені відбиваються, оскільки жолоби і жолоби відбиваються як гребені. Іншими словами, хвиля зазнає 180 градусів зміни фази при відображенні, а відбитий промінь «стрибає» вперед на половину довжини хвилі.

    Повітряний клин

    Повітряний клин - це простий інтерферометр, який використовується для візуалізації порушення хвильового фронту після поширення через тестовий об'єкт.

    навчальні цілі

    • Опишіть, як повітряний клин використовується для візуалізації порушення хвильового фронту після проагації

    Повітряний клин

    Повітряний клин - одна з найпростіших конструкцій зсувних інтерферометрів, що використовуються для візуалізації порушення хвильового фронту після поширення через тестовий об'єкт. Повітряний клин можна використовувати майже з будь-яким джерелом світла, включаючи некогерентне біле світло. Інтерферометр складається з двох оптичних скляних клинів (~2-5 градусів), зсунутих разом, а потім трохи відокремлених з одного боку, щоб створити тонкий клин повітряного зазору. Приклад повітряного клинового інтерферометра показаний в.

    зображення

    Повітряний клин: Приклад повітряного клинового інтерферометра

    Повітряний зазор між двома скляними пластинами має дві унікальні властивості: він дуже тонкий (мікрометрова шкала) і має ідеальну площинність. Через цей надзвичайно тонкий повітряний зазор, повітряний клиновий інтерферометр був успішно використаний в експериментах з фемтосекундними лазерами високої потужності.

    Падаючий промінь світла стикається з чотирма межами, при яких індекс заломлення середовища змінюється, викликаючи чотири відбиті пучки (або відбиття Френеля), як показано в. Перше відображення відбувається при попаданні променя в першу скляну пластину. Друге відображення відбувається, коли промінь виходить з першої пластини і потрапляє в повітряний клин, а третє відображення відбувається, коли промінь виходить з повітряного клина і потрапляє в другу скляну пластину. Четвертий промінь відбивається при зіткненні з кордоном другої скляної пластини. Кут повітряного клину між другим і третім відбиттями Френеля можна регулювати, змушуючи відбиті світлові промені конструктивно та руйнівно заважати та створювати візерунок бахроми. Щоб мінімізувати аберації зображення одержуваних бахром, кутову площину скляних клинів потрібно розташувати ортогонально до кутової площини повітряного клина.

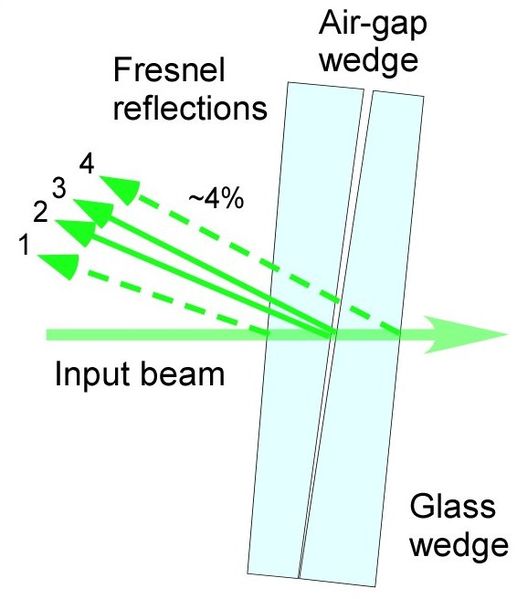
    зображення

    Світлові відбиття всередині повітряного клинового інтерферометра: шлях променя всередині повітряного клинового інтерферометра

    Кільця Ньютона

    Кільця Ньютона являють собою ряд концентричних кіл, центрованих в точці зіткнення між сферичною і плоскою поверхнею.

    навчальні цілі

    • Застосовуйте кільця Ньютона для визначення світлових характеристик лінзи

    Кільця Ньютона

    У 1717 році Ісаак Ньютон вперше проаналізував інтерференційну картину, спричинену відображенням світла між сферичною поверхнею та сусідньою плоскою поверхнею. Хоча вперше спостерігав Роберт Гук в 1664 році, ця закономірність називається кільцями Ньютона, оскільки Ньютон першим проаналізував і пояснив явища. Кільця Ньютона виглядають у вигляді ряду концентричних кіл, зосереджених у точці контакту між сферичною та плоскою поверхнями. При розгляді з однотонним світлом кільця Ньютона виглядають у вигляді чергуються яскравих і темних кілець; при погляді з білим світлом спостерігається концентричний кільцевий малюнок кольорів веселки. Приклад кілець Ньютона при огляді білим світлом показаний на малюнку нижче.

    зображення

    Кільця Ньютона в краплі води: кільця Ньютона видно в двох плоско-опуклих лінзах з їх плоскими поверхнями в контакті. Одна поверхня злегка опукла, створюючи кільця. При білому світлі кільця мають райдужний колір, оскільки різні довжини хвиль кожного кольору заважають у різних місцях.

    Світлові кільця викликані конструктивним втручанням між світловими променями, відбитими від обох поверхонь, тоді як темні кільця викликані руйнівними перешкодами. Зовнішні кільця розташовані ближче, ніж внутрішні, оскільки нахил криволінійної поверхні лінз збільшується назовні. Радіус N-го яскравого кільця задається:

    \[\mathrm { r } _ { \mathrm { N } } = \left[ \left( \mathrm { N } - \dfrac { 1 } { 2 } \lambda \mathrm { R } \right) \right] ^ { 1 / 2 }\]

    де N - яскраво-кільцеве число, R - радіус кривизни лінзи, через яку проходить світло, а λ - довжина хвилі світла, що проходить через скло.

    Поверх плоскої скляної поверхні розміщується сферична лінза. Падаючий промінь світла проходить через вигнуту лінзу до тих пір, поки не доходить до межі склоповітря, в якій точці він переходить від області з вищим показником заломлення n (скло) до області нижнього n (повітря). На цій межі деяке світло передається в повітря, в той час як деяке світло відбивається. Світло, яке передається в повітря, не відчуває зміни фази і проходить відстань, d, перш ніж воно відбивається на плоскій скляній поверхні внизу. Ця друга межа повітряного скла надає зсув фази напівперіоду відбитого світлового променя, оскільки повітря має нижчий n, ніж скло. Два відбиті світлові промені тепер рухаються в тому ж напрямку, щоб бути виявлені. Коли людина отримує далі від точки, в якій дві поверхні торкаються, відстань d збільшується, оскільки лінза вигинається від плоскої поверхні.

    зображення

    Формування інтерференційних бахром: Цей малюнок показує, як утворюються інтерференційні смуги.

    Якщо різниця довжини шляху між двома відбитими променями світла є непарною кратною довжині хвилі, розділеної на два, λ /2, відбиті хвилі будуть 180 градусів поза фазою і руйнівно заважати, викликаючи темну бахрому. Якщо різниця довжини шляху є парною кратною λ /2, відбиті хвилі будуть перебувати в фазі один з одним. Конструктивне втручання двох відбитих хвиль створює яскраву бахрому.

    Ключові моменти

    • Коли дві або більше хвиль падають на одну точку, сумарне зміщення в цій точці дорівнює векторній сумі переміщень окремих хвиль.
    • Світло проявляє хвильові характеристики в різних середовищах, а також у вакуумі. Коли світло переходить від вакууму до якогось середовища, як вода, його швидкість і довжина хвилі змінюються, але його частота f залишається незмінною.
    • Коли світло відбивається від середовища з більш високим показником заломлення, гребені відбиваються, оскільки жолоби і жолоби відбиваються як гребені. Іншими словами, хвиля зазнає 180 градусів зміни фази при відображенні, а відбитий промінь «стрибає» вперед на половину довжини хвилі.
    • Інтерферометр повітряного клина складається з двох оптичних скляних клинів (~2-5 градусів), зсунутих разом, а потім трохи відокремлених з одного боку, щоб створити тонкий клин повітряного зазору.
    • Повітряний зазор між двома скляними пластинами має дві унікальні властивості: він дуже тонкий (мікрометрова шкала) і має ідеальну площинність.
    • Щоб мінімізувати аберації зображення одержуваних бахром, кутову площину скляних клинів потрібно розташувати ортогонально до кутової площини повітряного клина.
    • При розгляді з однотонним світлом кільця Ньютона виглядають у вигляді чергуються яскравих і темних кілець; при погляді з білим світлом спостерігається концентричний кільцевий малюнок кольорів веселки.
    • Якщо різниця довжини шляху між двома відбитими променями світла є непарною кратною довжині хвилі, розділеній на два, λ/2, відбиті хвилі будуть 180 градусів поза фазою і руйнівно заважати, викликаючи темну бахрому.
    • Якщо різниця довжини шляху є парною кратною λ/2, відбиті хвилі будуть в фазі один з одним. Конструктивне втручання двох відбитих хвиль створює яскраву бахрому.

    Ключові умови

    • когерентний: хвиль, що мають однаковий напрямок, довжину хвилі та фазу, як світло в лазері.
    • плоска хвиля: хвиля постійної частоти, хвилі якої (поверхні постійної фази) є нескінченними паралельними площинами постійної амплітуди від піку до піку, нормальної вектору фазової швидкості.
    • ортогональні: з двох об'єктів, під прямим кутом; перпендикулярно один одному.
    • інтерферометр: будь-який з декількох приладів, які використовують інтерференцію хвиль для визначення довжин хвиль і швидкостей хвиль, визначення показників заломлення та вимірювання малих відстаней, температурних змін, напружень та багатьох інших корисних вимірювань.
    • довжина хвилі: Довжина одного циклу хвилі, яка вимірюється відстанню між одним піком або жолобом хвилі та наступним; вона часто позначається у фізиці як λ, і відповідає швидкості хвилі, поділеній на її частоту.
    • лінза: об'єкт, зазвичай виготовлений зі скла, який фокусує або дефокусує світло, що проходить через нього
    • монохроматичний: описує промінь світла з однією довжиною хвилі (тобто одного конкретного кольору або частоти).

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ