Skip to main content
LibreTexts - Ukrayinska

26.2: Дифракція

  1. Last updated
  2. Save as PDF
  • Page ID
    74631

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    цілі навчання

    • Сформулюйте принцип Гюйгенса

    Огляд

    Принцип Гюйгенса-Френеля стверджує, що кожна точка на хвильовому фронті є джерелом хвилетів. Ці вейвлети поширюються в прямому напрямку, з тією ж швидкістю, що і вихідна хвиля. Новий хвильовий фронт є лінією дотичною до всіх хвилетів.

    Фон

    Крістіан Гюйгенс був голландським вченим, який розробив корисну методику визначення того, як і де поширюються хвилі. У 1678 році він запропонував, щоб кожна точка, до якої торкається світлове збудження, сама по собі стає джерелом сферичної хвилі. Сума вторинних хвиль (хвиль, які є результатом порушення) визначає форму нової хвилі. показує вторинні хвилі, що рухаються вперед від точки їх походження. Він зміг придумати пояснення лінійного і сферичного поширення хвиль, і вивести закони відображення і заломлення (охоплені в попередніх атомах), використовуючи цей принцип. Однак він не зміг пояснити, що широко відомо як дифракційні ефекти. Дифракційні ефекти - це відхилення від прямолінійного поширення, що виникає, коли світло стикається з краями, екранами та отворами. Ці ефекти пояснив в 1816 році французький фізик Августин-Жан Френель.

    зображення

    Прямий хвильовий фронт: принцип Гюйгенса застосовується до прямого хвильового фронту. Кожна точка на хвильовому фронті випромінює напівкруглий вейвлет, який рухається на відстань s=vt. Новий хвильовий фронт є прямою дотичною до хвилетів.

    Принцип Гюйгенса

    На малюнку 1 показаний простий приклад принципу дифракції Гюйгенса. Принцип можна показати за допомогою рівняння нижче:

    \[\mathrm { s } = \mathrm { v } \mathrm { t }\]

    де s - відстань, v - швидкість поширення, а t - час.

    Кожна точка на хвильовому фронті випромінює хвилю зі швидкістю, v. Випускаються хвилі напівкруглі, і виникають в t, час пізніше. Новий хвильовий фронт дотичний до хвилетів. Цей принцип працює для всіх типів хвиль, а не тільки для легких хвиль. Принцип корисний при описі відображення, заломлення та перешкоди. показує візуально, як Принцип Гюйгенса може бути використаний для пояснення відображення, і показує, як його можна застосувати до заломлення.

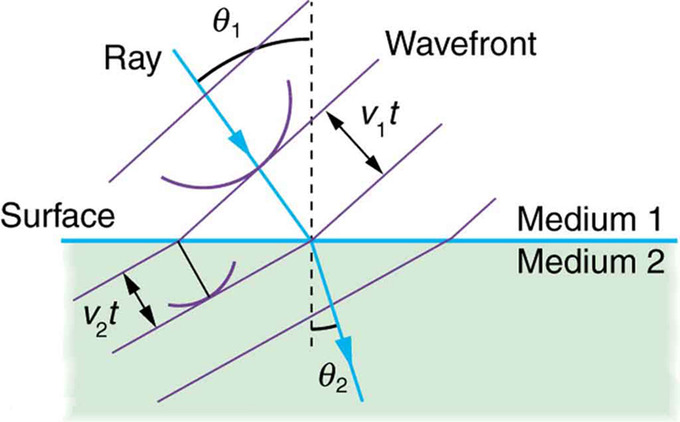
    зображення

    Заломлення Гюйгенса: принцип Гюйгенса застосовується до прямого хвильового фронту, що рухається від одного середовища до іншого, де його швидкість менша. Промінь згинається в бік перпендикуляра, так як хвилети мають меншу швидкість у другому середовищі.

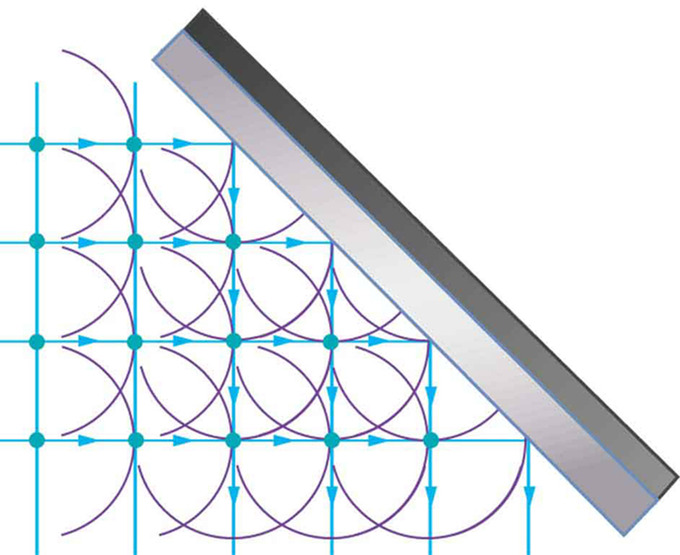
    зображення

    Відображення: принцип Гюйгенса застосований до прямого хвильового фронту, що вражає дзеркало. Показані хвилі випромінювалися, коли кожна точка на хвильовому фронті вдарила по дзеркалу. Дотична до цих хвилетів показує, що новий хвильовий фронт був відбитий під кутом, рівним куту падіння. Напрямок поширення перпендикулярно хвильовому фронту, як показано стрілками, спрямованими вниз.

    Приклад\(\PageIndex{1}\):

    Цей принцип насправді те, що ви часто бачили або переживали, але просто не усвідомлюєте. Хоча цей принцип застосовується до всіх типів хвиль, його легше пояснити за допомогою звукових хвиль, оскільки звукові хвилі мають більші довжини хвиль. Якщо хтось грає музику у своїй кімнаті, із закритими дверима, можливо, ви не зможете почути її під час проходження повз кімнати. Однак, якщо цій людині, де відкрити свої двері під час відтворення музики, ви могли почути її не тільки прямо перед відкриттям дверей, але і на значній відстані вниз по залу в обидві сторони. це прямий ефект дифракції. Коли світло проходить через набагато менші отвори, звані щілинами, принцип Гюйгенса показує, що світло вигинається подібно до того, як це робить звук, просто в набагато меншому масштабі. Ми розглянемо в більш пізніх атомах однощілинну дифракцію і подвійну щілинну дифракцію, але поки що просто важливо, щоб ми розуміли основну концепцію дифракції.

    Дифракція

    Як ми пояснювали в попередньому пункті, дифракція визначається як вигин хвилі навколо країв отвору або перешкоди.

    Експеримент Янга з подвійною щілиною

    Експеримент з подвійною щілиною, який також називають експериментом Янга, показує, що матерія та енергія можуть відображати як хвильові, так і характеристики частинок.

    цілі навчання

    • Поясніть, чому експеримент Янга більш надійний, ніж Гюйгенс

    Експеримент з подвійною щілиною, який також називають експериментом Янга, показує, що матерія та енергія можуть відображати як хвильові, так і характеристики частинок. Як ми обговорювали в атомі про принцип Гюйгенса, Крістіан Гюйгенс довів у 1628 році, що світло - це хвиля. Але деякі люди не погоджувалися з ним, особливо Ісаак Ньютон. Ньютон вважав, що колір, інтерференції та дифракційні ефекти потребують кращого пояснення. Люди не сприймали теорію про те, що світло - хвиля до 1801 року, коли англійський фізик Томас Янг виконав свій експеримент з подвійною щілиною. У своєму експерименті він послав світло через дві близько розташовані вертикальні щілини і спостерігав за отриманим малюнком на стіні за ними. Візерунок, який вийшов, можна побачити в.

    зображення

    Експеримент з подвійною щілиною Янга: Світло надсилається через дві вертикальні щілини і дифрагується в візерунок вертикальних ліній, розкинутих горизонтально. Без дифракції та перешкод світло просто зробив би дві лінії на екрані.

    Двійність хвильових частинок

    Хвильові характеристики світла змушують світло проходити крізь щілини і заважати собі, створюючи світлі та темні ділянки на стіні за щілинами. Світло, що з'являється на стіні за щілинами, розсіюється і поглинається стіною, що є характеристикою частки.

    Експеримент Янга

    Чому експеримент Янга був набагато більш надійним, ніж Гюйгенс? Тому що, хоча Гюйгенс був правильним, він не міг продемонструвати, що світло діяло як хвиля, тоді як експеримент з подвійною щілиною показує це дуже чітко. Оскільки світло має відносно короткі довжини хвиль, щоб показати хвильові ефекти, він повинен взаємодіяти з чимось невеликим - маленькі, близько розташовані щілини Янга працювали.

    У прикладі використовується два когерентних джерела світла однієї монохроматичної довжини хвилі для простоти. (Це означає, що джерела світла були в одній фазі.) Дві щілини змушують два когерентних джерела світла перешкоджати один одному або конструктивно, або руйнівно.

    Конструктивні та руйнівні хвильові перешкоди

    Конструктивна хвильова інтерференція виникає, коли хвилі заважають один одному від гребеня до гребеня (пік-пік) або жолоба до корита (долина до долини), і хвилі точно перебувають у фазі один з одним. Це підсилює результуючу хвилю. Руйнівна хвильова інтерференція виникає, коли хвилі заважають один одному від гребеня до корита (пік-долина) і точно поза фазою один з одним. Це скасовує будь-яку хвилю і призводить до відсутності світла. Ці поняття показані в. Слід зазначити, що в цьому прикладі використовується одна монохроматична довжина хвилі, яка не зустрічається в реальному житті; більш практичний приклад показаний в.

    зображення

    Практичні конструктивні та руйнівні хвильові перешкоди: Подвійні щілини створюють два когерентних джерела хвиль, які заважають (а) Світло поширюється (дифрактує) з кожної щілини, оскільки щілини вузькі. Ці хвилі перекриваються і заважають конструктивно (яскраві лінії) і руйнівно (темні області). Ми можемо побачити це лише в тому випадку, якщо світло падає на екран і розсіюється в наші очі. (b) Схема перешкод з подвійною щілиною для водних хвиль майже ідентична малюнку для світла. Хвильова дія найбільша в регіонах конструктивного втручання і найменше в регіонах руйнівного втручання. (c) Коли світло, що пройшло через подвійні щілини, падає на екран, ми бачимо такий візерунок.

    зображення

    Теоретична конструктивна та деструктивна хвильова інтерференція: Амплітуди хвиль складаються разом. (а) Чисті конструктивні перешкоди отримують, коли однакові хвилі знаходяться у фазі. (b) Чисті руйнівні перешкоди виникають, коли однакові хвилі точно поза фазою (зміщені на половину довжини хвилі).

    Візерунок, що виникає в результаті подвійної щілинної дифракції, не є випадковим, хоча може здатися таким чином. Кожна щілина - це різна відстань від заданої точки на стіні за нею. Для кожної різної відстані різна кількість довжин хвиль вписується в цей шлях. Хвилі все починаються у фазі (відповідність гребеня до гребеня), але залежно від відстані точки на стіні від щілини, вони можуть перебувати у фазі в цій точці і конструктивно втручатися, або вони можуть вийти з фази і заважати один одному руйнівно.

    Дифракційні решітки: X-Ray, решітка, відображення

    Дифракційна решітка має періодичну структуру, яка розщеплює і дифрактує світло на кілька променів, що рухаються в різних напрямках.

    цілі навчання

    • Опишіть функцію дифракційної решітки

    Дифракційна решітка

    Дифракційна решітка - це оптична складова з періодичною структурою, яка розщеплює і дифрактує світло на кілька пучків, що рухаються в різних напрямках. Напрямки цих променів залежать від відстані решітки та довжини хвилі світла, так що решітка виступає в якості дисперсійного елемента. Через це решітки часто використовуються в монохроматорах, спектрометрах, пристроях мультиплексування з поділом довжини хвилі, пристроях для стиснення оптичних імпульсів та багатьох інших оптичних приладах.

    Фотографічний слайд з дрібним малюнком фіолетових ліній утворює складну решітку. Для практичного застосування решітки, як правило, мають гребені або постанови на своїй поверхні, а не темні лінії. Такі решітки можуть бути як пропускаючими, так і світловідбиваючими. Решітки, які модулюють фазу, а не амплітуду падаючого світла, також виробляються, часто використовуючи голографію.

    Звичайні пресовані CD і DVD носії є повсякденними прикладами дифракційних решіток і можуть бути використані для демонстрації ефекту, відбиваючи сонячне світло від них на білу стіну. (Див.). Це побічний ефект їх виготовлення, оскільки одна поверхня компакт-диска має багато невеликих ям у пластиці, розташованих по спіралі; ця поверхня має тонкий шар металу, нанесений, щоб зробити ями більш помітними. Структура DVD оптично схожа, хоча може мати більше однієї поверхні без кісточок, а всі поверхні без кісточок знаходяться всередині диска. У стандартній пресованій вініловій платівці при погляді з низького кута, перпендикулярного канавок, можна побачити подібний, але менш певний ефект, ніж у CD/DVD. Це пов'язано з кутом огляду (меншим, ніж критичний кут відбиття чорного вінілу) та траєкторією світла, що відбивається через зміни канавками, залишаючи позаду райдужний рельєфний малюнок.

    зображення

    Зчитувана поверхня компакт-диска: Зчитувана поверхня компакт-диска включає спіральну доріжку, намотану досить щільно, щоб змусити світло дифракціюватися в повний видимий спектр.

    Деякі пташині пір'я використовують природні дифракційні решітки, які створюють конструктивні перешкоди, надаючи пір'ям райдужний ефект. Райдужність - це ефект, коли поверхні, здається, змінюють колір при зміні кута освітлення. Опал - ще один приклад дифракційної решітки, яка відображає світло в різні кольори.

    Рентгенівська дифракція

    Рентгенівська кристалографія - це метод визначення атомної і молекулярної структури кристала, при якому кристалічні атоми змушують пучок рентгенівських променів дифракціюватися в багатьох специфічних напрямках. Вимірюючи кути і інтенсивності цих дифрагованих пучків, кристалограф може скласти тривимірну картину щільності електронів всередині кристала. З цієї електронної щільності можна визначити середні положення атомів в кристалі, а також їх хімічні зв'язки, їх розлад і різну іншу інформацію.

    При рентгенівському вимірі дифракції кристал встановлюється на кутометрі і поступово обертається під час бомбардування рентгенівськими променями, створюючи дифракційну картину регулярно розташованих плям, відомих як відбиття (див.). Двовимірні зображення, зроблені при різних обертаннях, перетворюються в тривимірну модель щільності електронів всередині кристала за допомогою математичного методу перетворень Фур'є, поєднану з хімічними даними, відомими для зразка.

    зображення

    Відбиття в дифракційних візерунках: Кожна точка, яка називається відображенням, у цій дифракційній схемі утворюється від конструктивної інтерференції розсіяних рентгенівських променів, що проходять через кристал. Дані можуть бути використані для визначення кристалічної структури.

    Одинарна щілинна дифракція

    Однощілинна дифракція - це явище, яке виникає при проходженні хвиль через вузьку щілину і згинаються, утворюючи інтерференційну картину.

    цілі навчання

    • Сформулюйте принцип Гюйгенса

    Дифракція

    Як ми пояснювали в попередньому атомі, дифракція визначається як вигин хвилі навколо країв отвору або перешкоди. Дифракція - це явище, яке можуть відчувати всі типи хвиль. Це пояснюється принципом Гюйгенса-Френеля та принципом суперпозиції хвиль. Перший стверджує, що кожна точка на хвильовому фронті є джерелом хвилетів. Ці вейвлети поширюються в прямому напрямку, з тією ж швидкістю, що і вихідна хвиля. Новий хвильовий фронт є лінією дотичною до всіх хвилетів. Принцип суперпозиції стверджує, що в будь-якій точці, чистий результат множинних подразників - це сума всіх подразників.

    Одинарна щілинна дифракція

    При однощілинної дифракції дифракційна картина визначається довжиною хвилі і довжиною щілини. На малюнку 1 показана візуалізація цього візерунка. Це найбільш спрощений спосіб використання принципу Гюйгенса-Френеля, який був покритий попереднім атомом, і застосування його для щілинної дифракції. Але що відбувається, коли щілина НЕ є точною (або близькою до точної) довжини однієї хвилі?

    зображення

    Однощілинна дифракція - одна довжина хвилі: Візуалізація дифракції однієї щілини, коли щілина дорівнює одній довжині хвилі.

    Щілина, яка ширша за одну хвилю, буде виробляти інтерференційні ефекти нижче за течією від щілини. Це легше зрозуміти, думаючи про щілину не як про довгу щілину, а як ряд точкових джерел, розташованих рівномірно по ширині щілини. Це можна побачити на малюнку 2.

    зображення

    Однощілинна дифракція - Чотири довжини хвиль: Цей малюнок показує одну щілинну дифракцію, але щілина - це довжина 4 довжини хвиль.

    Щоб краще вивчити цей ефект, розглянемо одну монохроматичну довжину хвилі. Це призведе до отримання хвильового фронту, який знаходиться в одній фазі. Нижче за течією від щілини світло в будь-якій заданій точці складається з внесків кожного з цих точкових джерел. Отримані фазові відмінності викликані різною довжиною шляху, що сприяють порції променів пройшли з щілини.

    Зміна інтенсивності хвилі може бути математично змодельована. Від центру щілини дифракційні хвилі поширюються радіально. Кут мінімальної інтенсивності (θ min) може бути пов'язаний з довжиною хвилі (λ) та шириною щілини (d) таким чином, що:

    \[\mathrm { d } \sin \theta _ { \min } = \lambda\]

    Інтенсивність (I) хвиль під будь-яким кутом також може бути розрахована як відношення до ширини щілини, довжини хвилі та інтенсивності вихідних хвиль перед проходженням через щілину:

    \[\mathrm { I } ( \theta ) = \mathrm { I } _ { 0 } \left( \dfrac { \sin ( \pi \mathrm { x } ) } { \pi \mathrm { x } } \right) ^ { 2 }\]

    де x дорівнює:

    \[\dfrac { \mathrm { d } } { \lambda } \sin \theta\]

    Критерій Релея

    Критерій Релея визначає кут відриву між двома джерелами світла, які відрізняються один від одного.

    цілі навчання

    • Поясніть значення критерію Релея

    Обмеження дозволу

    Поряд з дифракційними ефектами, які ми обговорювали в попередніх атомах, дифракція також обмежує деталі, які ми можемо отримати на зображеннях. показує три різні обставини межі роздільної здатності через дифракцію:

    зображення

    Межі роздільної здатності: (a) Монохроматичне світло, що проходить через невелику кругову діафрагму, створює цю дифракційну картину. (b) Два точкових джерела світла, близькі один до одного, створюють зображення, що перекриваються через дифракцію. (c) Якщо вони ближче один до одного, їх неможливо вирішити або розрізнити.

    • (а) показує світло, що проходить через невелику кругову діафрагму. Ви бачите не різкий круговий контур, а пляма з нечіткими краями. Це пов'язано з дифракцією, подібною до такої через єдину щілину.
    • (б) показує два точкових джерела близько один до одного, створюючи зображення, що перекриваються. Завдяки дифракції можна просто ледве розрізнити два точкових джерела.
    • (c) показує два точкових джерела, які так близько один до одного, що ви більше не можете розрізнити їх.

    Цей ефект можна побачити при світлі, що проходить через невеликі отвори або більші отвори. Цей же ефект відбувається, коли світло проходить через наші зіниці, і саме тому людське око має обмежену гостроту.

    Критерій Релея

    У 19 столітті лорд Релі винайшов критерій визначення того, коли два джерела світла були помітні один від одного, або дозволені. Згідно з критеріями, два точкових джерела вважаються просто вирішеними (досить помітними один від одного, щоб розпізнати два джерела), якщо центр дифракційної картини одного безпосередньо перекривається першим мінімумом дифракційної картини іншого. Якщо відстань між цими точками більше, джерела добре вирішуються (тобто їх легко відрізнити один від одного). Якщо відстань менше, вони не вирішуються (тобто їх неможливо відрізнити один від одного). Рівняння для визначення цього є:

    \[\theta = 1.22 \dfrac { \lambda } { \mathrm { D } }\]

    θ — кут, на який об'єкти розділені, в радіані λ — довжина хвилі світла D — діаметр діафрагми. показує це поняття візуально. Це рівняння також дає кутове поширення джерела світла, що має діаметр D.

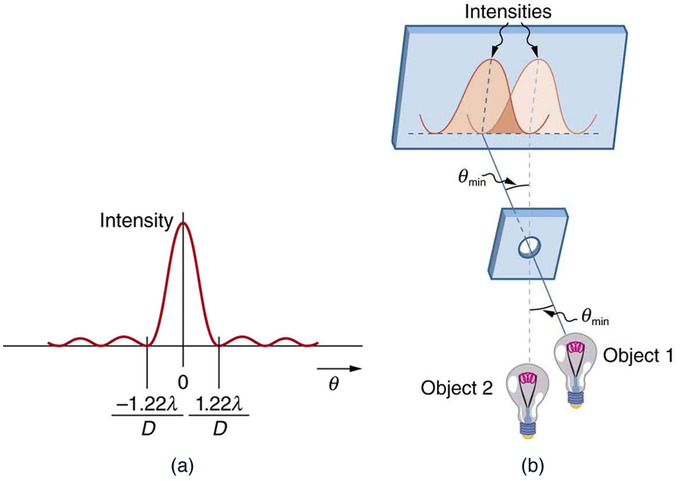
    зображення

    Критерій Релея: (а) Це графік інтенсивності дифракційної картини для кругової діафрагми. Відзначимо, що, подібно до однієї щілини, центральний максимум ширше і яскравіше, ніж у боків. (b) Два точкові об'єкти створюють перекриваються дифракційні візерунки. Тут показаний критерій Релея для того, щоб бути просто розв'язним. Центральний максимум одного візерунка лежить на першому мінімумі іншого.

    Ключові моменти

    • Дифракція - це поняття, яке пояснюється за допомогою принципу Гюйгенса, і визначається як вигин хвилі навколо країв отвору або перешкоди.
    • Цей принцип можна використовувати для визначення відображення, як показано на малюнку. Він також може бути використаний для пояснення заломлення та перешкод. Все, що відчуває це явище, - хвиля. Застосовуючи цю теорію до світла, що проходить через щілину, ми можемо довести, що це хвиля.
    • Принцип можна показати за допомогою рівняння нижче: s=vt s — відстань v — швидкість розповсюдження t — час Кожна точка на хвильовому фронті випромінює хвилю зі швидкістю, v. Випромінювані хвилі напівкруглі і відбуваються в t, час пізніше. Новий хвильовий фронт дотичний до хвилетів.
    • Хвильові характеристики світла змушують світло проходити крізь щілини і заважати один одному, створюючи світлі та темні ділянки на стіні за щілинами. Світло, що з'являється на стіні за щілинами, частково поглинається стіною, характерною для частинки.
    • Конструктивне втручання виникає, коли хвилі заважають один одному від гребеня до гребеня і хвилі точно перебувають у фазі один з одним. Руйнівні перешкоди виникають, коли хвилі заважають один одному від гребеня до корита (пік-долина) і точно поза фазою один з одним.
    • Кожна точка на стіні має різну відстань до кожної щілини; різна кількість довжин хвиль вписується в ці два шляхи. Якщо дві довжини шляху відрізняються на половину довжини хвилі, хвилі будуть заважати руйнівно. Якщо довжина шляху відрізняється на цілу довжину хвилі, хвилі заважають конструктивно.
    • Напрямки дифрагованих променів залежать від відстані решітки та довжини хвилі світла, так що решітка виступає в якості дисперсійного елемента.
    • Решітки зазвичай використовуються в монохроматорах, спектрометрах, пристроях мультиплексування з поділом довжини хвилі, оптичних імпульсних стискаючих пристроях та інших оптичних приладах.
    • Дифракція рентгенівського випромінювання використовується в кристалографії для отримання тривимірної картини щільності електронів всередині кристала.
    • Принцип Гюйгенса стверджує, що кожна точка на хвильовому фронті є джерелом хвилетів. Ці вейвлети поширюються в прямому напрямку, з тією ж швидкістю, що і вихідна хвиля. Новий хвильовий фронт є лінією дотичною до всіх хвилетів.
    • Якщо щілина довша за одну довжину хвилі, подумайте про неї як про ряд точкових джерел, розташованих рівномірно по ширині щілини.
    • Нижче за течією від щілини, яка довша за одну довжину хвилі, світло в будь-якій заданій точці складається з внесків кожного з цих точкових джерел. Отримані фазові відмінності викликані різною довжиною шляху, що сприяють порції променів пройшли з щілини.
    • Дифракція відіграє велику роль у роздільній здатності, при якій ми можемо бачити речі. Є момент, коли два джерела світла можуть бути настільки близько один до одного, що ми не можемо їх розрізнити.
    • Коли два джерела світла знаходяться близько один до одного, вони можуть бути: невирішеними (тобто не здатними відрізнити одне від іншого), просто дозволеними (тобто здатні лише відрізнити їх окремо один від одного), і трохи добре вирішеними (тобто легко відрізнити один від одного).
    • Для того, щоб два джерела світла були просто вирішені, центр однієї дифракційної картини повинен безпосередньо перекриватися з першим мінімумом іншої дифракційної картини.

    Ключові умови

    • дифракція: вигин хвилі навколо країв отвору або перешкоди.
    • конструктивне втручання: Відбувається, коли хвилі заважають один одному гребінь гребеня і хвилі точно перебувають у фазі один з одним.
    • деструктивні втручання: виникає, коли хвилі заважають один одному гребінь до корита (пік до долини) і точно поза фазою один з одним.
    • перешкоди: Ефект, спричинений накладенням двох систем хвиль, наприклад, спотворення на широкомовному сигналі через атмосферні чи інші ефекти.
    • райдужності: стан або стан переливається; виставка кольорів, подібних до веселки; призматична гра кольору.
    • дифракція: вигин хвилі навколо країв отвору або перешкоди.
    • монохроматичний: описує промінь світла з однією довжиною хвилі (тобто одного конкретного кольору або частоти).
    • роздільна здатність: ступінь тонкості, з якою зображення може бути записано або отримано, часто виражається як кількість пікселів на одиницю довжини (зазвичай дюйм).

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ