9.2: Кутовий момент

Ще в главі 3 ми ввели імпульс об'єкта, що рухається в одному вимірі\(p = mv\), і виявили, що він має цікаву властивість зберігатися при зіткненнях між об'єктами, що складають ізольовану систему. Здається закономірним запитати, чи має відповідна величина обертання, утворена множенням «обертальної інерції»\(I\) та кутової швидкості\(\omega\), якісь цікаві властивості. Ми орієнтовно ¹ будемо називати величину\(I\omega\) кутового моменту (щоб відрізнити його від «звичайного» або лінійного імпульсу,\(mv\)), і будувати до кращого розуміння та формального визначення його, в решті частини цього розділу.

Незабаром очевидні дві речі: одна полягає в тому, що, на відміну від обертальної кінетичної енергії, яка була просто звичайною кінетичною енергією, кількість\(I\omega\) дійсно відрізняється від звичайного імпульсу, оскільки вона має різні розміри (див. «додатковий» коефіцієнт\(R\) у Рівнянні (\ ref {eq:9.4}) нижче). Інша полягає в тому, що насправді існують системи в природі, де ця величина, здається, залишається постійною до хорошого наближення. Наприклад, Земля, що обертається навколо своєї осі, з постійною швидкістю\(2\pi\) радіанів кожні 24 години, має, в силу цього, постійний кутовий імпульс (постійний\(I\) і\(\omega\)).

Найкраще, однак, почати з думки про те, як ми б визначити «кутовий момент» для системи, що складається з однієї частинки, а потім нарощування звідти, як ми робили весь семестр з кожною новою концепцією. Для частинки, що рухається по колу, згідно з попереднім розділом, момент інерції справедливий\(I = mR^2\), а тому\(I\omega\) справедливий\(mR^2\omega\). Використовуючи Equation (8.4.12), ми можемо писати (буква\(L\) є умовним символом для кутового моменту; не помилитеся з його довжиною!)

\[ L=I \omega=\pm m R|v| \quad \mathrm{ (particle \: moving \: in \: a \: circle) } \label{eq:9.4} \]

де, для узгодженості з нашим знаком конвенції для\(\omega\), ми повинні використовувати позитивний знак, якщо обертання проти годинникової стрілки, і негативний знак, якщо він за годинниковою стрілкою.

Ми знову можемо легко думати про приклади в природі, де кількість (\ ref {eq:9.4}) зберігається: наприклад, Місяць, якщо розглядати її як частинку, що обертається навколо Землі приблизно по круговій орбіті ², має тоді приблизно постійний кутовий імпульс, як це задано рівнянням (\ ref {eq:9.4}). Цей приклад цікавий ще й тим, що він пропонує уявлення про важливу різницю між звичайним імпульсом та кутовим: виявляється, що останній може бути збережений навіть при наявності деяких видів зовнішніх сил (в даному випадку, сили тяжіння завдяки Землі, яка утримує Місяць на його орбіта).

З іншого боку, не відразу видно, як узагальнити визначення (9.4) до інших видів руху. Якщо ми просто спробуємо щось на зразок\(L = mvr\), де\(r\) відстань до нерухомої осі, або до нерухомої точки, то виявимо, що це дає величину, яка постійно змінюється, навіть для найпростішої можливої фізичної системи, а саме частинки, що рухається по прямій з постійною швидкістю. Тим не менш, ми хотіли б визначити\(L\) таким чином, що вона залишатиметься постійною, коли насправді нічого в реальному стані руху частинки не змінюється.

Спосіб зробити це для частинки, що рухається по прямій лінії, полягає у визначенні\(L\) як добутку\(mv\) часу, а не відстань частинки до точки, а відстань лінії руху частинки до розглянутої точки. «Лінія руху» - це просто пряма лінія, яка містить вектор швидкості в будь-який момент часу. Відстань між прямою і точкою О є, за визначенням, найкоротшою відстанню від O до будь-якої точки на прямій; вона задається довжиною відрізка, проведеного перпендикулярно прямій через точку О.

Для частинки, що рухається по колу, лінія руху в будь-який час є дотичною до кола, і тому відстань між лінією руху і центром кола є лише радіусом\(R\), тому ми відновлюємо визначення Рівняння (\ ref {eq:9.4}). Для загального випадку, з іншого боку, у нас є ситуація, показана на малюнку\(\PageIndex{1}\): якщо миттєва швидкість частинки є\(\vec v\), і ми малюємо вектор положення частинки\(\vec r\), з точкою O як початок, то відстань між O і лінією руху (іноді також називається перпендикулярна відстань між O і частинкою) задається\(r \sin \theta\) тим, де\(\theta\) знаходиться кут між векторами\(\vec r\) і\(\vec v\).

Малюнок\(\PageIndex{1}\): Для частинки, що рухається по прямій, відстань від точки О до лінії руху частинки (пунктирна лінія) дорівнює в кожній\(r \sin \theta\) точці траєкторії (дві можливі точки показані на малюнку). Відстань - довжина синього відрізка. На малюнку показано, що існує певна свобода у виборі того, як\(\vec v\) вимірюється кут\(\theta\) між\(\vec r\) і повинен бути\(\theta\) виміряний, оскільки синус такого ж, як синус\(\pi - \theta\).

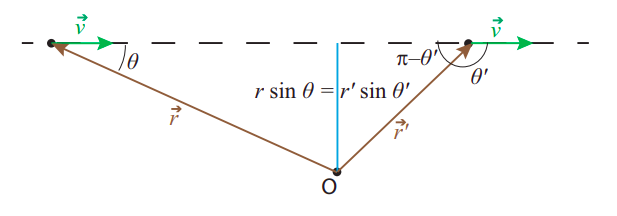
Тому ми намагаємося визначити кутовий імпульс відносно точки O як продукт.

\[ L=\pm m r|v| \sin \theta \label{eq:9.5} \]

з позитивним знаком, якщо точка О знаходиться зліва від лінії руху, коли частинка проходить повз (що відповідає руху проти годинникової стрілки по колу), і негативним в іншому випадку.

Є дві дуже хороші речі щодо визначення (\ ref {eq:9.5}): перша полягає в тому, що вже існує математична операція між векторами, яка називається вектором, або перехресним, добутком, згідно з якою\(|L|\), як визначено (\ ref {eq:9.5}), буде просто бути дано\(|\vec{r} \times \vec{p}| \), де\(\vec{r} \times \vec{p} \) перехресний добуток\(\vec r\) і\(\vec p\); Я буду мати набагато більше сказати про це в наступному підрозділі. Друга хороша річ полягає в тому, що при такому визначенні кутовий імпульс буде збережений у важливому виді процесу, а саме зіткненні, яке перетворює лінійний в обертальний рух, як показано на малюнку\(\PageIndex{2}\) нижче.

Малюнок\(\PageIndex{2}\): Зіткнення між двома частинками, 1 і 2, рівних мас. Частинка 2 прив'язується безмасовою струною до точки О. Після зіткнення частка 1 знаходиться в стані спокою і частка 2 рухається по зображеному колу.

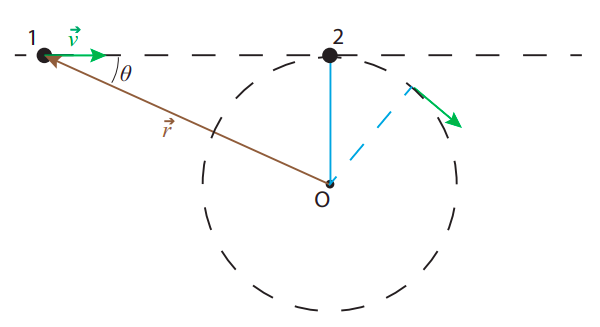
На зображенні частка 1 спочатку рухається з постійною швидкістю\(\vec v\) і частка 2 спочатку знаходиться в стані спокою, прив'язаною безмасовою струною до точки О. Якщо частинки мають однакову масу, збереження (звичайного) імпульсу і кінетичної енергії означає, що при зіткненні вони обмінюються швидкостями: частка 1 зупиняється і частка 2 починає рухатися вправо з тією ж швидкістю v, але відразу струна починає тягнути за неї і згинати свій шлях в коло. Припускаючи незначне тертя між струною та поворотною точкою (і всіма задіяними поверхнями), швидкість частинки 2 залишатиметься постійною, коли вона обертається, зберігаючи кінетичну енергію, оскільки напруга в струні завжди перпендикулярно вектору переміщення частинки, тому це не працює на ньому.

Все вищесказане означає, що кутовий імпульс зберігається: до зіткнення він дорівнював\(−mvr \sin \theta = −mvR\) для частинки 1, а 0 для частинки 2; після зіткнення він дорівнює нулю для частинки 1 і\(I\omega = mR^2\omega = −mRv\) для частинки 2 (примітка\(\omega\) негативна, тому що обертання відбувається за годинниковою стрілкою). Кінетична енергія також зберігається, з причин, аргументованих вище. З іншого боку, звичайний імпульс зберігається лише лише після зіткнення, коли струна починає тягнути частку 2, оскільки це являє собою зовнішню силу на систему.

Отже, ми знайшли ситуацію, в якій лінійний рух перетворюється на круговий рух, тоді як кутовий момент, як визначено Equation (\ ref {eq:9.5}), зберігається, і це незважаючи на наявність зовнішньої сили. Це правда, що насправді ми змогли вирішити остаточний рух, не використовуючи явного збереження кутового моменту: нам потрібно було лише викликати збереження звичайного імпульсу протягом короткого часу зіткнення та збереження кінетичної енергії. Але легко узагальнити задачу, зображену на малюнку,\(\PageIndex{2}\) до тієї, яка не може бути вирішена цими методами, але може бути вирішена, якщо кутовий імпульс постійний. Припустимо, що ми замінюємо частку 2 і струну тонким стрижнем маси\(m\) і довжини, що\(l\) обертається на одному кінці. Що відбувається зараз, коли частка 1 б'є стрижень?

Малюнок\(\PageIndex{3}\): Зіткнення між частинкою, яка спочатку рухається зі швидкістю,\(\vec v_1\) і стрижнем довжини\(l\), що обертається в кінцевій точці. Частинка б'є стрижень перпендикулярно, на іншому кінці. Після зіткнення частка рухається по одній лінії зі швидкістю\(\vec v_f\), а стрижень обертається навколо точки О з кутовою швидкістю\(\omega\).

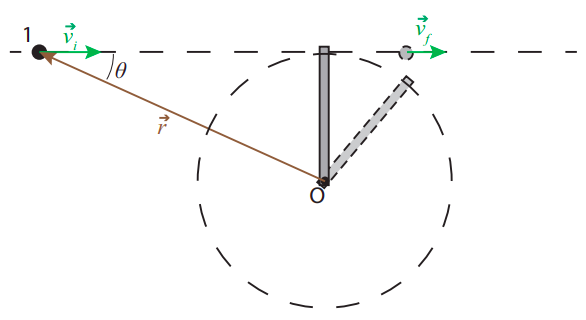
Якщо частка вражає стрижень перпендикулярно, і зіткнення відбувається дуже швидко (тобто воно закінчилося до того, як стрижень встигне рухатися на значну відстань), ми можемо припустити, що сила, що чиниться стрижнем на частку (нормальна сила), знаходиться уздовж початкової лінії руху, тому частка буде продовжувати рухатися на цій лінії. З іншого боку, цього разу ми не можемо нехтувати силою, яку надає стрижень на штангу під час зіткнення, оскільки планка є одним жорстким предметом. Це означає, що система не ізольована під час зіткнення, і ми не можемо розраховувати на звичайне збереження імпульсу.

Припустимо, однак, що кутовий імпульс\(L\) зберігається, а також загальна енергія (стрижень не працює на системі, так як немає зміщення цієї точки). Початковий момент імпульсу дорівнює\(L_i = −mv_il\). Кінцевий момент моменту -\(−mv_{f}l\) для частинки (зверніть увагу, що, якщо частка відскакує назад,\(v_f\) буде негативним) і\(I\omega\) для стрижня. Початкова кінетична енергія є\(K_i = \frac{1}{2}mv^2_i\), а кінцева кінетична енергія -\(\frac{1}{2}mv^2_f\)\(\frac{1}{2}I\omega ^2\) для частинки і для стрижня (відгук Рівняння (9.1.2), тому ми повинні вирішити систему

\ begin {вирівнювання}
-м v_ {i} l &=-м v_ {f} l+I\ омега\
\ nonumber\\ frac {1} {2} м v_ {i} ^ {2} &=\ frac {1} {2} m v_ {f} ^ {2} +\ frac {1} {2} I\ омега^ {2} :9.6}
\ end {вирівнювання}

Загальним рішенням для довільних значень всіх констант є

\ begin {вирівнювання}
v_ {f} &=\ розрив {м l^ {2} -I} {м l^ {2} +I} v_ {i}\ nonumber\
\ омега&=-\ розрив {2 м л} {м l^ {2} +I} v_ {i}\ мітка {еква:9.7}
\ кінець {вирівнювання}

Зверніть увагу, що це зменшується до наших попередніх результатів для зіткнення двох частинок, якщо ми зробимо\(I = ml^2\) (що завжди можна було зробити, вибравши масу стрижня\(M\), відповідним чином). З іншого боку, як зазначено в кінці попереднього підрозділу, для загального\(M\) ми маємо\(I = \frac{1}{3}Ml^2\) для стрижня, тому ми можемо скасувати\(l^2\) майже скрізь і закінчити

\ begin {вирівнювання}
v_ {f} &=\ розрив {3 м-м} {3 м+м} v_ {i}\ nonumber\
\ омега &=-\ розрив {6 м} {3 м+м}\ розрив {v_ {i}} {l}\ етикетка {eq:9.8}
\ кінець {вирівнювання}

Зокрема, ми бачимо, що якщо\(m = M\) частинка продовжує рухатися вперед з 1/2 своєї початкової швидкості, і стрижень обертається з\(\omega = −(3/2)v_i/l\), що насправді є більшою кутовою швидкістю, ніж те, що ми знайшли для системи на малюнку\(\PageIndex{2}\).

Цей приклад показує, наскільки корисним може бути збереження кутового моменту, але, звичайно, ми ще не знаємо, чи дійсно кутовий імпульс зберігається в цій проблемі! Я вирішу це дуже важливе питання - коли зберігається момент імпульсу - у розділі після наступного, тобто після того, як я належним чином розробив кутовий імпульс як векторну величину.

---

¹ Як ми побачимо нижче, в цілому\(I\omega\) дорівнює лише одній складовій вектора моменту моменту.

² Ви можете заглянути вперед на рис. 10.1.1, у наступному розділі, щоб побачити, наскільки добре це може бути наближення!