9.3: Перехресний продукт і обертальні величини
- Page ID
- 74578
Хрест, або вектор, добуток двох векторів\(\vec A\) і\(\vec B\) позначається\(\vec{A} \times \vec{B}\). Він визначається як вектор, перпендикулярний обом\(\vec A\) і\(\vec B\) (тобто площині, яка містить їх обох), з величиною, заданою
\[ |\vec{A} \times \vec{B}|=A B \sin \theta \label{eq:9.9} \]
де\(A\) і\(B\) - величини\(\vec A\) і\(\vec B\), відповідно, і\(\theta\) - кут між\(\vec A\) і\(\vec B\), коли вони намальовані або з однаковим походженням, або від кінчика до хвоста.
Конкретний напрямок\(\vec A \times \vec B\) залежить від відносної орієнтації двох векторів. В основному, якщо\(\vec B\) проти годинникової стрілки від\(\vec A\), коли дивиться вниз на площину, в якій вони лежать, припускаючи, що вони намальовані із загальним походженням, то\(\vec{A} \times \vec{B}\) вказує вгору від цієї площини; інакше вона вказує вниз (в площину). Можна також використовувати так зване правило правої руки, проілюстроване\(\PageIndex{1}\) на малюнку, щоб з'ясувати напрямок\(\vec{A} \times \vec{B}\). Відзначимо, що за цим визначенням напрямок\(\vec{A} \times \vec{B}\) є протилежним напрямку\(\vec{B} \times \vec{A}\) (як це також показано на малюнку\(\PageIndex{1}\)). Отже, крос-продукт є некомутативним: порядок факторів має значення.
\[ \vec{A} \times \vec{B}=-\vec{B} \times \vec{A} \label{eq:9.10} \]
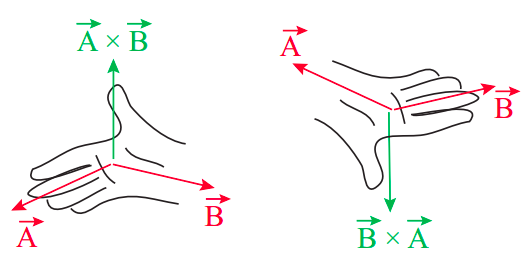
З Equation (\ ref {eq:9.10}) випливає, що перехресний добуток будь-якого вектора з самим собою повинен дорівнювати нулю. Насправді, згідно з Equation (\ ref {eq:9.9}), перехресний добуток будь-яких двох векторів, паралельних один одному, дорівнює нулю, оскільки в цьому випадку\(\theta\) = 0, і\(\sin 0\) = 0. У цьому відношенні перехресний добуток протилежний точковому добутку, який ми ввели в главі 7: це максимум, коли вектори, що множаться, ортогональні, і нуль, коли вони паралельні. (І, звичайно, результат\(\vec{A} \times \vec{B}\) - вектор, тоді як\(\vec{A} \cdot \vec{B}\) скалярний.)
Крім того, що не комутативний, перехресний твір також не має асоціативної властивості звичайного множення:\(\vec{A} \times(\vec{B} \times \vec{C}) \) відрізняється від\((\vec{A} \times \vec{B}) \times \vec{C} \). Ви можете легко переконатися в цьому з того, що, якщо\(\vec A = \vec B\), другий вираз буде нульовим, а ось перше взагалі буде ненульовим (так як\(\vec{A} \times \vec{C}\) не паралельно, а скоріше перпендикулярно\(\vec A\)).
Незважаючи на ці дивацтва, крос-твір надзвичайно корисний у фізиці. Ми будемо використовувати його для визначення\(\vec L\) вектора кутового моменту частинки, відносно точки O, наступним чином:
\[ \vec{L}=\vec{r} \times \vec{p}=m \vec{r} \times \vec{v} \label{eq:9.11} \]
де\(\vec r\) - вектор положення частинки, щодо точки О. Це визначення дає нам постійний вектор для частинки, що рухається по прямій лінії, як обговорювалося в попередньому розділі: величина\(\vec L\), згідно з рівнянням (\ ref {eq:9.9}) буде\(mrv \sin \theta\), яка, як показано на Малюнок 9.2.1, не змінюється в міру руху частинки. Що стосується напрямку, то воно завжди перпендикулярно площині, що містить\(\vec r\) і\(\vec v\) (площину паперу, на рис. 9.2.1), і якщо ви уявляєте собі переміщення\(\vec v\) в точку О, тримаючи її паралельно собі, і застосуєте правило правої руки, ви побачите, що\(\vec L\) в Малюнок 9.2.1, повинен завжди вказувати в площину паперу.
Щоб побачити, як працює визначення (\ ref {eq:9.11}) для частинки, що рухається по колу, знову розглянемо ситуацію, показану на малюнку 8.4.2 в попередньому розділі, але тепер розширити її до трьох вимірів, як на малюнку\(\PageIndex{2}\), на наступній сторінці. Легко перевірити, що для показаного напрямку руху поперечний продукт завжди\(\vec{r} \times \vec{v}\) буде спрямований вгору, вздовж позитивної\(z\) осі. Крім того, оскільки\(\vec r\) і\(\vec v\) завжди залишатися перпендикулярними, величина\(\vec L\), за рівнянням (\ ref {eq:9.9}) завжди\(|\vec{L}|=m R|\vec{v}|\) буде.Беручи до уваги\(I = mR^2\) і Рівняння (8.4.12), ми бачимо, що ми маємо тоді
\[ |\vec{L}|=\left(m R^{2}\right) \frac{|\vec{v}|}{R}=I|\omega| \label{eq:9.12} \]
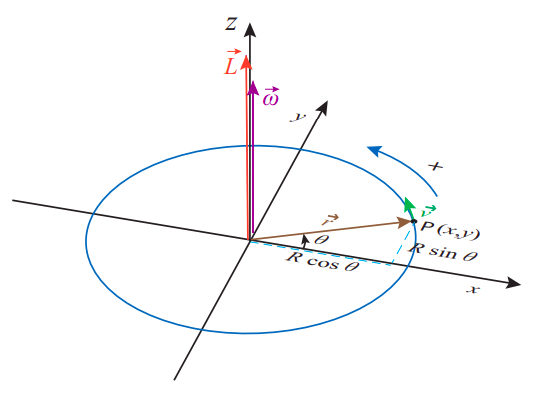
Це говорить про те, що ми повинні визначити вектор кутової швидкості\(\vec \omega\), як вектор величини\(|\omega|\), спрямований вздовж позитивної\(z\) осі, якщо рух у\(y\) площині\(x\) - проти годинникової стрілки, як видно зверху (і в протилежному напрямку інакше). Тоді це буде триматися як векторне рівняння:
\[ \vec{L}=I \vec{\omega} \label{eq:9.13} .\]
Може здатися дуже дивним вибором мати кутову точку швидкості вздовж\(z\) осі, коли частка рухається в\(y\) площині\(x\) -, але певним чином це має сенс. Припустимо, частинка рухається з постійною кутовою швидкістю: напрямки\(\vec r\) і постійно\(\vec v\) змінюються, але\(\vec \omega\) спрямовані вздовж позитивного\(z\) напрямку, яке залишається фіксованим протягом усього
Є деякі інші акуратні речі, які ми можемо зробити\(\vec \omega\), як визначено вище. Розглянемо перехресний виріб\(\vec{\omega} \times \vec{r}\). Огляд малюнка\(\PageIndex{2}\) та рівняння (8.4.12) показує, що це не що інше, як звичайний вектор швидкості\(\vec v\):
\[ \vec{v}=\vec{\omega} \times \vec{r} \label{eq:9.14} .\]
Ми також можемо взяти похідну\(\vec \omega\) для отримання вектора кутового прискорення\(\vec \alpha\), так що рівняння (8.4.9) буде триматися як векторне рівняння:
\[ \vec{\alpha}=\lim _{\Delta t \rightarrow 0} \frac{\vec{\omega}(t+\Delta t)-\vec{\omega}(t)}{d t}=\frac{d \vec{\omega}}{d t} \label{eq:9.15} .\]
Для руху, зображеного на малюнку\(\PageIndex{2}\), вектор\(\vec \alpha\) буде вказувати уздовж позитивної\(z\) осі, якщо вектор зростає (\(\vec \omega\)це означає, що частка прискорюється), і вздовж негативної\(z\) осі, якщо\(\vec \omega\) зменшується.
Однією з важливих властивостей, якими володіє перехресний добуток, є розподільна властивість щодо суми:
\[ (\vec{A}+\vec{B}) \times \vec{C}=\vec{A} \times \vec{C}+\vec{B} \times \vec{C} \label{eq:9.16} .\]
Це, виявляється, все, що потрібно для того, щоб мати можливість застосувати правило добутку диференціації для обчислення похідної від перехресного добутку; ви просто повинні бути обережними, щоб не змінювати порядок факторів при цьому. Потім ми можемо взяти похідну обох сторін рівняння (\ ref {eq:9.14}), щоб отримати вираз для вектора прискорення:
\ почати {вирівняти}
\ vec {a} =\ frac {d\ vec {v}} {d t} &=\ розрив {d\ vec {\ омега}} {d t}\ час\ vec {r} +\ vec {\ омега}\ час {d\ vec {r}} {d t}\ nonumber\
&=\ vec {альфа}\ час {d\ vec {r} r} +\ vec {\ омега}\ раз\ vec {v}\ етикетка {еква:9.17}.
\ end {вирівняти}
Перший член з правого боку\(\vec{\alpha} \times \vec{r}\), лежить в\(x\) -\(y\) площині, і перпендикулярний\(\vec r\); отже, він є дотичним до кола. Насправді, дивлячись на його величину, зрозуміло, що це всього лише тангенціальний вектор прискорення, який я ввів (як скаляр) в Equation (8.4.13).
Що стосується другого члена в (\ ref {eq:9.17}), зазначивши\(\vec \omega \times \vec v\), що\(\vec \omega\) і завжди\(\vec v\) перпендикулярні, зрозуміло, що його величина є\(|\omega||\vec{v}|=R \omega^{2}=v^{2} / R\) (використовуючи Рівняння (8.4.12) знову). Це якраз величина доцентрового прискорення ми вивчали в попередньому розділі (розділ 8.4). Також, використовуючи правило правої руки на малюнку\(\PageIndex{2}\), ви можете побачити, що\(\vec{\omega} \times \vec{v}\) завжди вказує всередину, до центру кола; тобто вздовж напрямку\(−\vec r\). Поклавши все це разом, ми можемо записати цей вектор як справедливий\(−\omega^2 \vec r\), а весь вектор прискорення як суму тангенціальної та доцентрової (радіальної) складової, наступним чином:
Щоб завершити цей розділ, дозвольте мені повернутися до вектора моменту моменту і задати питання про те, чи задовольнить чи взагалі кутовий момент обертової системи, визначеної як сума рівняння (\ ref {eq:9.11}) над усіма частинками, що складають систему, чи не задовольнить векторне рівняння\(\vec L = I\omega\). Ми бачили, що це дійсно працює для частинки, що рухається по колу. Отже, він також буде працювати для будь-якого об'єкта, який по суті є плоским, і обертається навколо осі, перпендикулярної йому, оскільки в цьому випадку всі його частини просто рухаються колами навколо загального центру. Так було у випадку з тонким стрижнем, який ми розглядали в зв'язку з малюнком 9.2.3 в попередньому підрозділі.
Однак якщо система являє собою тривимірний об'єкт, що обертається навколо довільної осі, результат, як правило,\(\vec L = I\vec \omega\) не тримається. Причина полягає в тому, що математично момент інерції\(I\) визначається (Рівняння (9.1.3)) через відстані частинок до осі, тоді як кутовий момент включає відстань частинки до точки. Для частинок на різній «висоті» по осі обертання ці величини різні. Можна показати, що в загальному випадку все, що ми можемо сказати, це те\(L_z = I\omega_z\), що, якщо ми\(z\) називаємо вісь обертання і обчислимо\(\vec L\) відносно точки на цій осі.
З іншого боку, якщо вісь обертання є віссю симетрії об'єкта, то\(\vec L\) має тільки\(z\) складову, а результат\(\vec L = I\vec \omega\) тримає як векторне рівняння. Більшість систем, які ми розглянемо в цьому семестрі, будуть розглянуті під цим пунктом, або під «по суті плоский» пункт, згаданий вище.
У наступному ми, як правило, припустимо, що\(I\) має лише\(z\) компонент, і ми скинемо індекс\(z\) у рівнянні\(L_z = I\omega_z\), так що\(L\) і не обов'язково\(\omega\) буде величинами відповідних векторів, але числа, які можуть бути позитивними або негативними , В залежності від напрямку обертання (за годинниковою стрілкою або проти годинникової стрілки). Це, по суті, та сама угода, яку ми використовували для векторів в одному вимірі\(\vec p\), наприклад,\(\vec a\) або, на ранніх розділах; це добре для всіх випадків, коли (напрямок) вісь обертання не змінюється з часом, які є єдиними ситуаціями, які ми розглянемо в цьому семестрі.
