8.4: Зв'язані осцилятори

Два з'єднані маятники

Красива демонстрація того, як енергія може передаватися від одного генератора до іншого, забезпечується двома слабо зв'язаними маятниками. Уявімо, що у нас є два однакових маятника довжини\(L\) і маси\(m\), які з'єднані слабкою пружиною з постійною пружини k (рис.\(\PageIndex{1a}\)).

Малюнок\(\PageIndex{1}\): Рух двох спарених маятників. (а) Ескіз установки. Два однакових маятника довжини\(L\) і маси\(m\) з'єднані через слабку пружину постійної пружини\(k\). В якості початкової умови ми вибираємо обидва маятника в спокої, при цьому правий - в положенні рівноваги, а лівий - кінцеву амплітуду. (б) Отриманий рух двох маятників: вліво (синій) і правий (помаранчевий).

Рівняння руху комбінованої системи потім задається:

\[\begin{align} \dot{L} \ddot{\theta}_{1} &=-g \sin \theta_{1}-k L\left(\sin \theta_{1}-\sin \theta_{2}\right) \label{eqofmot1} \\ L \ddot{\theta}_{2} &=-g \sin \theta_{2}+k L\left(\sin \theta_{1}-\sin \theta_{2}\right) \label{eqofmot2} \end{align}\]

Ми ще раз скористаємося невеликим кутовим розширенням, в якому ми можемо наблизити\(\sin \theta \approx \theta\), і ідентифікуємо\(\omega_0 = \sqrt{\frac{g}{L}}\) як частоту кожного з (незв'язаних) маятників. Рівняння\ ref {eqofmot1} і\ ref {eqofmot2} потім стають

\[\begin{align} \ddot{\theta}_1 &=-\omega_{0}^{2} \theta_{1}-k \theta_{1}+k \theta_{2} \label{ddottheta1} \\[4pt] \ddot{\theta}_2 &=-\omega_{0}^{2} \theta_{2}+k \theta_{1}-k \theta_{2} \label{ddottheta2} \end{align}\]

Ми можемо легко розв'язати систему зв'язаних диференціальних рівнянь у рівняннях\ ref {ddottheta1} та\ ref {ddottheta2}, вводячи дві нові змінні:\(\alpha=\theta_{1}+\theta_{2}\) і\(\beta=\theta_{1}-\theta_{2}\), що дає нам два незв'язаних рівняння:

\[\begin{align} \ddot{\alpha} &=-\omega_{0}^{2} \alpha \label{ddotalpha} \\[4pt] \ddot{\beta} &=-\omega_{0}^{2} \beta-2 k \beta=-\left(\omega^{\prime}\right)^{2} \beta \label{ddotbeta} \end{align}\]

де\(\left(\omega^{\prime}\right)^{2}=\omega_{0}^{2}+2 k\) або\(\omega^{\prime}=\sqrt{2 k+g / L}\). Оскільки рівняння\ ref {ddotalpha} і\ ref {ddotbeta} є просто рівняннями гармонічних осциляторів, ми можемо негайно записати їх розв'язки:

\[\begin{align} \alpha(t) &=A \cos \left(\omega_{0} t+\phi_{0}\right) \\ \beta(t) &=B \cos \left(\omega^{\prime} t+\phi^{\prime}\right) \end{align}\]

Перетворення назад до вихідних змінних,\(\theta _1\)\(\theta _2\) а також просто, і дає

\[\begin{align}{\theta_{1}=\frac{1}{2}(\alpha+\beta)=\frac{A}{2} \cos \left(\omega_{0} t+\phi_{0}\right)+\frac{B}{2} \cos \left(\omega^{\prime} t+\phi^{\prime}\right)} \\ {\theta_{2}=\frac{1}{2}(\alpha-\beta)=\frac{A}{2} \cos \left(\omega_{0} t+\phi_{0}\right)-\frac{B}{2} \cos \left(\omega^{\prime} t+\phi^{\prime}\right)}\end{align}\]

Давайте поставимо деякі конкретні початкові умови: ми залишаємо маятник номер 2 в спокої в його рівноважному положенні\((\theta_{2}(0)=\dot{\theta}_{2}(0)=0)\) і даємо маятнику номер 1 кінцеву амплітуду, але також звільняємо його в спокої\((\theta_{1}(0)=\theta_{0}, \dot{\theta}_{1}(0)=0)\). Розробка чотирьох невідомих (\(A, B, \phi_0\)і\(\phi '\)) проста, і ми отримуємо:

\[\begin{align}{\theta_{1}=\frac{\theta_{0}}{2} \cos \left(\omega_{0} t\right)+\frac{\theta_{0}}{2} \cos \left(\omega^{\prime} t\right)=\theta_{0} \cos \left(\frac{\omega_{0}+\omega^{\prime}}{2} t\right) \cos \left(\frac{\omega_{0}-\omega^{\prime}}{2} t\right)} \label{theta1} \\ {\theta_{2}=\frac{\theta_{0}}{2} \cos \left(\omega_{0} t\right)-\frac{\theta_{0}}{2} \cos \left(\omega^{\prime} t\right)=\theta_{0} \sin \left(\frac{\omega_{0}+\omega^{\prime}}{2} t\right) \sin \left(\frac{\omega^{\prime}-\omega_{0}}{2} t\right)} \label{theta2} \end{align}\]

Розв'язок, заданий рівняннями\ ref {theta1} і\ ref {theta2}, побудовано на рисунку\(\PageIndex{1}\). Зверніть увагу, що рішення мають дві частоти (відомі як власні частоти системи). Швидка\(\frac{1}{2}\left(\omega_{0}+\omega^{\prime}\right)\), яка для слабкої константи зчеплення\(k\) дуже близька до \(\omega_0\)власноїчастоти одного маятника, - це частота, на якій коливаються маятники. Роблять це в антифазі, що виражається математично тим, що одне коливання має синус, а інший - косинус (який, звичайно, просто синус зміщений\(\frac{\pi}{2}\)). Друга частота,\(\frac{1}{2}\left(\omega^{\prime}-\omega_{0}\right)\) набагато повільніше, і являє собою частоту, з якою два маятники передають енергію один одному, через пружину, яка їх з'єднує. На\(\PageIndex{1b}\) малюнку вона являє собою частоту огинаючої амплітуди коливання будь-якого з маятників. Всі ці явища повернуться в наступному розділі, при вивченні хвиль, які рухаються в середовищі, в якому багато осциляторів з'єднані один з одним (рис.\(\PageIndex{2}\)).

Малюнок\(\PageIndex{2}\): Дві пендули, що висять з рядка, є прикладом пари сполучених осциляторів. Зверніть увагу на зсув амплітуди від одного маятника до іншого за часом (суспільне надбання; Лукас проти Барбоза через Вікіпедію)

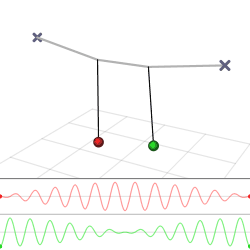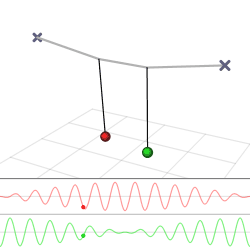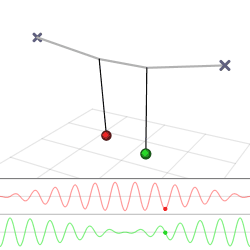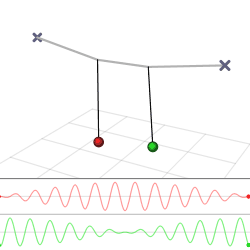
Звичайні режими

Для системи з лише двома осциляторами методика, яку ми використовували вище для розв'язання системи зв'язаних рівнянь\ ref {eqofmot1} та\ ref {eqofmot2}, є простою. Однак він не легко узагальнює системи з багатьма осциляторами. Натомість ми можемо використовувати той факт, що рівняння є лінійними і використовувати методи з лінійної алгебри (як ви, можливо, здогадалися з терміна власна частота). Ми можемо переписати рівняння\ ref {eqofmot1} і\ ref {eqofmot2} у вигляді матриці:

\[\frac{\mathrm{d}^{2}}{\mathrm{d} t^{2}}\left(\begin{array}{l}{\theta_{1}} \\ {\theta_{2}}\end{array}\right)=\left(\begin{array}{cc}{-\left(\omega_{0}^{2}+k\right)} & {k} \\ {k} & {-\left(\omega_{0}^{2}+k\right)}\end{array}\right)\left(\begin{array}{l}{\theta_{1}} \\ {\theta_{2}}\end{array}\right) \label{2oscmat}\]

Рівняння\ ref {2oscmat} - однорідне диференціальне рівняння другого порядку з постійними коефіцієнтами, сильно нагадує рівняння для простого, одновимірного гармонічного осцилятора. Отже, ми можемо очікувати, що рішення будуть виглядати схожими, тому ми намагаємося наш звичайний Ansatz:

\[\left(\begin{array}{l}{\theta_{1}} \\ {\theta_{2}}\end{array}\right)=\left(\begin{array}{l}{C_{1}} \\ {C_{2}}\end{array}\right) e^{i \omega t} \label{ansatz}\]

де\(C_1\) і\(C_2\) є константами. Заміна\ ref {ansatz} в\ ref {2oscmat} дає

\[\left(\begin{array}{cc}{\omega_{0}^{2}+k} & {-k} \\ {-k} & {\omega_{0}^{2}+k}\end{array}\right)\left(\begin{array}{c}{C_{1}} \\ {C_{2}}\end{array}\right)=\omega^{2}\left(\begin{array}{c}{C_{1}} \\ {C_{2}}\end{array}\right) \label{subrslt}\]

який ви, сподіваюся, визнають як проблему власного значення. Розв'язування для власних значень\(\omega ^2\) дає:

\[\left(-\omega^{2}+\omega_{0}^{2}+k\right)^{2}-k^{2}=0 \label{eigenval}\]

Розв'язки Equation\ ref {eigenval} не дивно відтворюють частоти незв'язаних рівнянь у розділі 8.4.1:

\[\omega_{+}^{2}=\omega_{0}^{2}, \quad \omega_{-}^{2}=\omega_{0}^{2}+2 k.\]

Власні вектори\ ref {subrslt} задаються

\[\boldsymbol{C}_{+}=\frac{1}{\sqrt{2}}\left(\begin{array}{l}{1} \\ {1}\end{array}\right) \quad \text { for } \quad \omega_{+} \quad \text { and } \quad \mathbf{C}_{-}=\frac{1}{\sqrt{2}}\left(\begin{array}{c}{1} \\ {-1}\end{array}\right) \quad \text { for } \quad \omega_{-}\]

Зверніть увагу, що власні вектори є ортогональними; це загальна властивість власних векторів симетричних матриць. Кожному власному вектору відповідає можливий сталий стан руху системи; ці стани відомі як нормальні режими («нормаль», що стосується ортогональності власних векторів). Тепер ми можемо відразу записати найзагальніше рішення Equation\ ref {2oscmat} як лінійну комбінацію власних режимів:

\[\left(\begin{array}{c}{\theta_{1}(t)} \\ {\theta_{2}(t)}\end{array}\right)=\frac{A_{+}}{2} e^{i\left(\omega_{+} t+\phi_{+}\right)}\left(\begin{array}{c}{1} \\ {1}\end{array}\right)+\frac{A_{-}}{2} e^{i\left(\omega_{-} t+\phi_{-}\right)}\left(\begin{array}{c}{1} \\ {-1}\end{array}\right)\]

де амплітуди\(A_{\pm}\) і фази\(\phi_{\pm}\) визначаються початковими умовами.

Написання нашої системи рівнянь у матричній формі дозволяє легко узагальнювати як до асиметричних конфігурацій (див. Задача 8.7), так і до систем з багатьма зв'язаними осциляторами. Важливим прикладом останнього випадку є дослідження коливань в твердих тілах. Атоми або іони в твердих тілах зазвичай утворюють кристалічну решітку, яку можна моделювати як велику кількість мас, з'єднаних пружинами. Такі кристали можуть мати складні коливальні властивості, які можна аналізувати за нормальними режимами. Зокрема, до режимів з низькою енергією зазвичай можна легко отримати доступ. Вони відомі як фонони і відповідають звуковим хвилям у твердому тілі.