5.2: Енергія і кількість частинок

Перш за все, зверніть увагу, що коливання макроскопічних змінних залежать від конкретних умов. ² Наприклад, в механічно- і теплоізольованої системі з фіксованим числом частинок, тобто членом мікроканонічного ансамблю, внутрішня енергія не коливається:\(\delta E = 0\). Однак якщо така система знаходиться в тепловому контакті з навколишнім середовищем, тобто є членом канонічного ансамблю (рис.\(2.4.1\)), то справа йде інакше. Дійсно, для такої системи ми можемо застосувати загальне рівняння (\(2.1.7\)), з\(W_m\) заданим розподілом Гіббса (\(2.4.7\)) - (\(2.4.8\)) не тільки до,\(E\) але й до\(E^2\). Як ми вже знаємо з п. 2.4, перший середній,

\[\langle E \rangle = \sum_m W_m E_m , \quad W_m = \frac{1}{Z} \exp \left\{ - \frac{E_m}{T}\right\}, \quad Z = \sum_m \exp \left\{- \frac{E_m}{T}\right\}, \label{15}\]

дає Equation (\(2.4.10\)), який може бути переписаний у вигляді

\[\langle E \rangle = \frac{1}{Z} \frac{\partial Z}{\partial (- \beta )}, \quad \text{ where } \beta \equiv \frac{1}{T}, \label{16}\]

зручніше для наших поточних цілей. Проведемо аналогічний розрахунок для\(E^2\):

\[\langle E^2 \rangle = \sum_m W_m E^2_m = \frac{1}{Z} \sum_m E^2_m \exp \{-\beta E_m \}. \label{17}\]

За допомогою подвійної диференціації можна перевірити, що останній вираз може бути переписано у формі, подібній до Equation (\ ref {16}):

\[\left\langle E^{2}\right\rangle=\frac{1}{Z} \frac{\partial^{2}}{\partial(-\beta)^{2}} \sum_{m} \exp \left\{-\beta E_{m}\right\} \equiv \frac{1}{Z} \frac{\partial^{2} Z}{\partial(-\beta)^{2}} . \label{18}\]

Тепер користуватися Eqs легко. (\(5.1.4-5.1.5\)) для обчислення дисперсії коливань енергії:

\[\left\langle\widetilde{E}^{2}\right\rangle=\left\langle E^{2}\right\rangle-\langle E\rangle^{2}=\frac{1}{Z} \frac{\partial^{2} Z}{\partial(-\beta)^{2}}-\left(\frac{1}{Z} \frac{\partial Z}{\partial(-\beta)}\right)^{2} \equiv \frac{\partial}{\partial(-\beta)}\left(\frac{1}{Z} \frac{\partial Z}{\partial(-\beta)}\right)=\frac{\partial\langle E\rangle}{\partial(-\beta)}. \label{19}\]

Починаючи з Eqs. (\ ref {15}) - (\ ref {19}) дійсні тільки в тому випадку, якщо обсяг системи\(V\) фіксований (оскільки його зміна може вплинути на енергетичний спектр\(E_m\)), цей важливий результат прийнято переписувати наступним чином:

Коливання\(E\):

\[\boxed{ \langle \tilde{E}^2 \rangle = \frac{\partial \langle E \rangle}{\partial (-1 / T) } = T^2 \left( \frac{\partial \langle E \rangle}{\partial T } \right)_V \equiv C_V T^2 . } \label{20}\]

Це надзвичайно простий, фундаментальний результат. Як перевірка осудності, для системи\(N\) аналогічних, незалежних частинок,\(\langle E \rangle\) а значить,\(C_V\) пропорційні\(N\), так що\(\delta E \propto N^{1/2}\) і\(\delta E/\langle E\rangle \propto N^{–1/2}\), відповідно до Equation (\(5.1.13\)). Дозвольте мені підкреслити, що класично виглядає рівняння (\ ref {20}) засноване на загальному розподілі Гіббса, і, отже, діє для будь-якої системи (класичної або квантової) в тепловій рівновазі.

Деякі наслідки цього результату будуть розглянуті в наступному розділі, а тепер давайте проведемо дуже схожий розрахунок для системи,\(N\) кількість частинок якої в системі не фіксована, тому що вони можуть йти і надходити з її середовища за бажанням. Якщо хімічний потенціал\(\mu\) навколишнього середовища і його температура\(T\) зафіксовані, тобто ми маємо справу з грандіозним канонічним ансамблем (рис.\(2.7.1\)), ми можемо використовувати грандіозний канонічний розподіл (\(2.7.5\)) - (\(2.7.6\)):

\[W_{m,N} = \frac{1}{Z_G} \exp \left\{\frac{\mu N - E_{m,N}}{T}\right\}, \quad Z_G = \sum_{N,m} \exp \left\{\frac{\mu N - E_{m,N}}{T}\right\}. \label{21}\]

Діючи точно так, як ми робили вище для внутрішньої енергії, отримуємо

\[\langle N \rangle = \frac{1}{Z_G} \sum_{m,N} N \exp \left\{\frac{\mu N - E_{m,N}}{T}\right\} = \frac{T}{Z_G} \frac{\partial Z_G}{\partial \mu }, \label{22}\]

\[\langle N^2 \rangle = \frac{1}{Z_G} \sum_{m,N} N^2 \exp \left\{\frac{\mu N - E_{m,N}}{T}\right\} = \frac{T^2}{Z_G} \frac{\partial^2 Z_G}{\partial \mu^2 }, \label{23}\]

так що дисперсія числа частинок

Коливання\(N\):

\[\boxed{ \left\langle\widetilde{N}^{2}\right\rangle=\left\langle N^{2}\right\rangle-\langle N\rangle^{2}=\frac{T^{2}}{Z_{G}} \frac{\partial Z_{G}}{\partial \mu}-\frac{T^{2}}{Z_{G}^{2}}\left(\frac{\partial Z_{G}}{\partial \mu}\right)^{2}=T \frac{\partial}{\partial \mu}\left(\frac{T}{Z_{G}} \frac{\partial Z_{G}}{\partial \mu}\right)=T \frac{\partial\langle N\rangle}{\partial \mu}, } \label{24}\]

в повній аналогії з рівнянням (\ ref {19}).

Зокрема, для ідеального класичного газу ми можемо об'єднати останній результат з Equation (\(3.2.2\)). (Як вже було підкреслено в п. 3.2, хоча цей результат був отриманий для канонічного ансамблю, в якому\(N\) зафіксовано кількість частинок, при\(N >> 1\) коливаннях\(N\) в грандіозному канонічному ансамблі повинні бути відносно невеликими, так що таке ж відношення має бути справедливим для середній\(\langle N\rangle\) в тому ансамблі.) Легко вирішуючи Equation (\(3.2.2\)) для\(\langle N\rangle \), отримуємо

\[\langle N \rangle = \text{const} \times \exp \left\{\frac{\mu}{T}\right\}, \label{25}\]

де «const» означає постійну множника при частинному диференціації\(\langle N \rangle\) над\(\mu \), що вимагається рівнянням (\ ref {24}). Виконуючи диференціювання, а потім знову використовуючи Equation (\ ref {25}),

\[\frac{\partial \langle N \rangle }{\partial \mu } = \text{const} \times \frac{1}{T} \exp \left\{\frac{\mu}{T}\right\} = \frac{\langle N \rangle }{T}, \label{26}\]

отримуємо з Equation (\ ref {24}) дуже простий результат:

Коливання\(N\): класичного газу

\[\boxed{ \langle \tilde{N}^2 \rangle = \langle N \rangle, \quad \text{ i.e. } \delta N = \langle N \rangle^{1/2} . } \label{27}\]

Це відношення настільки важливо, що я також покажу, як воно може бути виведено по-різному. Як побічний продукт цієї нової деривації доведемо, що цей результат справедливий для систем з довільним (скажімо, малим)\(N\), а також отримаємо більш детальну інформацію про статистику коливань цього числа. Розглянемо ідеальний класичний газ\(N_0\) частинок в об'ємі\(V_0\), і обчислимо ймовірність\(W_N\) мати саме\(N \leq N_0\) ці частинки в своїй частині об'єму\(V \leq V_0\) — див\(\PageIndex{1}\). Рис.

Рисунок\(\PageIndex{1}\): Виведення біноміальних і Пуассонових розподілів.

Для однієї частинки така ймовірність є\(W = V/V_0 = \langle N\rangle /N_0 \leq 1\), тоді як ймовірність мати цю частку в решті частини об'єму є\(W' = 1 – W = 1 – \langle N\rangle /N_0\). Якби всі частинки були помітні, ймовірність наявності\(N \leq N_0\) специфічних частинок в обсязі\(V\) і\((N – N_0)\) специфічних частинок в обсязі\((V – V_0)\), була б\(W^NW^{\prime (N_0-N)}\). Однак, якщо ми не хочемо розрізняти частинки, ми повинні помножити цю ймовірність на кількість можливих комбінацій частинок, зберігаючи числа\(N\) і\(N_0\) постійні, тобто на біноміальний коефіцієнт\(N_0!/N!(N_0 – N)!\). ³ В результаті необхідна ймовірність

Біноміальний розподіл:

\[\boxed{W_N = W^N W^{'(N_0-N)} \frac{N_0!}{N!(N_0 - N)!} = \left(\frac{\langle N \rangle }{N_0} \right)^N \left(1-\frac{\langle N\rangle}{N_0}\right)^{N_0-N} \frac{N_0!}{N!(N_0 - N)!}. } \label{28}\]

Це так званий біноміальний розподіл ймовірностей, дійсний для будь-яких\(\langle N\rangle\) і\(N_0\). ⁴

Як і раніше зберігаючи\(\langle N\rangle\) довільний, ми можемо спростити біноміальний розподіл, припускаючи\(V_0\), що весь обсяг\(N_0\), а значить, дуже великий:

\[ N_0 >> N , \label{29}\]

де\(N\) означає всі цінності, що цікавлять, в тому числі\(\langle N\rangle \). Дійсно, в цій межі ми можемо знехтувати\(N\)\(N_0\) в порівнянні з другим показником Рівняння (\ ref {28}), а також наблизити дріб\(N_0!/(N_0 – N)!\), тобто добуток\(N\) термінів\((N_0 – N + 1) (N_0 – N + 2)...(N_0 – 1)N_0\), на справедливість\(N_0^N\). В результаті отримуємо

\[W_N \approx \left( \frac{\langle N \rangle}{N_0 } \right)^N \left( 1 - \frac{\langle N \rangle}{N_0 } \right)^{N_0} \frac{N_0^N}{N!} \equiv \frac{\langle N \rangle^N}{N! } \left(1 - \frac{\langle N \rangle}{N_0 } \right)^{N_0} = \frac{\langle N \rangle^N}{N! } \left[ (1-W)^{\frac{1}{W}} \right]^{\langle N \rangle } , \label{30}\]

де, як і раніше,\(W = \langle N\rangle /N_0\). У межі (\ ref {29})\(W \rightarrow 0\), так що множник всередині квадратних дужок прагне до\(1/e\), зворотний натуральному логарифму основи. ⁵ Таким чином, ми отримуємо вираз, незалежний від\(N_0\):

Розподіл Пуассона:

\[\boxed{ W_N = \frac{\langle N \rangle^N}{N!} e^{-\langle N \rangle }. } \label{31}\]

Це дуже знаменитий розподіл Пуассона ⁶, який описує дуже широке сімейство випадкових явищ. \(\PageIndex{2}\)На малюнку показано цей розподіл для декількох значень\(\langle N\rangle\) — які, на відміну від\(N\), не обов'язково є цілими.

Малюнок\(\PageIndex{2}\): Розподіл Пуассона для декількох значень\(\langle N\rangle \). На відміну від цього середнього, аргумент\(N\) може приймати лише цілі значення, так що рядки на цих графіках є лише напрямними для циклу.

Гаусове розподіл:

\[\boxed{W_N = \frac{1}{(2\pi )^{1/2} \delta N} \exp \left\{ - \frac{(N - \langle N \rangle )^2}{2(\delta N )^2 } \right\} . } \label{32}\]

(Зауважте, що розподіл по Гаусу також дійсний, якщо\(N_0\) обидва\(N\) і великі, незалежно від співвідношення між ними — див\(\PageIndex{3}\). Рис.)

Малюнок\(\PageIndex{3}\): Ієрархія трьох основних розподілів ймовірностей.

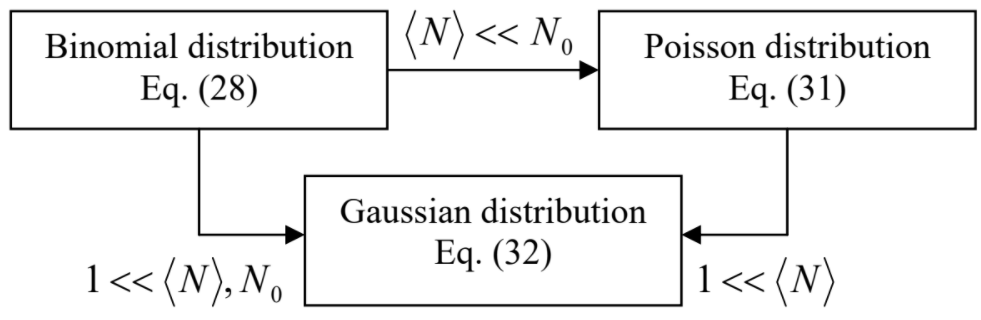
Основна властивість розподілу Пуассона (а отже, і Гауссона) полягає в тому, що він має ту саму дисперсію, що і рівняння (\ ref {27}):

\[\langle \tilde{N}^2 \rangle \equiv \left\langle ( N - \langle N \rangle )^2 \right\rangle = \langle N \rangle . \label{33}\]

(Це не вірно для загального біноміального розподілу.) Для наших сучасних цілей це означає, що для ідеального класичного газу Equation (\ ref {27}) діє для будь-якої кількості частинок.