6.3: Ван дер Ваальс та інші гази

Ми бачили, що справжні гази нагадують ідеальний газ тільки при низьких тисках і високих температурах. Були зроблені різні спроби знайти рівняння, яке адекватно представляє співвідношення між P, V і T для реального газу - тобто знайти рівняння стану для реального газу. Деякі з цих спроб були чисто емпіричними спробами пристосувати математичну формулу до реальних даних. Інші є результатом принаймні спроби описати якусь фізичну модель, яка б пояснила поведінку реальних газів. Зразок деяких більш простих рівнянь, які були запропоновані наступним чином:

Рівняння ван дер Ваальса:

\[ \left( P + \frac{a}{V^2} \right) (V - b) = RT.\]

Рівняння Бертело:

\[ \left( R + \frac{a}{ \left( TV^2 \right)} \right) (V - b) = RT.\]

Рівняння Клаузіуса*:

\[ \left( P + \frac{a}{T(V+c)^2} \right) (V-b) = RT.\]

Рівняння Дітерічі:

\[ P (V-b)e^{ \frac{a}{(RTV)}} = RT.\]

Редліх-Квонг:

\[ P = \frac{RT}{V-b} - \frac{a}{bT^{ \frac{1}{2}}} \left( \frac{1}{V} - \frac{1}{V + b} \right).\]

Віріальне рівняння:

\[ PV = A +BP + CP^2 + DP^3 + ...\]

*У рівнянні Клаузіуса, якщо ми виберемо c = 3b, ми отримаємо досить хорошу згоду між критичним коефіцієнтом стиснення газу Клаузіуса та багатьма реальними газами. Значення «критичного коефіцієнта стиснення» та розрахунок його значення для газу Клаузіуса описано трохи пізніше в цьому розділі.

Є багато інших, але на сьогоднішній день найвідомішим з них є рівняння ван дер Ваальса, яке я опишу в деякій довжині.

Голосова скринька англійського мовця не може правильно вимовити ім'я ван дер Ваальс, хоча W вимовляється більше як V, ніж W, і, на моє вухо, v є дещо проміжним між a v і f Щоб почути його правильно вимовлений - особливо голосні - ви повинні запитати a носій голландської мови. Часте написання «рівняння ван дер Ваала» є лише ще одним симптомом сучасного плачевного незнання використання апострофа, про який так сильно шкодувала Лінн Трасс.

Одиниці, в яких повинні виражатися константи a і b, іноді викликають труднощі, і вони залежать від того, чи призначений символ V в рівнянні для означати питомий або молярний об'єм. Наступне може бути корисним.

Якщо V призначений для означення питомого об'єму, слід записати рівняння ван дер Ваальса\( \left( P + a/V^2 \right) (V-b) = RT/ \mu\), де μ - молярна маса («молекулярна маса»). У цьому випадку розміри та одиниці СІ a становлять M ⁻¹ L ⁵ T ⁻² та Pa m ⁶ кг ⁻², а розміри та одиниці SI b складають M ⁻¹ L ³ та m ³, кг ⁻¹

Якщо V призначений для означення молярного об'єму, рівняння ван дер Ваальса слід записати в його звичній формі\( \left( P + a/V^2 \right) (V-b) = RT\). У цьому випадку розмірами та одиницями СІ a є ML ⁵ T ⁻² моль ⁻² та Pa m ⁶ кмоль ⁻², а розміри та одиниці SI b складають L ³ моль ⁻¹ та m ³ кмоль ⁻¹.

Константи ван дер Ваальса, що відносяться до молярного об'єму, H2O і CO2 приблизно:

Н ₂ О: а = 5,5 × 10 ⁵ Па м ⁶ кмоль ^−2. b = 3,1 × 10 ⁻² м ³ кмоль ⁻¹

СО ₂: а = 3,7 × 10 ⁵ Па м ⁶ кмоль ⁻² б = 4,3 × 10 ⁻² м ³ кмоль ⁻¹

Рівняння ван дер Ваальса має своє походження принаймні в деякій спробі описати фізичну модель реального газу. Властивості ідеального газу можна змоделювати, припускаючи, що газ складається з сукупності молекул нульового ефективного розміру і ніяких сил між ними, а тиск є результатом зіткнень зі стінками судини, що містить. У моделі ван дер Ваальса передбачається наявність привабливих сил між молекулами. Вони відомі як сили ван дер Ваальса і тепер розуміють, що виникають, тому що коли одна молекула наближається до іншої, кожна індукує дипольний момент в іншій, а два індукованих диполя потім приваблюють один одного. Ця сила привабливості зменшує тиск на стінках, зменшення пропорційно кількості молекул на стінках, які притягуються молекулами під ними, і кількості молекул під ними, які роблять притягання. Обидва обернено пропорційні V, тому тиск у рівнянні стану доводиться замінювати вимірюваним тиском P плюс членом, обернено пропорційним V ². Далі самі молекули займають кінцевий обсяг. Це рівносильно тому, що на дуже близькій відстані існують сили відштовхування (тепер розуміються як кулонівські сили), які більші за привабливі сили ван дер Ваальса. Таким чином, об'єм, в якому молекули вільно блукають, повинен бути зменшений у рівнянні ван дер Ваальса. Детальніше про сили між молекулами див. Розділ 6.8.

Якими б переконливими чи інакше ви не знайшли ці аргументи, вони є принаймні спробою описати деяку фізику, вони представляють поведінку реальних газів краще, ніж ідеальне рівняння газу, і, якщо нічого іншого, вони дають нам можливість трохи практикувати математику.

Коротко побачимо, як можна визначити константи a і b за вимірами критичних параметрів. Ці константи, в свою чергу, дають нам деяку вказівку на силу сил ван дер Ваальса та розміру молекул.

Рівняння Ван дер Ваальса, рівняння 6.3.1, можна записати

\[ P = \frac{RT}{V-b} - \frac{a}{V^2}.\]

Горизонтальна точка перегину виникає там, де\( \frac{\partial P}{\partial V}\) і\( \frac{\partial ^2 P}{\partial V^2}\) є нулем. Тобто

\[ - \frac{RT}{(V-b)^2} + \frac{2a}{V^3} = 0\]

і

\[ \frac{2TR}{(V-b)^3} - \frac{6a}{V^4} = 0.\]

Усуньте RT/a з них, щоб знайти критичний молярний об'єм газу ван дер Ваальса:

\[ V_c = 3b.\]

Підставте це рівняння 6.3.8 або 6.3.9 (або обидва, як перевірка вашої алгебри), щоб отримати критичну температуру:

\[ T_c = \frac{8a}{27Rb}.\]

Замініть рівняння 6.3.10 і 6.3.11 в рівняння 6.3.7 для отримання критичного тиску:

\[ P_c = \frac{a}{27b^2}.\]

З них ми з готовністю отримуємо

\[ \frac{P_c V_c}{RT_c} = \frac{3}{8} = 0.375.\]

Цю величину часто називають критичним коефіцієнтом стиснення або критичним коефіцієнтом стисливості, і позначимо її символом Z _c. Для багатьох реальних газів Z _c становить близько 0,28; таким чином рівняння ван дер Ваальса, хоча і корисне при якісному обговоренні властивостей газів, не відтворює спостережуваний критичний коефіцієнт стиснення особливо добре.

Підставимо тепер\( p = P/P_c,~ v = V/V_c,~ t = T/T_c,\) і рівняння ван дер Ваальса, в якому тиск, обсяг і температура виражаються через їх критичні значення, стає

\[ (p + 3/v^2)(v - \frac{1}{3} ) = \frac{8}{3} t.\]

Це також може бути написано

\[ 3pv^3 -(p+8t)v^2+9v-3 =0.\]

Для обсягів менше третини критичного об'єму це рівняння взагалі не описує поведінку реального газу. Дійсно, ви можете бачити, що p = ∞ коли v = 1/3, а це означає, що вам доведеться чинити нескінченний тиск, щоб стиснути газ ван дер Ваальса до третини його критичного об'єму. Можливо, ви захочете дослідити для себе поведінку рівнянь 6.3.14 та 15 для обсягів, менших за цей. Ви побачите, що він переходить до нескінченності при v = 0 і 1/3, і він має максимум між цими двома томами. Але рівняння представляє фізичний інтерес лише для v > 1/3, де зміна тиску, об'єму та температури має хоча б деяку схожість з поведінкою реальних газів, якщо ні в якому разі не точним. На малюнку VI.2 я показую поведінку газу ван дер Ваальса для п'яти температур - одна вище критичної температури, одна при критичній температурі і три нижче критичної температури. Локус максимумів і мінімумів знайдено шляхом усунення t між рівнянням 6.3.14 і p /v = 0. Ви повинні спробувати це, і показати, що локус максимумів і мінімумів (які я показав синьою лінією на малюнку VI.2) задається

\[ p = \frac{3}{v^2} - \frac{2}{v^3}\]

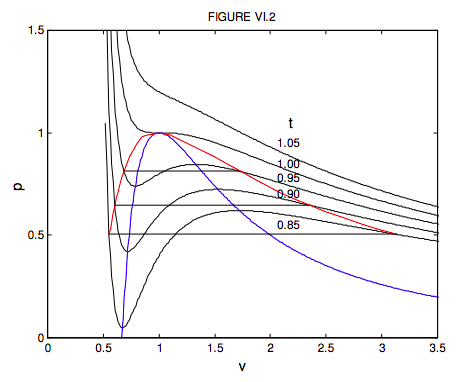
Не плутайте синю криву на цьому малюнку (вона показує локус максимумів і мінімумів) з пунктирною кривою на малюнку VI.1 (вона показує межу між фазами.). Для температур 0,85, 0,90 і 0,95 я намалював лінії постійного тиску, де рідина і пара знаходяться в рівновазі в реальній рідині. Вони намальовані так, що вони ділять криву ван вера Ваальса на дві рівні області, зверху і знизу. Це означає, що робота, виконана реальною рідиною, коли вона змінюється від рідини до пари при постійному тиску, дорівнює роботі, яка буде виконана її гіпотетичним еквівалентом ван дер Ваальса вздовж його хиткого шляху. Пізніше ми побачимо, що розміщення горизонтальної лінії є наслідком того, що функція Гіббса (яку ми ще не зустрічали) постійна, поки рідина і пар знаходяться в рівновазі. Пунктирна лінія малюнка VI.1 відповідала б на малюнку VI.2 локусу кінців горизонтальних ліній. Я намалював цей локус, який окреслює область, де рідина і пара знаходяться в рівновазі, червоним кольором на малюнку VI.2. Хоча рівняння ван дер Ваальса є лише грубим наближенням до поведінки реальних газів, проте вірно, що якщо тиск, температури та молярні обсяги виражаються через критичні тиску, температури та молярні обсяги, фактичні рівняння стану реальних газів дуже схожі. Кажуть, що два гази з однаковими значеннями p, v і t знаходяться у відповідних станах, а спостереження, що відношення p: v: t приблизно однакове для всіх газів, називається Законом відповідних держав. Ми можемо думати, що гази складаються з частинок (молекул), і єдина різниця між різними газами полягає в розмірах їх молекул (тобто їх різних констант ван дер Ваальса b) та їх дипольних моментах або їх електричних поляризаціях (тобто їх різних ван дер Ваальса) а константи). У безрозмірних формах рівняння стану ці константи ван дер Ваальса видаляються з рівнянь, і не дивно, що всі гази потім відповідають одному рівнянню стану.

Я залишаю читачеві показати, що для газу Бертело критичний молярний об'єм, температура і тиск і критичний коефіцієнт стиснення, відповідно, 3 b\( \sqrt{\frac{8 a}{27 b R}}\),\( \frac{1}{b} \sqrt{\frac{a R}{216 b}}\) і 0.375, що рівняння стану з точки зору безрозмірних змінних є

\[ p=\frac{8 t}{3 v-1}-\frac{3}{t v^{2}} ,\]

і що локус максимумів і мінімумів

\[ p=\frac{1}{v^{1 / 2}}\left(\frac{4}{v}-\frac{6}{3 v-1}\right) .\]

Вони показані на малюнку VI.2a. Буде відзначено, що критичний коефіцієнт стиснення такий же, як (а значить, і не краще) для газу ван дер Ваальса.

Для газу Клаузіуса критичний молярний об'єм, температура і тиск і критичний коефіцієнт стиснення складають відповідно 3 b + 2 c,\( \sqrt{\frac{8 a}{27(b+c) R}}, \frac{1}{(b+c)} \sqrt{\frac{a R}{216(b+c)}}\) і\( \frac{3 b+2 c}{8(b+c)}\).

Якщо c = 3 б., то вони стають 3 c,\( \sqrt{\frac{2 a}{9 c R}}, \frac{1}{c} \sqrt{\frac{a R}{512 c}}\) і\( \frac{9}{32}=0.28125\). Я вибираю c = 3 b, оскільки це дає хорошу згоду з критичним коефіцієнтом стиснення для багатьох реальних газів. У безрозмірних одиницях рівняння Клаузіуса стає

\[ p=\frac{32 t}{9 v-1}-\frac{48}{t(3 v+1)^{2}}\]

Локус максимумів і мінімумів дорівнює

\[ p=\frac{1}{\sqrt{1+3 v}}\left(\frac{80-144 v}{1-6 v-27 v^{2}}\right)=\frac{16(5-9 v)}{(1-9 v)(1+3 v)^{3 / 2}}\]

Вони показані на малюнку VI.2b

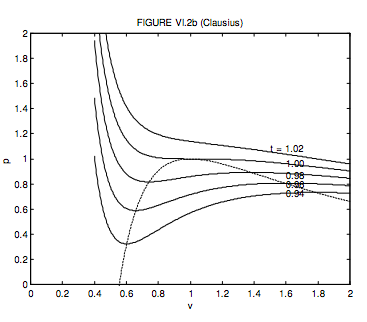
Рівняння Клаузіуса було важкою працею. Діетериці трохи простіше. Критичний молярний обсяг, температура і тиск і критичний коефіцієнт стиснення складають відповідно 2 b,\( \frac{a}{4 R b}, \frac{a}{4 e^{2} b^{2}}\) а 2/ e ² = 0,271. Відзначимо, що критичний коефіцієнт стиснення набагато ближче до коефіцієнта багатьох реальних газів. Безрозмірна форма рівняння Дітерічі

\[ p=\frac{t}{2 v-1} \exp \left(2-\frac{2}{t v}\right) .\]

Локус максимумів і мінімумів дорівнює

\[ p=\frac{1}{v^{2}} \exp \left(\frac{2(v-1)}{2 v-1}\right) .\]

Вони показані на малюнку VI.2c.

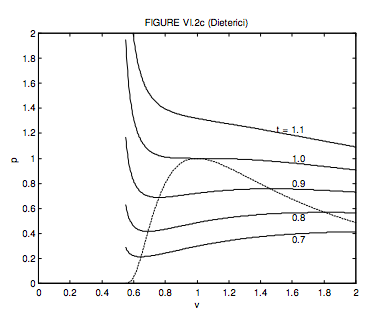
Рівняння Редлиха-Квонга, як і у ван дер Ваальса, Бетелота та Дітерічі, має лише два параметри (a та b). Всі вони не дуже погані при температурах, помітно вище критичної температури, але, близьке до критичної температури, емпіричне рівняння Редліха-Квонга узгоджується трохи краще, ніж рівняння ван дер Ваальса робить з тим, що спостерігається для реальних газів. Отримання критичних констант за параметрами здійснюється точно таким же методом, що і для ван дер Ваальса та інших рівнянь, але вимагає, мабуть, трохи більше праці і терпіння. Читач може захотіти (або не сподобатися) спробувати його. За критичні константи я отримую

\[ V_{\mathrm{c}}=x b,\]

\[ T_{\mathrm{c}}=y\left(\frac{a}{b R}\right)^{2 / 3} \]

і

\[ P_{c}=z\left(\frac{a^{2} R}{b^{5}}\right)^{1 / 3} ,\]

де

\[ x=3.847322100\]

\[ y=0.345039996\]

і

\[ z=0.029894386.\]

Критичний коефіцієнт стиснення - xz/y, який дорівнює рівно 1/3. Це не так близько до коефіцієнта стиснення багатьох реальних газів, як критичний коефіцієнт стиснення Dieterici.

Ми можемо інвертувати ці рівняння, щоб отримати вирази для a та b з точки зору критичної температури та тиску (або температури та обсягу, або тиску та обсягу). Таким чином

\[ a=u\left(\frac{R^{2} T_{c}^{5 / 2}}{P_{\mathrm{c}}}\right) \]

і

\[ b=w \frac{R T_{\mathrm{c}}}{P_{\mathrm{c}}} ,\]

де

\[ u=0.427480233\]

і

\[ w=0.086640350. \]

(Ви також можете зробити це для інших рівнянь стану, звичайно.)

Для того, щоб відтворити ці результати, вам доведеться трохи попрацювати, щоб побачити, звідки беруться всі константи. Виходить, що значення константи х - це позитивний дійсний корінь рівняння

\[ x^{3}-3 x^{2}-3 x-1=0. \]

У наведеному вище аналізі я отримав всі константи з числового рішення рівняння 6.3.33, але рішення цього рівняння (і всіх наступних констант) можна записати і в сурдах. Таким чином, з\( f=\sqrt[3]{2}-1, \quad g=\sqrt[3]{4}-1, \quad h=\sqrt[3]{16}-1 \), константи можна обчислити з

\[ x=\frac{1}{f}, \quad y=g^{2}, \quad z=\frac{3-5 g}{g+h}, \quad u=\frac{1}{9 f} \text { and } w=\frac{1}{3} f. \]

Якщо тепер ввести безрозмірні змінні\( p=P / P_{\mathrm{c}}, v=V N_{\mathrm{c}}, t=T / T_{\mathrm{c}}\), і підставити ці та рівняння 6.3.23-25 в рівняння 6.3.6, то отримаємо безрозмірне рівняння Редліха-Квонга

\[ p=\frac{l t}{x v-1}-\frac{1}{m t^{1 / 2}}\left(\frac{1}{x v}-\frac{1}{x v+1}\right) ,\]

де

\[ l=y / z=11.54196631 \quad \text { and } \quad m=g z=0.017559994.\]

Безрозмірне рівняння Редліха-Квонга проілюстровано на малюнку VI.2D. Я не намагався знайти явне рівняння для локусу максимумів, але замість цього я обчислював його чисельно, проілюстровано пунктирною лінією на малюнку VI.2D.

Ось короткий виклад результатів для двопараметричних рівнянь стану:

\[ \begin{matrix} ~ & P_c & V_c & T_c & Z_c & a & b \\ \text{Van der Waals} & \frac{a}{27 b^{2}} & 3b & \frac{8 a}{27 R b} & \frac{3}{8} & \frac{27 R^{2} T_{\mathrm{c}}^{2}}{64 P_{\mathrm{c}}} & \frac{R T_{\mathrm{c}}}{8 P_{\mathrm{c}}} \\ \text{Berthelot} & \frac{1}{b} \sqrt{\frac{a R}{216 b}} & 3b & \sqrt{\frac{8 a}{27 b R}} & \frac{3}{8} & \frac{27 R^{2} T_{\mathrm{c}}^{3}}{64 P_{\mathrm{e}}} & \frac{R T_{\mathrm{c}}}{8 P_{\mathrm{c}}} \\ \text{Dieterici} & \frac{a}{4 e^{2} b^{2}} & 2b & \frac{a}{4 R b} & 2 e^{-2} & \frac{R T_{\mathrm{c}}}{e^{2} P_{\mathrm{c}}} & \frac{4 R^{2} T_{\mathrm{c}}^{2}}{e^{2} P_{\mathrm{c}}} \\ \text{Redlich-Kwong} & z\left(\frac{a^{2} R}{b^{5}}\right)^{1 / 3} & xb & y\left(\frac{a}{b R}\right)^{2 / 3} & \frac{1}{3} & u\left(\frac{R^{2} T_{c}^{5 / 2}}{P_{c}}\right) & w \frac{R T_{\mathrm{c}}}{P_{\mathrm{c}}} \\ ~ & z = 0.0299 & x = 3.85 & y = 0.345 & u = 0.427 & w = 0.0866 \end{matrix}\]

Читач може спробувати відтворити їх (дайте мені знати ([e-mail]), якщо ви знайдете будь-які помилки!) або хоча б (корисна вправа) перевірити свої розміри. У розділі 6.2 ми згадували, що корисним способом вказати, як поведінка реального газу відрізняється від поведінки ідеального газу, є побудова коефіцієнта стиснення\( Z=\frac{P V}{R T}\) проти тиску. У міру наближення тиску до нуля коефіцієнт стиснення наближається до 1. Це відбувається тому, що молекули тоді настільки далеко один від одного, що між ними немає помітних сил (привабливих або відразливих). Оскільки тиск збільшується з нуля, коефіцієнт стиснення, як правило, спочатку падає трохи нижче 1, а потім піднімається вище 1 в міру збільшення тиску. Буде цікаво подивитися, як очікується, коефіцієнт стиснення буде змінюватися в залежності від тиску для різних «теоретичних» газів, про які ми обговорювали. Я зроблю це лише для газу ван дер Ваальса, і я використовую безрозмірну форму рівняння ван дер Ваальса, яке було вперше дано як рівняння 6.3.14:

\[ \left(p+3 / v^{2}\right)\left(v-\frac{1}{3}\right)=\frac{8}{3} t.\]

Коефіцієнт стиснення є\( Z=\frac{P V}{R T}\) і критичний коефіцієнт стиснення є\( Z_{c}=\frac{P_{c} V_{c}}{R T_{c}}\). З цього ми бачимо, що\( Z=\frac{p v}{t} Z_{c}\). Для ван дер Ваальса газу\( Z_{c}=\frac{3}{8}\), так що\( Z=\frac{3 p v}{8 t}\). На жаль, для того, щоб побудувати Z проти p для заданого t, ми повинні бути в змозі висловити v через p, що означає рішення рівняння 6.3.37, яке є кубічним рівнянням в\( v\left[3 p v^{3}-(p+8 t) v^{2}+9 v-3=0\right]\). Я зробив це чисельно, і я показую отримані графіки Z проти p для декількох температур, на малюнку VI.2e. Зверніть увагу, що при p = 1 і t = 1, (тобто в критичній точці) коефіцієнт стиснення дорівнює 0,375. Криві Z проти p для реальних газів мають однакову загальну форму, але точне узгодження числових деталей не зовсім добре. Де Z > 1, тиск більше, ніж у ідеального газу, b (відштовхуюча) частина рівняння ван дер Ваальса є більш важливою, ніж a (приваблива) частина. Де Z < 1, тиск менше, ніж у ідеального газу, а (приваблива) частина рівняння ван дер Ваальса є більш важливою, ніж b (відштовхуюча) частина. Я не досліджував, чи інші «теоретичні» рівняння держави роблять помітно краще. Чому б не піти собі?!

Малюнок VI.2e. Коефіцієнт стиснення Z = PV/ RT проти p (тиск в одиницях критичного тиску для газу ван дер Ваальса, для декількох значень t (температура в одиницях критичної температури.) Для газу ван дер Ваальса коефіцієнт стиснення більше 1 для всіх температур більше t = 27/8 = 3,375. При цій температурі коефіцієнт стиснення близький до 1 до р дорівнює приблизно 2, і ця температура відома як температура Бойла. При температурі Бойла крива Z: p плоска і близька до 1 для досить великого діапазону тисків. Таким чином, при температурі Бойла навіть неідеальний газ досить близько підпорядковується закону Бойла. Для газу ван дер Ваальса критична температура становить 8a/ (27Rb), тому температура Бойла для ван дер Ваальса становить a/ (Rb). Читач повинен обчислити це для H ₂ O та CO ₂, використовуючи значення констант ван дер Ваальса, наведених у цій главі. Крапка на t = 1,00 ізотерми при p = 1 і Z = 0,375 відповідає критичній точці. Кожен, хто відчуває потребу в більш розумових вправах, може захотіти запитати: Для якого значення p (крім нуля) є Z = 1. Наприклад, чи можете ви показати, що для t = 1, Z = 1 для p = 152/27 = 5.630?

Останнє запропоноване емпіричне рівняння стану, яке ми згадували, - це віріальне рівняння, рівняння 6.3.6:\( P V=A+B P+C P^{2}+D P^{3}+\ldots \) Це іноді записується у формі\(P V=A+\frac{B}{V}+\frac{C}{V^{2}}+\frac{D}{V^{3}} \ldots \), але в цих примітках ми будемо використовувати форму рівняння 6.3.6. Коефіцієнти A, B і т.д. називаються віріальними коефіцієнтами і є функціями температури. Перший коефіцієнт, А, якраз і є RT. Ми також можемо записати віріальне рівняння як

\[ Z=1+B^{\prime} P+C^{\prime} P^{2}+D^{\prime} P^{3}+\ldots \]

Ми могли б виміряти коефіцієнт B 'для реального газу шляхом побудови Z як функції тиску аналогічно малюнку VI.2e. \( \left(\frac{\partial Z}{\partial P}\right)_{T} \)Початковий нахил, екстрапольований на нульовий тиск, дає значення B '. При низьких температурах B 'негативний; при високих температурах B' позитивний. При температурі Бойла B 'дорівнює нулю, і при цій температурі коефіцієнт стиснення є одиницею для великого діапазону тисків, і газ відповідно тісно відповідає закону Бойла. Коефіцієнт C 'невеликий, тому термін C' P ² вступає в гру тільки при більш високих тисках. При більш високих тисках Z збільшується, показуючи, що C 'є позитивним коефіцієнтом. Коефіцієнт D 'менше, ніж C'

Всі математично «добре поводяться» рівняння стану нижче критичної температури мають максимум і мінімум — тобто крива показує «погойдування». Я ілюструю це на малюнку VI.2f. Це ізотерма ван дер Ваальса для t = 0,95 в безрозмірних змінних. Це те саме, що і одна з кривих, показаних на малюнку VI.2, намальована в іншому масштабі, щоб підкреслити «похитування».

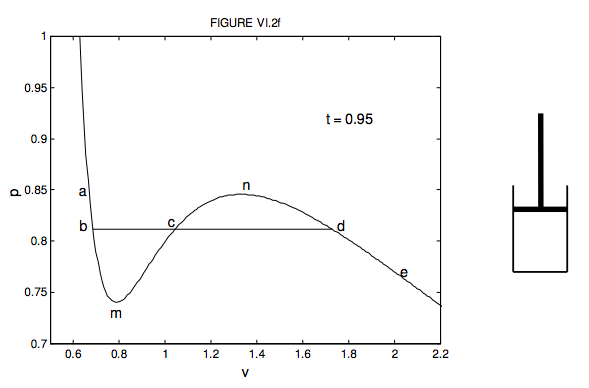
Використовуючи маленький циліндр і поршень праворуч від графіка, спробуйте уявити, що відбувається з закритою рідиною або парою, коли ви рухаєте поршень всередину і назовні при постійній температурі, рухаючись від a до e і назад на графіку. Почніть з е. Циліндр заповнений паром. Рухайте поршень всередину, йдучи від е до г; тиск збільшується, а обсяг зменшується. Тепер справжній газ не слідує за функцією ван дер Ваальса весь шлях. У d відбувається щось інше. Насправді можна взяти пари трохи повз d до (але не за межами) п. Це був би переохолоджений пар, наприклад, використовується в хмарній камері. Він відразу конденсується в лінію крапель рідини, як тільки заряджена частинка пролетить через пар. Однак зазвичай трапляється те, що частина пари починає конденсуватися як рідина, і ми рухаємося горизонтально від d до b. У міру того, як ми рухаємо поршень вниз при постійній температурі, обсяг звичайно зменшується, і все більше рідини конденсується таким чином, що тиск залишається постійним. У порції db у нас є рідина і пара, що існують разом в поршні, в термодинамічній рівновазі. Близько до кінця d є лише трохи рідини; близько до кінця b це майже вся рідина, залишилося лише трохи пари. Поза b, у напрямку a, простір повністю заповнюється рідиною. Ми можемо штовхати і штовхати, сильно підвищуючи тиск, але зміни обсягу дуже мало, тому що рідина майже (хоча і не зовсім) нестислива. Ізотерма там дуже крута. Насправді можна взяти рідину трохи від b до (але не за її межами) m без будь-якого його випаровування. Це була б перегріта рідина, наприклад, використовується в бульбашковій камері. Він негайно випаровується в лінію бульбашок, як тільки заряджена частинка пролетить через рідину.

Далі буде важливий матеріал щодо зміни стану в розділах 9 та 14. В даний час, однак, я хочу запитати: при якому тиску починається конденсація? Якщо говорити по-іншому, яка висота лінії bd на малюнку VI.2f? Я чув стверджував, що висота bd, (тиск, при якому відбувається конденсація) повинна бути такою, щоб площа bmc дорівнювала площі cnd. Я не впевнений, що повністю розумію аргументи, що призводять до цього висновку. Зрештою, реальний газ не відповідає рівнянню ван дер Ваальса або будь-якому з інших теоретичних/емпіричних рівнянь, які ми обговорювали. Але, можливо, не нерозумно намалювати бд таким, щоб області вище і під ним були рівні, і в будь-якому випадку це робить для цікавого (і складного) обчислювального вправи. Рівняння ван дер Ваальса в безрозмірних змінних дається як рівняння 6.3.14. Чи можете ви розрахувати тиск таким чином, щоб площа bmc нижче bd дорівнювала площі cnd над ним? Я роблю це p = 0,812, що є висотою, де я намалював його на малюнку. Я не робив обчислення для інших рівнянь. Я залишаю це тобі!