7.5: Проблеми з роботою лазера

Last updated
Save as PDF

Page ID: 78882

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

У цьому розділі ми розглянемо деякі проблеми, які виникають з лазерами, і обговоримо, що можна зробити для їх вирішення.

1. Множинні резонансні частоти

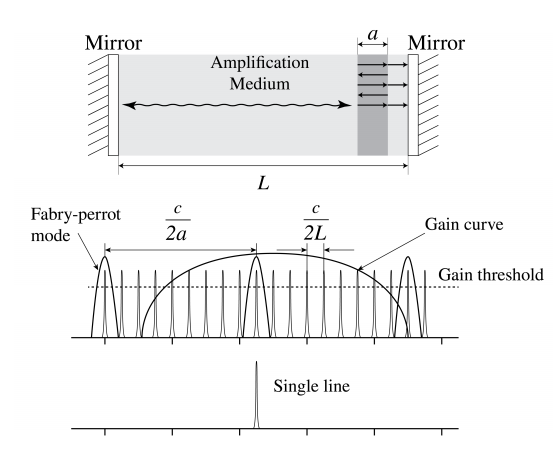
У багатьох додатках, таких як лазерний зв'язок та інтерферометрія, потрібна одна довжина хвилі. Розглянемо порожнину довжини,\(L\) як показано на малюнку,\(\PageIndex{1}\) і припустимо, що підсилювач має криву посилення, що охоплює багато резонансів резонатора. Один із способів досягнення одночастотного виходу - це подбати про те, щоб була лише одна частота, для якої коефіцієнт посилення більше, ніж втрати. Потім кажуть, що лазер вище порогу лише на одну частоту. Це можна зробити, вибравши\(L\) довжину порожнини настільки маленькою, що під кривою посилення є тільки один режим, для якого коефіцієнт посилення вище, ніж втрати. Однак невелика довжина підсилювача означає меншу вихідну потужність і менше колімований вихідний промінь. Іншим методом було б зменшити прокачування, щоб тільки за один режим посилення компенсував втрати. Але це знову ж таки означає, що вихідна потужність лазера відносно невелика. Кращим рішенням є додавання порожнини Фабри-Перо всередині лазерної порожнини, як показано на малюнку\(\PageIndex{2}\). Порожнина складається, наприклад, зі шматка скла певної товщини\(a\).

Вибравши\(a\) досить мале, відстань по частоті\(c /(2 a)\) між резонансами порожнини Фабри-Перо стає настільки великим, що під кривою посилення підсилювача залишається тільки один резонанс Фабрі-Перо. Крім того, вибравши правильний кут для порожнини Фабри-Перо по відношенню до осі порожнини лазера, резонанс Фабри-Перо можна поєднати з потрібною резонансною частотою. Ця частота тоді частота виходу лазера. Всі інші резонансні частоти резонатора під кривою посилення затухають, тому що вони не є резонансом порожнини Фабри-Перо.

7.5.1.jpg — Малюнок\(\PageIndex{1}\): Лазер з порожниною довжини\(L\) та широкою кривою посилення підсилювача. Багато резонансних частот резонансів вище порогових для компенсації втрат.

7.5.2.jpg — Малюнок\(\PageIndex{2}\): Лазер з порожниною довжини\(L\), широкою кривою посилення підсилювача та доданою порожниною Фабри-Перо. Резонанси FB діють як додатковий фільтр для вибору тільки одного режиму лазера.

2. Кілька поперечних режимів

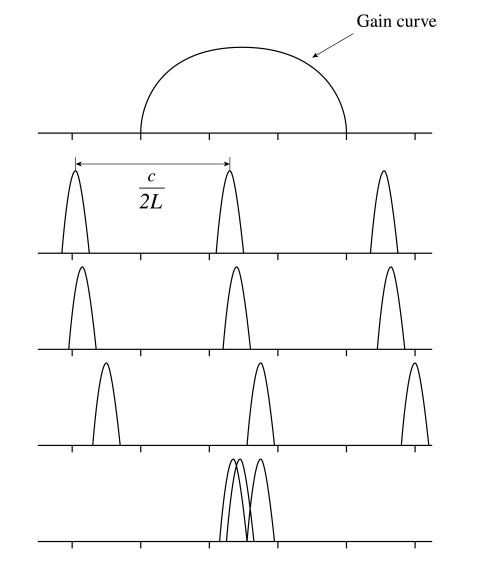
Найвідоміший лазерний режим має поперечний розподіл інтенсивності, який є гаусовою функцією поперечної відстані до оптичної осі. Моду з гауссовой поперечною формою ми називаємо поздовжньою, а коли її частота задовольняє\(\nu=m c /(2 L)\), її називають поздовжньою.\(m\) Однак всередині лазерної порожнини можуть резонувати і інші режими з різними поперечними малюнками. Приклад показаний на малюнку\(\PageIndex{3}\), де режим\((1,0)\) складається з двох максимумів. Існує ще багато поперечних режимів, як показано на малюнку\(\PageIndex{4}\).

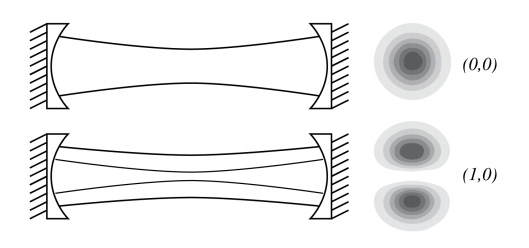
7.5.3.jpg — Малюнок\(\PageIndex{3}\): Лазерна порожнина з\((0,0)\) і\((1,0)\) режимами.

Поперечні режими всі мають трохи різні частоти. Так що навіть при наявності тільки одного гаусового режиму вище порогового (тобто режими відбуваються тільки для одного значення\(m\)), може бути багато поперечних режимів з частотами, дуже близькими до частоти гауссового режиму, які також вище порогових. Це проілюстровано на малюнку,\(\PageIndex{5}\) де\((0,0),(1,0)\) частоти режимів і\((1,1)\) все вище порогових. Зазвичай віддає перевагу режиму Гаусса, а поперечні режими небажані. Як від них позбутися? Оскільки режим Гаусса має найменшу поперечну ширину, поперечні режими можна усунути, вставивши діафрагму в порожнину лазера. Ця діафрагма настільки мала, що поперечні режими зазнають високих втрат на розсіювання, але досить велика, що режим Гаусса не впливає.

7.5.4.jpg — Малюнок\(\PageIndex{4}\): Інтенсивність малюнка декількох поперечних режимів.

7.5.5.png — Малюнок\(\PageIndex{5}\): Резонансні частоти поперечних режимів, які мають достатній коефіцієнт посилення для компенсації втрат.