7.3: Посилення
- Page ID
- 78857
Посилення може бути досягнуто середовищем з атомними резонансами, які знаходяться на або близькі до одного з резонансів резонатора. Вперше згадаємо просту теорію, розроблену Ейнштейном в 1916 році про динамічну рівновагу матеріалу при наявності електромагнітного випромінювання.
7.3.1 Коефіцієнти Ейнштейна
Розглянуто два рівня атомної енергії\(E_{2}>E_{1}\). Поглинаючи фотон енергії\[\hbar \omega=E_{2}-E_{1}, \nonumber \], атом, який спочатку знаходиться в нижчому енергетичному стані 1, може збуджуватися до стану 2. \(\hbar\)Ось константа Планка:\[\hbar=\frac{6.626070040}{2 \pi} \times 10^{-34} \quad \text { Js } . \nonumber \]
Припустимо\(W(\omega)\), усереднена за часом щільність електромагнітної енергії на одиницю частотного інтервалу навколо частоти\(\omega\). Звідси\(W\) має вимір Jsm\(^{3}\). \(N_{1}\)\(N_{2}\)Дозволяти і бути число атомів в стані 1 і 2, відповідно, де\[N_{1}+N_{2}=N, \nonumber \] загальна кількість атомів (яке є постійним). Швидкість поглинання - це швидкість зменшення\(N_{1}\) і пропорційна щільності енергії і кількості атомів в стані 1:\[\frac{d N_{1}}{d t}=-B_{12} N_{1} W(\omega), \quad \text { absorption, } \nonumber \] де константа\(B_{12}>0\) має розмірність\(\mathrm{m}^{3} \mathrm{~J}^{-1} \mathrm{~s}^{-2}\). Без будь-якого зовнішнього впливу атом, який знаходиться в збудженому стані, зазвичай переходить в стан 1 всередині\(1 \mathrm{~ns}\) або близько того, випромінюючи фотон енергії (7.10). Цей процес називається спонтанним випромінюванням, так як він відбувається і без присутнього електромагнітного поля. Швидкість спонтанного випромінювання задається:\[\frac{d N_{2}}{d t}=-A_{21} N_{2}, \quad \text { spontaneous emission, } \nonumber \] де\(A_{21}\) має розмірність\(\mathrm{s}^{-1}\). Термін служби мимовільної передачі становить\(\tau_{s p}=1 / A_{21}\). Важливо відзначити, що мимовільно випромінюється фотон випромінюється в випадковому напрямку. Крім того, оскільки випромінювання відбувається у випадковий час, між спонтанно випромінюваним полем і полем, яке збуджує атом, немає фазового зв'язку.
Менш очевидно, що при наявності електромагнітного поля частоти, близького до атомного резонансу, атом в збудженому стані також може стимулюватися цим полем для випромінювання фотона і переходу в нижчий енергетичний стан. Швидкість стимульованого випромінювання пропорційна кількості збуджених атомів і енергетичної щільності поля:\[\frac{d N_{2}}{d t}=-B_{21} N_{2} W(\omega), \quad \text { stimulated emission, } \nonumber \] де\(B_{21}\) має таку ж розмірність, що і\(B_{12}\). Дуже важливо зауважити, що стимульоване випромінювання відбувається в тому ж електромагнітному режимі (наприклад, плоска хвиля), що і режим поля, що збуджує передачу, і що фаза випромінюваного поля ідентична фазі збуджуючого поля. Це означає, що стимульоване випромінювання підсилює електромагнітне поле конструктивними перешкодами. Це властивість має вирішальне значення для роботи лазера.
7.3.2 Зв'язок між коефіцієнтами Ейнштейна
Відносини існують між коефіцієнтами Ейнштейна\(A_{21}, B_{12}\) і\(B_{21}\). Розглянемо чорне тіло, наприклад, закритий порожній ящик. Через певний час буде досягнуто теплова рівновага. Оскільки випромінювання не потрапляє в коробку ззовні і не залишає коробку назовні, щільність електромагнітної енергії - це теплова щільність\(W_{T}(\omega)\), яка, згідно із Законом Планка, не залежить від матеріалу, з якого виготовлена коробка, і дається:\[W_{T}(\omega)=\frac{\hbar \omega^{3}}{\pi^{2} c^{3}} \frac{1}{\exp \left(\frac{\hbar \omega}{k_{B} T}\right)-1}, \nonumber \] де \(k_{B}\)це константа Больцмана:\[k_{B}=1.38064852 \times 10^{-23} \mathrm{~m}^{2} \mathrm{kgs}^{-2} \mathrm{~K}^{-1} . \nonumber \]

Швидкість переходу атомів вгору і вниз в стінці коробки повинна бути однаковою:\[B_{12} N_{1} W_{T}(\omega)=A_{21} N_{2}+B_{21} N_{2} W_{T}(\omega) . \nonumber \]
Отже,\[W_{T}(\omega)=\frac{A_{21}}{B_{12} N_{1} / N_{2}-B_{21}} . \nonumber \]
Але в тепловій рівновазі:\[\frac{N_{2}}{N_{1}}=\exp \left(-\frac{E_{2}-E_{1}}{k_{B} T}\right)=\exp \left(-\frac{\hbar \omega}{k_{B} T}\right) . \nonumber \]
Підставляючи (\(\PageIndex{11}\)) в (\(\PageIndex{10}\)) і порівнюючи результат з (\(\PageIndex{7}\)), випливає, що обидва вирази for\(W_{T}(\omega)\) ідентичні для всіх температур, тільки якщо\[B_{12}=B_{21}, \quad A_{21}=\frac{\hbar \omega^{3}}{\pi^{2} c^{3}} B_{21} . \nonumber \]
Приклад Для зеленого світла\(\lambda=550 \mathrm{~nm}\), ми маємо\(\omega / c=2 \pi / \lambda=2.8560 \times 10^{6} \mathrm{~m}^{-1}\) і таким чином\[\frac{A_{21}}{B_{21}}=1.5640 \times 10^{-15} \mathrm{~J} \mathrm{~s} \mathrm{~m}^{-3} . \nonumber \]
Отже, спонтанні та стимульовані норми викидів рівні, якщо\(W(\omega)=1.5640 \times 10^{-15} \mathrm{Js} \mathrm{m}^{-3}\)
Для (вузької) смуги частот\(\mathrm{d} \omega\) усереднена за часом щільність енергії дорівнює,\(W(\omega) \mathrm{d} \omega\) а для плоської хвилі щільність енергії пов'язана з інтенсивністю\(I\) (тобто довжиною усередненого за часом вектора Пойнтінга) як:\[W(\omega) \mathrm{d} \omega=I / c . \nonumber \]
| \(I\left(\mathrm{~W} \mathrm{~m}^{-2}\right)\) | |
|---|---|
| ртутна лампа | \(10^{4}\) |
| Безперервний лазер | \(10^{5}\) |
| Імпульсний лазер | \(10^{13}\) |
Типовим значенням ширини частоти вузької емісійної лінії звичайного джерела світла є:\(10^{10} \mathrm{~Hz}\), т\(\mathrm{d} \omega=2 \pi \times 10^{10} \mathrm{~Hz}\). Отже, спонтанні та стимульовані показники викидів ідентичні, якщо інтенсивність є\(I=2.95 \times 10^{4} \mathrm{~W} / \mathrm{m}^{2}\). Як видно з таблиці 7.1, тільки для лазерного світла стимульоване випромінювання більше, ніж спонтанне випромінювання. Для класичних джерел світла швидкість спонтанного випромінювання набагато більше, ніж стимульована швидкість випромінювання. Якщо промінь з шириною\(\mathrm{d} \omega\) частоти і щільністю енергії\(W(\omega)\) d\(\omega\) поширюється через матеріал, швидкість втрати енергії пропорційна:\[\left(N_{1}-N_{2}\right) B_{12} W(\omega) . \nonumber \]
За даними (\(\PageIndex{9}\)) це дорівнює швидкості спонтанного викиду. Дійсно, мимовільно випромінюється світло відповідає втраті інтенсивності променя, тому що він випромінюється у випадкових напрямках і з випадковою фазою.
Коли\(N_{2}>N_{1}\), світло посилюється. Цей стан називається інверсією населення і воно має важливе значення для роботи лазера. Відзначимо, що співвідношення спонтанних і стимульованих скорочень викидів, відповідно до (\(\PageIndex{12}\)), пропорційно\(\omega^{3}\). Отже, для коротших довжин хвиль, таких як\(\mathrm{x}\) -промені, набагато складніше зробити лазери, ніж для видимого світла.
7.3.3 Інверсія населення
Для щільності електромагнітної енергії\(W(\omega)\) на одиницю частотного інтервалу рівняння швидкості є\[\begin{aligned} \frac{d N_{2}}{d t} &=-A_{21} N_{2}+\left(N_{1}-N_{2}\right) B_{12} W(\omega) \\ \frac{d N_{1}}{d t} &=A_{21} N_{2}-\left(N_{1}-N_{2}\right) B_{12} W(\omega) \end{aligned} \nonumber \]
Звідси, для\(\Delta N=N_{2}-N_{1}\):\[\frac{d \Delta N}{d t}=-A_{21} \Delta N-2 \Delta N B_{12} W(\omega)-A_{21} N \nonumber \] де, як раніше:\(N=N_{1}+N_{2}\) постійний. Якщо спочатку (тобто в\(t=0\)) всі атоми знаходяться в найнижчому стані:\(\Delta N(t=0)=-N\), то випливає з\(\PageIndex{12}\):\[\Delta N(t)=-N\left[\frac{A_{21}}{A_{21}+2 B_{12} W(\omega)}+\left(1-\frac{A_{21}}{A_{21}+2 B_{12} W(\omega)}\right) e^{-\left(A_{21}+2 B_{12} W(\omega)\right) t}\right] \nonumber \]
Приклад, де\(A_{21} / B_{12} W(\omega)=0.5\) показаний на рис\(\PageIndex{2}\). У нас завжди є\(\Delta N<0\), отже,\(N_{2}(t)<N_{1}(r)\) на всі часи\(t\). Тому система лише з двома рівнями не може мати інверсії населення.
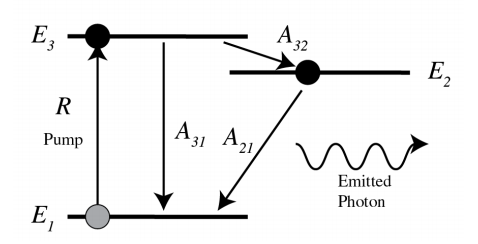
Спосіб досягнення інверсії населення рівнів 1 і 2 і, отже, посилення випромінювання з частотою\(\omega\) з\(\hbar \omega=E_{2}-E_{1}\) є використання більш атомних рівнів, наприклад трьох. На малюнку\(\PageIndex{3}\) основний стан - це стан 1 з двома верхніми рівнями 2 і 3 такими, що\(E_{1}<E_{2}<E_{3}\). Перехід інтересу все ще полягає в тому, що від рівня 2 до рівня 1. Спочатку майже всі атоми знаходяться в наземному стані 1. Потім атоми накачуються зі швидкістю\(R\) від рівня 1 безпосередньо до рівня 3. Перехід не\(3 \rightarrow 2\) є випромінювальним і має високу швидкість,\(A_{32}\) так що рівень 3 швидко спорожняється і тому\(N_{3}\) залишається малим. Стан 2 називають метастабільним станом, оскільки час перебування в метастабільному стані для кожного атома відносно тривалий. Тому його популяція має тенденцію до збільшення, що призводить до інверсії населення між метастабільним станом 2 та нижнім наземним станом 1 (яке безперервно знеселяється шляхом прокачування до найвищого рівня).
Зверніть увагу, що\(A_{31}\) має бути невеликим, тому що в іншому випадку рівень 1 швидко буде заповнений, за допомогою якого інверсія населення буде припинена. Цей ефект може бути використаний для отримання серії лазерних імпульсів як вихід, але небажаний для безперервної вихідної потужності.

Накачування може здійснюватися оптично, як описано, але енергія для передачі атомів від рівня 1 до рівня 3 також може подаватися електричним розрядом в газі або електричним струмом. Після того як прокачування досягла інверсії населення, спочатку світло не випромінюється. Так як же насправді запускається лазер? Lasing починається мимовільним випромінюванням. Спонтанно випромінювані фотони стимулюють випромінювання атомів на рівні 2 до розпаду до рівня 1, випромінюючи при цьому фотон енергії\(\hbar \omega\). Це стимульоване випромінювання відбувається у фазі з збуджуючим світлом і, отже, світло безперервно накопичується злагоджено, в той час як він підстрибує назад і вперед між дзеркалами резонатора. Одне з дзеркал трохи прозоре, і таким чином частина світла витікає з лазера.