7.2: Оптичний резонатор
- Page ID
- 78864
Ми зараз пояснимо роботу лазерів. Лазер складається з
- оптичний резонатор;
- підсилювальним середовищем.
У цьому розділі ми розглянемо резонатор. Його функція полягає в отриманні високої щільності світлової енергії та отримання контролю над довжинами хвиль випромінювання.
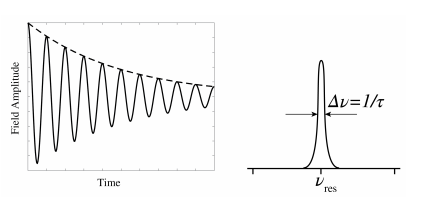
Резонатор, будь то механічний, як маятник, пружина або струна, або електричний, як ланцюг LRC, має одну або кілька резонансних частот\(\nu_{\text {res.}}\). Кожен резонатор має втрати, через які коливання поступово згасає, коли енергія не подається. Втрати викликають експоненціальне зменшення амплітуди коливання, як показано на малюнку\(\PageIndex{1}\). Тому коливання не є чисто монохроматичним, але має кінцеву смугу пропускання порядку\(\PageIndex{1}\),\(\Delta \nu \approx 1 / \tau\) як показано на малюнку, де\(\tau\) час, коли амплітуда коливання зменшилася до половини початкового значення.
Оптичний резонатор - це область, заповнена деяким матеріалом із показником заломлення,\(n\) обмеженою двома вирівняними, високо відбиваючими дзеркалами на відстані\(L\). Резонатор називається порожниною Фабри-Перо. Нехай по\(z\) осі порожнини вибирається -вісь так, як показано на рис. \(\PageIndex{2}\), І припустимо, що поперечні напрямки настільки великі, що світло можна вважати плоскою хвилею, що підстрибує назад і вперед вздовж\(z\) -осі між двома дзеркалами. \(\omega\)Дозволяти частоту і\(k_{0}=\omega / c\) число хвиль у вакуумі. Плоска хвиля, яка поширюється в\(z\) позитивному напрямку, задається:\[E(z)=A e^{i k_{0} n z}. \nonumber \]
Для дуже хороших дзеркал амплітуда залишається незмінною при відображеннях, тоді як фаза зазвичай змінюється на\(\pi\). Отже, після однієї поїздки в обидва кінці (тобто двох відображень) поле (\(\PageIndex{1}\)) є (можливі фазові зміни на дзеркалах складаються\(2 \pi\) і, отже, не мають ефекту):\[E(z)=A e^{2 i k_{0} n L} e^{i k_{0} n z} . \nonumber \] Високе поле накопичується, коли ця хвиля конструктивно заважає (\(\PageIndex{1}\)), тобто коли\[k_{0}=\frac{2 \pi m}{2 n L}, \quad \text { or } \quad \nu=\frac{k c}{2 \pi}=m \frac{c}{2 n L}, \nonumber \] для \(m=1,2, \ldots\). Отже, за умови дисперсії середовища можна знехтувати (\(n\)не залежить від частоти), резонансні частоти розділені за допомогою\[\Delta \nu_{f}=c /(2 n L), \nonumber \] якого є так званий вільний спектральний діапазон. Для газового лазера, який є\(1 \mathrm{~m}\) довгим, вільний спектральний діапазон приблизно\(150 \mathrm{MHz}\).

Припустимо, що порожнина\(100 \mathrm{~cm}\) довга і заповнена матеріалом з показником заломлення\(n=1\). Світло з видимою довжиною хвилі\(\lambda=500 \mathrm{~nm}\) відповідає номеру режиму,\(m=2 L / \lambda=4 \times 10^{6}\) а вільний спектральний діапазон дорівнює\(\Delta \nu_{f}=c /(2 L)=150 \mathrm{MHz}\).
Багаторазові відбиття лазерного світла всередині резонатора роблять довжину оптичного шляху дуже великою. Для спостерігача атомні джерела здаються на дуже великій відстані, а світло, що виходить з порожнини, нагадує плоску хвилю. Тому розбіжність променя обмежується не розміром джерела, а дифракцією через діафрагму вихідного дзеркала.
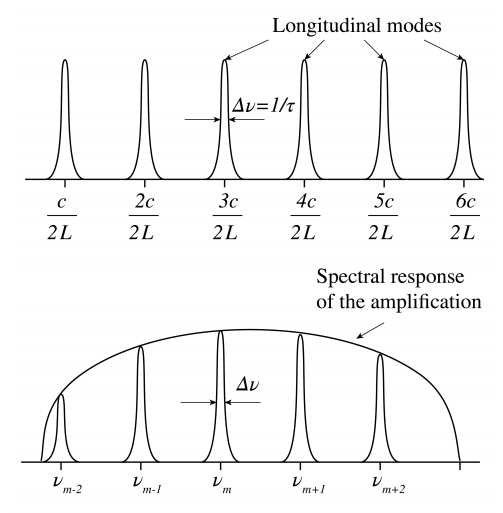
Через втрати, спричинені дзеркалами (які ніколи не відображаються ідеально) та поглинанням та розсіюванням світла, резонанси мають певну частотну ширину\(\Delta \nu\). Коли резонатор використовується як лазер, одному з дзеркал надається невелика пропускна здатність, щоб з'єднати лазерне світло. Це також сприяє втраті резонатора. Для компенсації всіх втрат порожнину повинна містити підсилює середовище. Завдяки посиленню ширини резонансної лінії всередині смуги пропускання підсилювача зменшуються до дуже гострих ліній, як показано на малюнку\(\PageIndex{3}\).