4.2: Сферична аберація

Ми почнемо з погляду на сферичну аберацію, що виникає в результаті відображення від сферичного дзеркала. Ми досі припускали, що паралельний промінь світла після відображення від сферичного дзеркала приходить до фокусу в точці, і що відстань фокусної точки від поверхні дзеркала становить половину радіуса кривизни дзеркала, як на малюнку IV.1:

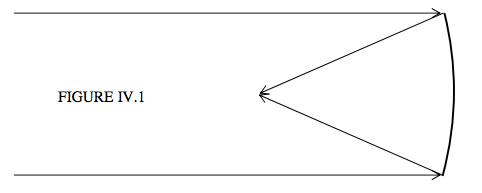
Приблизно це справедливо для дзеркала невеликої діафрагми («діафрагма» означає відношення діаметра до фокусної відстані). Однак це не стосується дзеркала з великою діафрагмою. На малюнку IV.2 я намалював напівсферичне дзеркало. Я припускаю, що є падаючий промінь світла (не намальований), що йде горизонтально зліва, і я намалював промені після відображення від дзеркала. (Деякі з променів будуть відображені вдруге від поверхні, перш ніж врешті-решт втекти, але я не намалював промені після другого відображення, тому що вони лише захаращують діаграму і не мають відношення до опису того, що я хочу описати. Ви можете бачити, що відбиті промені обмежені оболонкою, відомою як каустична крива, показана у вигляді пунктирно-червоної кривої на малюнку IV.2.

Чи можемо ми знайти рівняння цієї каустичної кривої?

Ми візьмемо центр кривизни дзеркала як початок O координат, і припустимо, що радіус кривизни дзеркала дорівнює$a$. Розглянемо пригоди променя світла, що йде паралельно горизонтальній$(x)$ осі і на висоті$h$ від неї. Рівняння вхідного світлового променя справедливе$y = h$, а рівняння дзеркальній поверхні є$x^2+y^2=a^2$. Трохи координатної геометрії дозволить нам визначити, що рівняння відбитого променя

$$y = \frac{h}{a^2-2h^2}\left[\left(2 \sqrt{a^2-h^2}x-a^2\right)\right], \label{eq:4.2.1}$$

і що він перетинає$x$ -вісь у точці C такий, що

$$OC = \frac{a^2}{2\sqrt{a^2-h^2}}. \label{eq:4.2.2}$$

Також зручно писати ці формули через кут$\theta$, який задається$h = a\sin \theta$. Після невеликої алгебри та застосування деяких тригонометричних тотожностей отримаємо

$$y = x \tan 2 \theta - \frac{a\sin\theta}{\cos2\theta}\label{eq:4.2.3}$$

для рівняння відбитого променя, і

$$OC = \frac{1}{2} a \sec \theta. \label{eq:4.2.4}$$

Ми можемо написати рівняння$\ref{eq:4.2.3}$ як

$$f(x,y;\theta)= x\tan2\theta-\frac{a\sin\theta}{\cos2\theta}-y=0.\label{eq:4.2.5}$$

З наших давно забутих, пожовклих і м'яких математичних нот ми нагадуємо, що щоб знайти рівняння до оболонки сімейства кривих форми$f(x,y;\theta)=0$, ми повинні усунути параметр$\theta$ з цього рівняння та рівняння$\frac{\partial f}{\partial \theta}=0$. Після ще деякої алгебри та більшого застосування тригонометричних ідентичностей ми виявляємо, що останнє рівняння приходить до

$$x=a\cos\theta.(\frac{3}{2}-\cos^2\theta).\label{eq:4.2.6}$$

Отже, все, що нам потрібно зробити, це усунути параметр$\theta$ з Рівняння$\ref{eq:4.2.3}$ і$\ref{eq:4.2.6}$, і це дасть нам$x , y$ рівняння каустичної кривої. Ці два рівняння є, по суті, параметричними рівняннями каустичної кривої. Тепер я не знаю, як легко було б усунути$\theta$. Оскільки рівняння$\ref{eq:4.2.6}$ є кубічним рівнянням$\cos \theta$, я підозрюю, що це може бути не особливо легко. Але (як це часто буває з двома параметричними рівняннями до кривої) ми можемо щасливо побудувати криву чисельно, без необхідності усунення параметра алгебраїчно. Таким чином, для побудови червоної кривої на малюнку IV.2 я варіювався$\theta$ від −90° до +90° і обчислював$x$ з Рівняння$\ref{eq:4.2.6}$, а потім обчислював$y$ з Рівняння$\ref{eq:4.2.3}$.

Щоб уникнути сферичної аберації, дзеркала телескопа можуть бути виконані в параболоїдальній формі. Можна показати, що падаючий промінь світла, що йде паралельно осі параболоїдного дзеркала, після відображення прийде в єдиний фокусний пункт, а саме в осередок параболи. Доказ цього наведено в розділі 2.4 глави 2 моїх приміток Небесної Механіки і там не повторюється. У цій главі також показано, що якщо відро рідини обертається навколо вертикальної осі, поверхня рідини прийме параболоїдальну форму, і там згадується про два застосування для виготовлення параболоїдальних дзеркал. В одному обертається чан з розплавленим склом і поступово охолоджується, поки скло не застигне в параболоїдальну форму. В іншому обертається ємність ртуті, поверхня ртуті приймає параболоїдальну форму, і цей рідкий параболоїд потім використовується як головне дзеркало відбиває телескопа. Хоча він може спостерігати лише близько до зеніту, деякі відмінні результати були отримані. Я не буду повторювати це тут, але ви, можливо, захочете посилатися на вищезгадані нотатки, оскільки це тут доречно.

Ця властивість (відбивається від поверхні параболи до єдиної фокусної точки) поширюється тільки на світло, що йде паралельно осі параболоїда. Отже, дзеркала параболоїдальних телескопів мають лише досить вузьке поле зору. Телескоп Шмідта використовує сферичне дзеркало (отже, велике поле зору), і, щоб уникнути сферичної аберації, перед дзеркалом встановлена коректорна пластина. Зазвичай сферичне дзеркало знаходиться на «нижньому кінці» трубки телескопа, а пластина коректора - на «верхньому кінці». Пластина коректора змушує світло, що надходить паралельно трубці телескопа, але на деякій відстані від осі трубки, трохи розходитися від осі, перш ніж дійти до сферичного дзеркала. Таким чином все вхідне світло, після відбиття від дзеркала, приходить до фокусу в одній точці.

Лінза також страждає від сферичної аберації, звичайно, але не піддається такому простому аналізу, як для сферичного дзеркала. Потрібно виконати детальне числове трасування променів, щоб знайти точну форму каустичної кривої для лінзи. Однак у розділі 1.4 глави 1 ми показали, що заломлення навіть на плоскій поверхні створює сферичну аберацію.

Можна здивуватися, враховуючи, що параболоїдальне дзеркало при використанні на осі не має сферичної аберації, чи лінза, зроблена з параболоїдальними поверхнями, також вільна від сферичної аберації. На жаль, це не так.

Однак можна сконструювати лінзу зі сферичними поверхнями, які мінімізують сферичну аберацію, шляхом відповідного вибору радіусів або кривизни поверхонь лінз. Це називається «згинання лінзи».

Наприклад, на малюнку IV.4 показано п'ять лінз, в яких я написав біля кожної поверхні його радіус кривизни в см. У чому випливає я припускаю, що лінза «тонка» в тому сенсі, що її товщина дуже мала в порівнянні з будь-якими іншими обговорюваними відстанями. Якщо показник заломлення дорівнює 1,6, кожна з цих лінз має фокусну відстань 20 см.

Охарактеризувати форму лінзи можна за допомогою її форм-фактора.

$$q=\frac{r_1+r_2}{r_1-r_2}\label{eq:4.2.7}$$

На малюнку IV.4 я написав коефіцієнт форми над кожною лінзою.

Для світла, що надходить горизонтально біля осі, фокусна відстань кожної з цих лінз становить 20 см. Однак світло, що надходить горизонтально на деякій відстані від осі, після проходження через лінзу падає трохи не дотягуючи 20 см. Ми можемо охарактеризувати сферичну аберацію кількістю, яку вона не вистачає. Припускаючи, що лінзи тонкі (в порівнянні з будь-якими іншими розглянутими відстанями) я розрахував недолік для променя світла, що надходить зліва на висоті 1 см від осі. Це показано на малюнку IV.5, на якому я намалював дефіцит (позначений «аберація» на малюнку) проти фактора форми$q$. Видно, що аберація найменше для коефіцієнта форми близько$q = −0.38$. Радіуси кривизн лінзи повинні задовольняти рівнянню$\ref{eq:4.2.7}$, а також$q = −0.38$

$$\frac{1}{f}=(n-1)\left(\frac{1}{r_1}-\frac{1}{r_2}\right), \label{eq:4.2.8}$$

так що при$f$ = 20 см і$q$ = −0,38 радіуси кривизни при найменшій сферичній аберації повинні бути$r_1$ = 17,4 см і$r_2$ = −38,7 см.

Звичайно, ви повинні правильно використовувати об'єктив! Якщо повернути його навколо, або якщо світло надходить праворуч, коефіцієнт форми становити+0,38, а сферична аберація не мінімальна. Майте на увазі, мінімум досить неглибокий, тому ви можете варіювати коефіцієнт форми на неабияку суму, не сильно збільшуючи сферичну аберацію.