1.6: Заломлення призмою

Last updated
Save as PDF

Page ID: 79052

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

На малюнку I.11 показана рівнобедрена призма кута\(\alpha\) і промінь світла, що проходить через неї.

Я намалював лише один промінь одного кольору. Для білого світла кольори будуть розсіяні, фіолетове світло відхиляється призмою більше, ніж червоне світло. Ми виберемо таку довжину хвилі, що показник заломлення призми\(n\). Відхилення D світла від його початкового напрямку дорівнює\(\theta_1 − \phi_1 + \theta_2 − \phi_2\). Я хочу уявити, тепер, якщо ми тримаємо падаючий промінь фіксованим і обертаємо призму, як відхилення змінюється з кутом падіння\(\theta_1\)? За геометрією\(\phi_2 = \alpha − \phi_1\), так що відхилення

\[ D = \theta_1 + \theta_2 -\alpha.\label{eq:1.6.1} \]

Застосуйте закон Снелла на кожній з двох заломлюючих поверхонь:

\[ \frac{\sin\theta_1}{\sin\phi_1} =n \quad \text{and} \quad \frac{\sin\theta_2}{\sin(\alpha - \phi_1)}=n, \label{eq:1.6.2a,b} \]

і усунути\(\phi_1\):

\[ \sin\theta_2 = \sin\alpha\sqrt{n^2-\sin^2\theta_1} -\cos\alpha\sin\theta_1. \label{eq:1.6.3} \]

Рівняння\(\ref{eq:1.6.1}\) і\(\ref{eq:1.6.3}\) дозволяють обчислити відхилення в залежності від кута падіння\(\theta_1\). Відхилення є найменше, коли світло проходить призму симетрично\(\theta_1 = \theta_2\), при цьому світло всередині призми потім паралельно основі. \(\theta_1 = \theta_2\)Введення рівняння показує, що мінімальне відхилення відбувається для кута падіння, заданого

\[ \sin \theta _ { 1 } = \frac { n \sin \alpha } { \sqrt { 2 ( 1 + \cos \alpha ) } } = n \sin \frac { 1 } { 2 } \alpha. \label{eq:1.6.4} \]

Кут мінімального відхилення\(D_{\text{min}}\) дорівнює\(2\theta_1 − \alpha\), де\(\theta_1\) задається рівнянням\(\ref{eq:1.6.4}\), і це призводить до наступного співвідношення між показником заломлення і кутом мінімального відхилення:

\[ n = \frac{\sin\frac{1}{2}(D_{\text{min}}+\alpha)}{\sin\frac{1}{2}\alpha}.\label{eq:1.6.5} \]

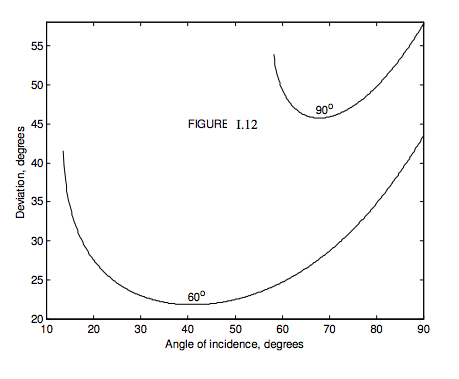
Особливий інтерес представляють призми з\(\alpha\) = 60 ° і\(\alpha\) = 90 °. Я намалював на малюнку I.12 відхилення від кута падіння для 60- і 90-градусних призм, використовуючи (з причин поясню)\(n = 1.31\), що приблизно є показником заломлення льоду. Для крижаної призми 60 ° кут мінімального відхилення становить 21 ° .8, а для крижаної призми 90 ° - 45 ° .7.

Сонячний ореол

Коли в атмосфері присутні гексагональні кристали льоду, сонячне світло розсіюється у всіх напрямках, відповідно до кутів падіння на різні кристали льоду (які можуть бути орієнтовані випадковим чином). Однак швидкість зміни відхилення з кутом падіння найменше близька до мінімального відхилення; отже набагато більше світла відхиляється на 21 ° .8, ніж через інші кути. Отже, ми бачимо ореол радіуса близько 22 ° навколо Сонця.

Побачивши боком на, гексагональний кристал прямокутний, а отже заломлення відбувається як би через призму 90 ° (рис. I.14):

Знову ж таки, швидкість зміни відхилення з кутом падіння є найменш близькою до мінімального відхилення, і, отже, ми можемо побачити ще один ореол, радіус близько 46 °. Для обох ореолов фіолетовий відхиляється більше, ніж червоний, і тому обидва ореола відтінені фіолетовим зовні і червоним зсередини.

1280 шт - Сонце з собаки_і_гало (24104827192). jpg — Рисунок: Сонячні ореоли з більшим і слабшим ореолом 46° та ореолом 22° з верхньою дотичною дугою. (CC BY 2.0; Фотобібліотека NOAA).