Skip to main content
LibreTexts - Ukrayinska

1.5: Відображення та заломлення

  1. Last updated
  2. Save as PDF
  • Page ID
    79051

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ми описали відображення і заломлення, але, звичайно, коли промінь світла стикається з інтерфейсом між двома прозорими носіями, частина його відбивається і частина заломлюється, і природно запитати, навіть під час раннього вступу до предмета, просто яка фракція відбивається і що фракція заломлюється. Відповідь на це досить складний, бо він залежить не тільки від кута падіння і від двох показників заломлення, але і від початкового стану поляризації падаючого світла; він переносить нас досить далеко в електромагнітну теорію і виходить за рамки цієї глави, якою покликана займатися значною мірою лише з геометрією відображення та заломлення. Однак, оскільки це закономірне питання, я можу дати явні формули для дробів, які відбиваються і заломлюються в тому випадку, коли падаюче світло неполяризоване.

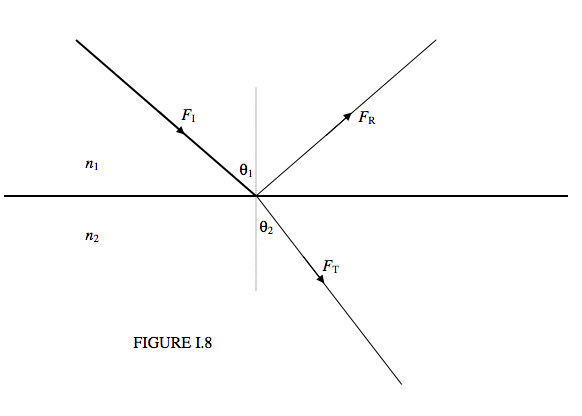
    На малюнку I.8 показаний падаючий промінь щільності потоку енергії (W m −2 в нормі до напрямку поширення), що\(F_I\) надходить на межу між середовищами індексів\(n_1\) і\(n_2\). Згодом він ділиться на відбитий промінь щільності потоку\(F_R\) і переданий промінь щільності потоку\(F_T\). Дроби, що передаються і відображені (\(t\)і\(r\))

    \[ t = \frac{F_T}{F_I} = 2n_1n_2 \cos\theta_1\cos\theta_2\left( \frac{1}{(n_1\cos\theta_1+n_2\cos\theta_2)^2} + \frac{1}{(n_1\cos\theta_1+n_2\cos\theta_1)^2}\right) \label{eq:1.5.1} \]

    і

    \[ r = \frac{F_T}{F_I} =\frac{1}{2}\left[\left( \frac{n_1\cos\theta_1-n_2\cos\theta_2}{(n_1\cos\theta_1+n_2\cos\theta_2)^2}\right)^2 + \left(\frac{n_1\cos\theta_1-n_2\cos\theta_1}{(n_1\cos\theta_1+n_2\cos\theta_1)^2}\right)^2\right] \label{eq:1.5.2} \]

    Тут кути та індекси пов'язані через закон Снелла, рівняння 1.3.2. Якщо у вас є енергія, покажіть, що сума їх дорівнює 1. І передані, і відбиті промені частково плоскі поляризовані. Якщо кут падіння і показник заломлення такі, що передаються і відбиті промені перпендикулярні один одному, відбитий промінь повністю плоский поляризований — але такі деталі не повинні турбувати нас у цій главі.

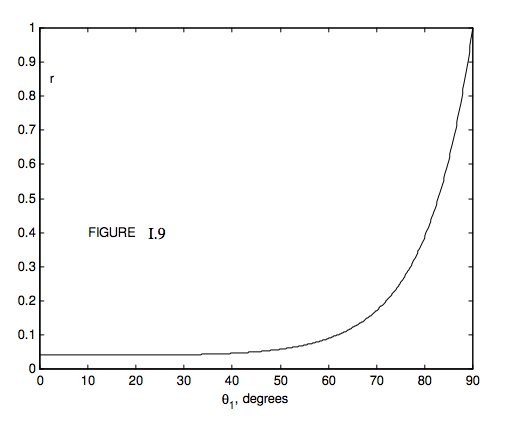
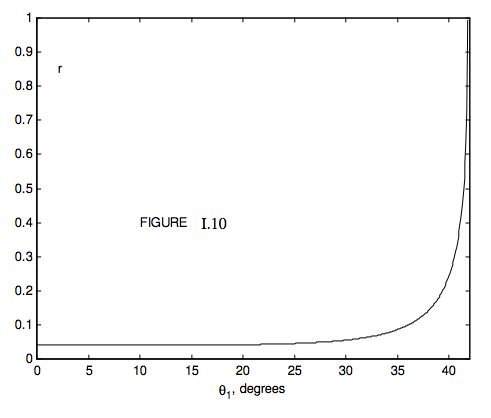
    На малюнку I.9 показано коефіцієнт відбиття як функцію кута падіння для неполяризованого падаючого світла з\(n_1 = 1.0\) і\(n_2 = 1.5\) (наприклад, склом). Так як\(n_2 > n_1\), ми маємо зовнішнє відображення. Ми бачимо, що при кутах падіння менше приблизно 45 градусів відбивається дуже мало світла, але після цього коефіцієнт відбиття швидко зростає з кутом падіння, наближаючись до одиниці як\( \theta_1\) → 90 ° (випас випасу). Якщо\(n_1 = 1.5\) і\(n_2 = 1.0\), то маємо внутрішнє відображення, а коефіцієнт відбиття для цього випадку показаний на малюнку I.10. При внутрішніх кутах падіння менше приблизно 35 ° мало світла відбивається, решта передається. Після цього коефіцієнт відбиття швидко зростає, поки внутрішній кут падіння не\(\theta_1\) наближається до критичного кута\(C\), заданого

    \[ \sin C = \frac{n_2}{n_1},\label{eq:1.5.3} \]

    Це відповідає куту сходження в 90 °. Для кутів падіння, більших за цей, світло повністю внутрішньо відбивається. Для скла з показником заломлення 1.5 критичний кут становить 41 ° .2, так що світло повністю внутрішньо відбивається всередині призми 45 °, наприклад, використовується в біноклі.