9.2: Правило трапеції
- Page ID
- 79655
Правило трапеції є простим продовженням правила інтеграції середньої точки. Замість обчислення площі послідовності прямокутників обчислюємо площу послідовності трапецій, як показано на рис. \(\PageIndex{1}\). Як і раніше, ми ділимо область інтеграції на\(N\) рівні сегменти; однак зараз ми розглянемо кінцеві точки цих сегментів, а не їх середні точки. Це набір\(N+1\) позицій\(\{x_0, \dots x_{N}\}\), таких, що
\[x_n = a + n\, \Delta x ,\quad \Delta x \equiv \frac{b-a}{N}.\]
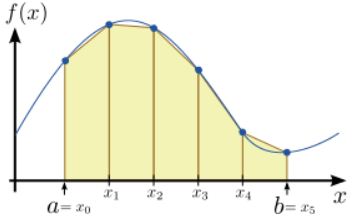
Зверніть увагу, що\(a = x_0\) і\(b=x_{N}\). Використовуючи звичну формулу для площі кожної трапеції, ми можемо наблизити інтеграл як
\[\begin{align}\mathcal{I}^{\mathrm{trapz}} &= \sum_{n=0}^{N-1} \Delta x \left(\frac{f(x_n) + f(x_{n+1})}{2}\right) \\ &= \Delta x \left[\left(\frac{f(x_0) + f(x_1)}{2}\right)+ \left(\frac{f(x_1) + f(x_2)}{2}\right) + \cdots + \left(\frac{f(x_{N-1}) + f(x_{N})}{2}\right)\right] \\ &= \Delta x \left[\frac{f(x_0)}{2} + \left(\sum_{n=1}^{N-1} f(x_n)\right) + \frac{f(x_{N})}{2}\right].\end{align}\]
9.2.1 Реалізація правила трапеції на Python
У Scipy правило трапеції реалізується функцією trapz. Зазвичай він приймає два аргументи масиву, y та x; тоді виклик функції trapz (y, x) повертає оцінку правила трапеції для\(\int y \;dx\), використовуючи елементи x як точки дискретизації, а елементи y як значення integrand at ці точки.
Примітка
Ma tlab Примітка про сумісність: Будьте обережні з порядком входів! Для функції Scipy це trapz (y, x). Для однойменної функції Matlab входи подаються в протилежному порядку, як trapz (x, y).
Зверніть увагу, що точки дискретизації в x не повинні бути однаково розташовані. Крім того, ви можете викликати функцію як trapz (y, dx=s); це виконує числове інтегрування, припускаючи однаково розташовані точки дискретизації, з інтервалом s.
Ось приклад використання trapz для оцінки інтеграла\(\int_0^\infty \exp(-x^2) dx = 1\):
>>> from scipy import * >>> x = linspace(0,10,25) >>> y = exp(-x) >>> t = trapz(y,x) >>> print(t) 1.01437984777
9.2.2 Числова помилка для правила трапеції
З візуального порівняння рис. 9.1.1 (для правила середньої точки) і рис. \(\PageIndex{1}\)(для правила трапеції) у нас може виникнути спокуса зробити висновок, що правило трапеції має бути більш точним. Перш ніж перейти до цього висновку, однак, давайте зробимо фактичний розрахунок числової помилки. Це схоже на наш вище розрахунок числової помилки правила середньої точки. Для правила трапеції, однак, зручно вважати пару сусідніх відрізків, які лежать між трьома точками дискретизації\(\left\{x_{n-1}, x_n, x_{n+1}\right\}\).
Як і раніше, ми виконуємо розширення\(f(x)\) Тейлора поблизу\(x_{n}\):
\[f(x) = f(x_n) + f'(x_n) (x-x_n) + \frac{f''(x_n)}{2} (x-x_n)^2 + \frac{f'''(x_n)}{6} (x-x_n)^3 + \cdots \]
Якщо ми інтегруємо\(f(x)\) від\(x_{n-1}\) до\(x_{n+1}\), результат
\[\begin{align} \mathcal{I}_n & \equiv \int_{x_n - \Delta x}^{x_n + \Delta x} f(x) dx \\ &= \; 2 f(x_n) \Delta x \;\;+\; f'(x_n) \int_{x_n - \Delta x}^{x_n + \Delta x} (x-x_n) dx \; +\; \frac{f''(x_n)}{2} \int_{x_n - \Delta x}^{x_n + \Delta x} (x-x_n)^2 dx \; +\; \cdots \end{align}\]
Як і раніше, кожен інший термін з правого боку інтегрується в нуль. Нам залишилося
\[\mathcal{I}_n \; = \; 2 f(x_n) \Delta x \;+\; \frac{f''(x_n)}{3} \Delta x^3 + O(\Delta x^5) \;+\; \cdots \]
Це доводиться порівнювати з оцінкою, виробленою правилом трапеції, яка
\[\mathcal{I}_n^{\mathrm{(trapz)}} = \Delta x \left[ \frac{f(x_{n-1})}{2} + f(x_n) + \frac{f(x_{n+1})}{2}\right].\]
Якщо ми Taylor розширити перший і останній терміни вищевказаного виразу навколо\(x_{n}\), результат буде:
\[\begin{align} \mathcal{I}_n^{\mathrm{(trapz)}} & = \frac{\Delta x}{2} \left[f(x_n) - f'(x_n) \Delta x + \frac{f''(x_n)}{2} \Delta x^2 - \frac{f'''(x_n)}{6} \Delta x^3 + \frac{f''''(x_n)}{24} \Delta x^4 + O(\Delta x^4)\right] \\ &\quad + \;\;\Delta x \; f(x_n) \\ &\quad + \frac{\Delta x}{2} \left[f(x_n) + f'(x_n) \Delta x + \frac{f''(x_n)}{2} \Delta x^2 + \frac{f'''(x_n)}{6} \Delta x^3 + \frac{f''''(x_n)}{24} \Delta x^4 + O(\Delta x^4)\right] \\ & = 2 f(x_n) \Delta x + \frac{f''(x_n)}{2} \Delta x^3 + O(\Delta x^5). \end{align}\]
Отже, числова помилка інтеграції над цією парою сегментів
\[\mathcal{E}_n \;\equiv\; \left|\mathcal{I}_n - \mathcal{I}_n^{\mathrm{trapz}}\right| \;=\; \frac{|f''(x_n)|}{6} \Delta x^3 \;\sim\; O\left(\frac{1}{N^3}\right).\]
І загальна числова помилка йде як
\[\mathcal{E}_{\mathrm{total}} \sim O\left(\frac{1}{N^2}\right),\]
яке таке ж масштабування, як правило середньої точки! Незважаючи на наші очікування, правило трапеції насправді не є поліпшенням порівняно з правилом середньої точки, що стосується числової точності.
