14.6: Проблеми

1. Якщо радіоактивна речовина має період напіврозпаду один рік, чи означає це, що воно буде повністю розпадатися через два роки? Поясніть.

2. Яка ймовірність прокатки пари кубиків і отримання «зміїних очей», тобто обидва кубика придумують з них?

3. Проблема 3 була видалена.

4. Проблема 4 була видалена.

5. Зверніться до розподілу ймовірностей зросту людей на малюнку f на сторінці 828.
(а) Показати, що графік правильно нормований.
(b) Оцінити частку населення, що має висоту від 140 до 150 см. (Перевірка відповіді доступна на сайті lightandmatter.com)

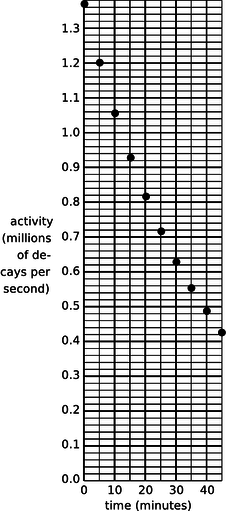
a/ Задача 6.

6. (а) Ядерний фізик вивчає ядерну реакцію, викликану в експерименті з прискорювачем, при цьому пучок іонів з прискорювача вражає тонку металеву фольгу і викликає ядерні реакції, коли ядро з одного з іонів пучка потрапляє в одне з ядер в ціль. Після того, як експеримент тривав протягом декількох годин, було вироблено кілька мільярдів радіоактивних атомів, вбудованих в ціль. Вона не знає, які ядра виробляються, але вона підозрює, що вони є ізотопом якогось важкого елемента, такого як Pb, Bi, Fr або U. після одного такого експерименту вона виймає цільову фольгу з прискорювача, наклеює її перед детектором, вимірює активність кожні 5 хв і робить графік (малюнок). Ізотопи, на її думку, могли бути вироблені:

ізотопу	період напіврозпаду (хвилин)
^211 Пб	36.1
^214 Пб	26.8
214 Бі	19.7
^223 Пт	21.8
^239 У.О.	23.5

Який з них це?
(б) Вирішивши, що початкові експериментальні умови виробляють один специфічний ізотоп, вона тепер намагається використовувати пучки іонів, що рухаються з кількома різними швидкостями, що може викликати різні реакції. Наступна таблиця дає активність мішені 10, 20 і 30 хвилин після закінчення експерименту, для трьох різних швидкостей іонів.

	активність (мільйони розпадів/с) після...
	10 хв	20 хв	30 хв
швидкість першого іона	1.933	0.832	0,382
друга швидкість іонів	1.200	0,545	0,248
третя швидкість іонів	7.211	1.296	0,248

Оскільки підраховується така велика кількість розпадів, припустимо, що дані лише неточні через округлення при записі таблиці. Які узгоджуються з виробництвом одного ізотопу, а які означають, що створювалося більше одного ізотопу?

7. Придумайте метод експериментального тестування гіпотези про те, що шанс гравця на перемогу в кістки не залежить від її попереднього рекорду виграшів і втрат. Якщо ви не посилаєтеся на визначення статистичної незалежності, то ви не запропонували тест.

8. Людина з зав'язаними очима стріляє з гармати по круговій цілі радіусу$b$, і йому дозволяється продовжувати стрільбу, поки постріл фактично не потрапить в неї. Будь-яка частина цілі з однаковою ймовірністю отримає удар. Вимірюємо випадкову відстань$r$ від центру кола до місця, куди потрапила куля.
(а) Показати, що розподіл ймовірності$r$ повинен бути тієї форми$D(r)=kr$, де$k$ є деяка константа. (Звичайно, у нас є$D(r)=0$ для$r>b$.)
(b) Визначити$k$, вимагаючи$D$ належним чином нормалізувати. (Перевірка відповіді доступна на сайті lightandmatter.com)

(c) Знайти середнє значення$r$. (Перевірка відповіді доступна на lightandmatter.com)

(d) Інтерпретація вашого результату з частини c, як це порівнюється з$b/2$? Чи має це сенс? Поясніть.

9. Нам дано деякі атоми певного радіоактивного ізотопу, з періодом напіврозпаду$t_{1/2}$. Ми вибираємо один атом навмання і спостерігаємо за ним протягом одного періоду напіврозпаду, починаючи з нульового часу. Якщо він розпадається протягом цього періоду напіврозпаду, ми фіксуємо$t$ час, коли відбувся розпад. Якщо це не так, ми скидаємо годинник до нуля і продовжуємо намагатися, поки не отримаємо атом, який співпрацює. Кінцевим результатом є час$0\le t\le t_{1/2}$, з розподілом, який виглядає як звичайна експоненціальна крива розпаду, але з відрубаним хвостом.
(a) Знайдіть розподіл з$D(t)$ належною нормалізацією. (Перевірка відповіді доступна на сайті lightandmatter.com)

(б) Знайти середнє значення$t$. (Перевірка відповіді доступна на lightandmatter.com)

(c) Інтерпретація вашого результату з частини b, як це порівнюється з$t_{1/2}/2$? Чи має це сенс? Поясніть.

10. Швидкість$v$, атома в ідеальному газі має ймовірність розподілу форми$D(v) = bve^{-cv^2}$, де$0\le v \lt \infty$,$c$ відноситься до температури, і$b$ визначається нормалізацією.
(а) Намалюйте розподіл.
(б) Знайти з$b$ точки зору$c$. (Перевірка відповіді доступна на сайті lightandmatter.com)

(c) Знайти середню швидкість з точки зору$c$, усунення$b$. (Не намагайтеся робити невизначений інтеграл, тому що це не може бути зроблено в закритому вигляді. Відповідний певний інтеграл можна знайти в таблицях або зробити за допомогою комп'ютерного програмного забезпечення.) (Перевірка відповіді доступна на сайті lightandmatter.com)

11. Весь гелій на землі відбувається від розпаду природних важких радіоактивних елементів, таких як уран. Кожна альфа-частинка, яка випромінюється, закінчує претендувати на два електрони, що робить її атомом гелію. Якщо вихідний$^{238}\text{U}$ атом знаходиться в твердій породі (на відміну від розплавлених областей землі), атоми Він не в змозі дифузійно виходити з породи. Ця проблема передбачає датування породи з використанням відомих властивостей розпаду урану 238. Припустимо, геолог знаходить зразок затверділої лави, розплавляє її в печі, і виявляє, що в ній міститься 1230 мг урану і 2,3 мг гелію. $^{238}\text{U}$розпадається за рахунок альфа-викиду, з періодом напіврозпаду$4.5\times10^9$ років. Наступний ланцюг альфа- і електронного (бета) розпаду передбачає набагато більш короткі періоди напіврозпаду, і закінчується в стабільному ядрі$^{206}\text{Pb}$. Майже весь природний уран є$^{238}\text{U}$, і хімічний склад цієї породи свідчить про те, що не було задіяних ланцюгів розпаду, крім ланцюгів розпаду$^{238}\text{U}$.
(а) Скільки альф викидається на ланцюг розпаду? [Підказка: Використовуйте збереження маси.]
(b) Скільки електронів випромінюється на ланцюг розпаду? [Підказка: Використовуйте збереження заряду.]
(c) Скільки часу пройшло з тих пір, як лава спочатку затверділа? (Перевірка відповіді доступна на сайті lightandmatter.com)

12. Коли світло відбивається від дзеркала, можливо, тільки 80% енергії повертається назад. Можна спробувати пояснити це двома різними способами: (1) 80% фотонів відбиваються, або (2) відбиваються всі фотони, але кожен втрачає 20% своєї енергії. Виходячи з ваших повсякденних знань про дзеркала, як ви можете сказати, яке тлумачення є правильним? [На основі завдання з фізики PSSC.]

13. Припустимо, ми хочемо побудувати електронний датчик освітленості за допомогою такого апарату, як описаний в розділі про фотоефект. Як би його здатність виявляти різні частини спектра залежатиме від типу металу, що використовується в обкладинках конденсатора?

14. Фотоелектричний ефект може відбуватися не тільки для металевих катодів, але і для будь-якої речовини, включаючи живу тканину. Іонізація молекул ДНК може викликати рак або вроджені дефекти. Якщо енергія, необхідна для іонізації ДНК, знаходиться на тому ж порядку, що і енергія, необхідна для створення фотоелектричного ефекту в металі, який з наступних типів електромагнітних хвиль може становити таку небезпеку? Поясніть.

Хвилі 60 Гц від ліній електропередач

100 МГц FM-радіо

мікрохвильові печі з мікрохвильової печі

видиме світло

ультрафіолетове світло

рентгенівські промені

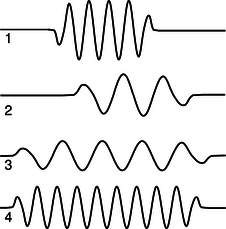
b/Задача 15.

15. (а) Ранг порядку фотони відповідно до їх довжини хвиль, частот і енергій. Якщо два рівні, скажіть так. Поясніть всі свої відповіді.
(b) Фотон 3 випромінювався атомом ксенону, що переходить від другого стану за низькою енергією до стану найнижчої енергії. Які з фотонів 1, 2 і 4 здатні збуджувати атом ксенону від його стану найнижчої енергії до стану другого за низькою енергією? Поясніть.

c/Задача 16.

16. Яка фігура може бути електроном, що прискорюється, коли він рухається вправо? Поясніть.

17. Промінь проектора потужністю 100 Вт охоплює площу,$1\ \text{m}\times1\ \text{m}$ коли він потрапляє на екран на відстань 3 м. Оцініть кількість фотонів, які знаходяться в польоті в будь-який момент часу. (Оскільки це лише оцінка, ми можемо ігнорувати той факт, що промінь не паралельний.) (Перевірка відповіді доступна на сайті lightandmatter.com)

18. У фотоелектричному ефекті електрони спостерігаються практично без затримки часу ($\sim10$нс), навіть коли джерело світла дуже слабкий. (Слабке джерело світла, однак, виробляє лише невелику кількість викинутих електронів.) Мета цієї проблеми - показати, що відсутність значної затримки часу суперечило класичній хвильовій теорії світла, тому протягом усієї цієї проблеми слід поставити себе на місце класичного фізика і робити вигляд, що ви взагалі не знаєте про фотони. У той час вважалося, що електрон може мати радіус порядку$10^{-15}$ m. (Останні експерименти показали, що якщо електрон взагалі має будь-який кінцевий розмір, він набагато менший.)
(а) Оцініть потужність, яка буде просочена одним електроном у пучку світла з інтенсивністю 1$\text{mW}/\text{m}^2$. (Перевірка відповіді доступна на lightandmatter.com)
(b) Енергія$E_s$, необхідна для виходу електрона через поверхню катода, знаходиться на порядку$10^{-19}$ J. Знайдіть, скільки часу потрібно електрону, щоб поглинути цю кількість енергії, і поясніть, чому ваш результат є сильним докази того, що з класичною теорією щось не так. (Перевірка відповіді доступна на сайті lightandmatter.com)

19. У телевізорі, припустимо, електрони прискорюються від спокою через різницю напруг$10^4$ V. Яка їх кінцева довжина хвилі? (Перевірка відповіді доступна на сайті lightandmatter.com)

20. Використовуйте принцип невизначеності Гейзенберга для оцінки мінімальної швидкості протона або нейтрона в$^{208}\text{Pb}$ ядрі, який має діаметр близько 13 фм (1$10^{-15}$ fm = m). Припустимо, що швидкість нерелятивістська, а потім перевірте в кінці, чи виправдано це припущення. (Перевірка відповіді доступна на сайті lightandmatter.com)

21. Знайдіть енергію частинки в одновимірній коробці довжини$L$, виражаючи свій результат через масу частинки$m$, кількість піків і долин$n$ у хвильовій функції та фундаментальних констант.$L$ (Перевірка відповіді доступна на сайті lightandmatter.com)

22. Вільний електрон, який сприяє струму в омічному матеріалі, зазвичай має швидкість$10^5$ м/с (набагато більшу, ніж швидкість дрейфу).
(а) Оцініть його довжину хвилі де Броля, в нм. (Перевірка відповіді доступна на сайті lightandmatter.com)
(b) Якщо мікросхема пам'яті комп'ютера містить$10^8$ електричні ланцюги в$\text{cm}^2$ області 1, оцініть лінійний розмір, в нм, однієї такої схеми. (Перевірка відповідей доступна на lightandmatter.com)
(c) На основі ваших відповідей з частин a і b, чи потрібно інженера-електрику, проектуючи такий чіп, турбуватися про хвильові ефекти, такі як дифракція?
(d) Оцініть максимальну кількість електричних ланцюгів, які можуть поміститися на$\text{cm}^2$ комп'ютерному чіпі 1, перш ніж квантово-механічні ефекти стануть важливими.

23. У класичній механіці енергію взаємодії форми$U(x)=\frac{1}{2}kx^2$ дає гармонійний генератор: частка рухається вперед і назад з частотою$\omega=\sqrt{k/m}$. Ця форма для часто$U(x)$ є хорошим наближенням для окремого атома в твердому тілі, який може вібрувати навколо свого положення рівноваги при$x=0$. (Для простоти ми обмежуємо наше лікування одним виміром, і ми розглядаємо атом як єдину частинку, а не як ядро, оточене електронами). Атом, однак, слід обробляти квантово-механічно, а не класично. Він буде мати хвильову функцію. Ми очікуємо, що ця хвильова функція матиме один або кілька піків у класично дозволеному регіоні, і ми очікуємо, що вона буде хвоста в класично заборонених регіонах праворуч і ліворуч. Так як форма парабола, а не серія плоских сходинок як на малюнку м на стор. 869, хвиляста частина посередині не буде синусоїдою, а хвости не будуть експоненціальними.$U(x)$
(а) Показати, що існує рішення рівняння Шредінгера форми

$$\begin{equation*} \Psi(x)=e^{-bx^2} , \end{equation*}$$

і відносяться$b$ до$k$$m$, і$\hbar$. Для цього обчисліть другу похідну, підключіть результат до рівняння Шредінгера, а потім знайдіть, яке значення$b$ зробить рівняння дійсним для всіх значень$x$. Ця хвильова функція виявляється заземленим станом. Зверніть увагу, що ця хвильова функція неправильно нормалізована - не турбуйтеся про це. (Перевірка відповіді доступна на lightandmatter.com)
(б) Намалюйте графік, що показує, як виглядає ця хвильова функція.
(c) Давайте інтерпретуємо$b$. Якби ви змінили$b$, як би хвильова функція виглядала інакше? Продемонструйте, накидаючи два графіки, один для меншого значення$b$, а другий для більшого значення.
(d) Зробити$k$ більше означає зробити атом більш щільно пов'язаним. Математично, що відбувається зі значенням$b$ у вашому результаті з частини а, якщо ви робите$k$ більше? Чи має це сенс фізично, коли ви порівнюєте з частиною c?

24. (a) Шкала відстані показана під хвильовими функціями та щільністю ймовірностей, проілюстрованих на малюнку e на сторінці 882. Порівняйте це з оцінкою порядку величини, отриманою в підрозділі 13.4.4 для радіуса,$r$ при якому хвильова функція починає відступати. Чи була кошторис на потрібному порядку?
(b) Хоча ми зазвичай говоримо, що Місяць обертається навколо Землі, насправді вони обидва обертаються навколо свого загального центру мас, який знаходиться нижче земної поверхні, але не в її центрі. Те ж саме стосується атома водню. Центр маси лежить всередині протона, або поза ним?

d/Задача 25.

25. На малюнку показано вісім можливих способів, за допомогою яких електрон в атомі водню міг впасти з вищого енергетичного стану в стан нижчої енергії, вивільняючи різницю в енергії як фотон. З цих восьми переходів тільки D, E і F виробляють фотони з довжинами хвиль у видимому спектрі.
(a) Який із видимих переходів був би найближчим до фіолетового кінця спектра, а який був би найближчим до червоного кінця? Поясніть.
(b) У якій частині електромагнітного спектра будуть лежати фотони з переходів A, B та C? А як щодо G і H? Поясніть.
(c) Чи існує верхня межа довжин хвиль, які можуть бути випущені атомом водню, що переходить з одного пов'язаного стану в інший пов'язаний стан? Чи є нижня межа? Поясніть.

26. Знайдіть рівняння довжини хвилі фотона, що випромінюється, коли електрон в атомі водню здійснює перехід від енергетичного рівня$n_1$ до рівня$n_2$. (Перевірка відповіді доступна на сайті lightandmatter.com)

27. Оцініть кутовий імпульс спінінгового баскетболу, в одиницях$\hbar$. Поясніть, як цей результат пов'язаний з принципом відповідності.

28. Припустимо, що кінетична енергія електрона$n=1$ стан атома водню знаходиться на тому ж порядку, що і абсолютне значення його загальної енергії, і оцініть типовну швидкість, з якою він буде рухатися. (Він насправді не може мати єдиної певної швидкості, тому що його кінетична і взаємодія енергія компромісуються на різних відстанях від протона, але це лише приблизна оцінка типової швидкості.) Виходячи з цієї швидкості, чи були ми виправдані, припускаючи, що електрон можна описати нерелятивістично?

29. Перед квантовою теорією експериментатори відзначали, що в багатьох випадках вони знаходять три лінії в спектрі одного і того ж атома, які задовольняли такому загадковому правилу:$1/\lambda_1=1/\lambda_2+1/\lambda_3$. Поясніть, чому це станеться. Не використовуйте міркування, які працюють лише для водню — такі комбінації трапляються в спектрах усіх елементів. [Підказка: Повторюйте рівняння з точки зору енергій фотонів.]

30. Хвильова функція електрона в основному стані атома водню дорівнює

$$\begin{equation*} \Psi = \pi^{-1/2} a^{-3/2} e^{-r/a} , \end{equation*}$$

де$r$ - відстань від протона, а$a=5.3\times10^{-11}$ m - константа, яка задає розмір хвилі.
(а) Обчислити символічно, не забиваючи числа, ймовірність того, що в будь-який момент електрон знаходиться всередині протона. Припустимо, що протон - це сфера з радіусом$b=0.5$ fm. [Підказка: Чи має значення, якщо ви підключите$r=0$ або$r=b$ в рівнянні для хвильової функції?] (Перевірка відповіді доступна на сайті lightandmatter.com)
(б) Обчисліть ймовірність чисельно. (Перевірка відповіді доступна на lightandmatter.com)
(c) Виходячи з рівняння для хвильової функції, чи справедливо думати про атом водню як про кінцевий розмір? Можна$a$ трактувати як розмір атома, за яким немає нічого? Або є якась межа на те, наскільки далеко електрон може знаходитися від протона?

31. Використовуйте фізичні міркування, щоб пояснити, як рівняння енергетичних рівнів водню,

$$\begin{equation*} E_n = -\frac{mk^2e^4}{2\hbar^2}\cdot\frac{1}{n^2} , \end{equation*}$$

слід узагальнити до випадку атома з атомним номером$Z$, у якого були видалені всі його електрони, крім одного.

32. Мюон - це субатомна частинка, яка діє точно так само, як електрон, за винятком того, що її маса в 207 разів більше. Мюони можуть створюватися космічними променями, і може статися, що один з електронів атома зміщується мюоном, утворюючи мюонічний атом. Якщо це відбувається з атомом водню, отримана система складається просто з протона плюс мюона.
(а) Виходячи з результатів розділу 13.4.4, як би розмір мюонічного атома водню в його основному стані порівнювався з розміром нормального атома?
(b) Якби ви шукали мюонічні атоми на сонці або в земній атмосфері методом спектроскопії, в якій частині електромагнітного спектра ви очікували б знайти лінії поглинання?

33. Фотон стикається з електроном і відскакує від зіткнення на 180 градусів, тобто повертаючись назад по шляху, по якому він прийшов. Відскок фотон має різну енергію, а значить і різну частоту і довжину хвилі. Показати, що на основі збереження енергії і імпульсу різниця між початковою і кінцевою довжинами хвиль фотона повинна бути$2h/mc$, де$m$ маса електрона. Експериментальна перевірка цього типу поведінки «пул-м'яч» Артуром Комптоном у 1923 році була прийнята як остаточний доказ природи частинок світла. Зауважте, що ми не робимо жодних нерелятивістських наближень. Щоб алгебра була простою, вам слід використовувати природні одиниці - насправді, це гарна ідея використовувати навіть більш-природні-ніж природні одиниці, в яких ми маємо не просто$h=1$,$c=1$ але й, і$m=1$ для маси електрона. Ви також, ймовірно, захочете використовувати релятивістські відносини$E^2-p^2=m^2$, які стають$E^2-p^2=1$ для енергії і імпульсу електрона в цих одиницях.

34. Узагальнити результат задачі 33 до випадку, коли фотон відскакує під кутом, відмінним від 180° відносно його початкового напрямку руху.

35. На сторінці 869 ми вивели вираз ймовірності того, що частинка буде тунелювати через прямокутний бар'єр, тобто область, в якій енергія взаємодії$U(x)$ має графік, схожий на прямокутник. Узагальніть це до бар'єру будь-якої форми. [Підказки: Спочатку спробуйте узагальнити два прямокутні бар'єри поспіль, а потім використайте ряд прямокутних бар'єрів, щоб наблизити фактичну криву довільної функції$U(x)$. Зверніть увагу, що ширина і висота бар'єру в початковому рівнянні відбуваються таким чином, що все, що має значення, - це площа під$x$ кривою$U$ -проти-. Покажіть, що це все ще вірно для ряду прямокутних бар'єрів, і узагальнити за допомогою інтеграла.] Якби ви зробили цей розрахунок в 1930-х роках, ви могли б стати відомим фізиком.

36. Показати, що хвильова функція, задана в задачі 30, правильно нормалізована.

37. Показати, що хвильова функція виду$\Psi = e^{by} \sin ax$ є можливим розв'язком рівняння Шредінгера в двох вимірах, з постійним потенціалом. Чи можемо ми сказати, чи буде це стосуватися класично дозволеного регіону, чи класично забороненого?

38. Знайти енергетичні рівні частинки в тривимірній прямокутній коробці зі сторонами довжини$a$$b$, і$c$. (Перевірка відповіді доступна на сайті lightandmatter.com)

39. Americium-241 - штучний ізотоп, який використовується в детекторах диму. Він піддається альфа-розпаду, з періодом напіврозпаду 432 роки. Як обговорювалося в прикладі 18 на сторінці 870, альфа-розпад можна розуміти як процес тунелювання, і хоча бар'єр не має прямокутної форми, рівняння ймовірності тунелювання на сторінці 870 все ще можна використовувати як приблизний посібник для нашого мислення. Для америцію-241 ймовірність тунелювання становить близько$1\times10^{-29}$. Припустимо, що це ядро повинно було розпастися, виділяючи тритієве (гелій-3) ядро замість альфа-частинки (гелій-4). Оцініть відповідну ймовірність тунелювання, припускаючи, що загальна енергія$E$ залишається колишньою. Ця більш висока ймовірність суперечить емпіричному спостереженню, що це ядро не спостерігається розпаду викидом тритію з будь-якою значною ймовірністю, і загалом емісія тритію майже невідома в природі; це головним чином тому, що ядро тритію набагато менш стабільне, ніж ядро гелію-4, а різниця в енергії зв'язування зменшує енергію, доступну для розпаду.

40. Наскільки нам відомо, маса фотона дорівнює нулю. Однак експериментами неможливо довести, що що-небудь дорівнює нулю; все, що ми можемо зробити, це поставити верхню межу числа. Станом на 2008 рік найкраща експериментальна верхня межа по масі фотона становить близько$1\times 10^{-52}$ кг. Припустимо, що маса фотона насправді не дорівнює нулю, і що значення знаходиться у верхній частині діапазону, що відповідає справжнім експериментальним доказам. У цьому випадку$c$ відбувається в теорії відносності більше не буде інтерпретуватися як швидкість світла. Як і у випадку з матеріальними частинками, швидкість$v$ фотона залежатиме від його енергії і ніколи не може бути такою великою, як$c$. Оцініть відносний розмір$(c-v)/c$ розбіжності в швидкості, у випадку фотона з частотою 1 кГц, що лежить в дуже низькочастотному радіодіапазоні. \ hans {hans: фотонна маса}

41. Водень - єдиний елемент, енергетичні рівні якого можуть бути виражені точно в рівнянні. Обчисліть$\lambda_E/\lambda_F$ співвідношення довжин хвиль переходів, маркованих E і F в задачі 25 на с. 898. Висловлюйте свою відповідь як точний дріб, а не десяткове наближення. В експерименті, в якому вимірюються атомні довжини хвиль, це співвідношення забезпечує природну, сувору перевірку точності результатів. (Перевірка відповіді доступна на сайті lightandmatter.com)

42. Дайте числове порівняння кількості фотонів в секунду, випромінюваних стоватним FM-радіопередавачем і стоватної лампочкою. (Перевірка відповіді доступна на сайті lightandmatter.com)

e/Задача 43.

43. На стор. 884-885 підрозділу 13.4.4 ми використали просту алгебру для отримання наближеного виразу для енергій станів у водні, без необхідності явно розв'язувати рівняння Шредінгера. Як вхід до розрахунку ми використовували пропорційність$U \propto r^{-1}$, яка є характеристикою електричної взаємодії. Результат для енергії малюнка стоячої хвилі був$E_n \propto n^{-2}$.$n$

Є й інші системи фізичного інтересу, в яких ми маємо$U \propto r^k$ для цінностей$k$ крім того$-1$. Задача 23 обговорює основний стан гармонічного осцилятора, з$k=2$ (і позитивною константою пропорційності). У фізиці частинок системи, звані шармонієм і донтомонієм, складаються з пар субатомних частинок, званих кварками, які взаємодіють відповідно до$k=1$, тобто сили, яка не залежить від відстані. (Тут ми маємо позитивну константу пропорційності, причому$r>0$ за визначенням. Рух виявляється не надто релятивістським, тому рівняння Шредінгера є розумним наближенням.) На малюнку показані фактичні рівні енергії для цих трьох систем, намальовані з різними енергетичними шкалами, щоб всі вони могли бути показані поруч. Послідовність енергій у водні наближається до межі, яка є енергією, необхідною для іонізації атома. У шармонії відомі лише перші три рівня. ⁸

Узагальнити метод, який використовується для$k=-1$ будь-якого значення$k$, і знайти показник$j$ в отриманій пропорційності$E_n \propto n^j$. Порівняйте теоретичний розрахунок з поведінкою реальних енергій, показаних на малюнку. Прокоментуйте ліміт$k\rightarrow\infty$. (Перевірка відповіді доступна на сайті lightandmatter.com)

44. Електрон, протон і нейтрон були відкриті відповідно в 1897, 1919 і 1932 роках. Нейтрон запізнився на вечірку, і деякі фізики вважали, що не потрібно вважати його фундаментальним. Можливо, це можна пояснити як просто протон з електроном, захопленим всередині нього. Заряди скасували б, надаючи композитній частинці правильний нейтральний заряд, і маси принаймні приблизно мали сенс (нейтрон важчий за протон). (а) Враховуючи, що діаметр протона знаходиться на порядку$10^{-15}\ \text{m}$, використовуйте принцип невизначеності Гейзенберга для оцінки мінімального імпульсу захопленого електрона. (Перевірка відповіді доступна на сайті lightandmatter.com)
(b) Знайти мінімальну кінетичну енергію електрона. (Перевірка відповіді доступна на lightandmatter.com)
(c) Показати через$E=mc^2$ те, що запропоноване пояснення не вдається, оскільки внесок у масу нейтрона від кінетичної енергії електрона буде на багато порядків занадто великим.

45. Припустимо, що електрон в одному вимірі обмежений певною областю простору так, що його хвильова функція задається

$$\begin{equation*} \Psi = \begin{cases} 0 & \text{if } x\lt0 \\ A \sin(2\pi x/L) & \text{if } 0\le x\le L \\ 0 & \text{if } x>L \end{cases} \end{equation*}$$

Визначте константу$A$ від нормалізації. (Перевірка відповіді доступна на сайті lightandmatter.com)

46. У наступному,$x$ і$y$ є змінними, while$u$ і$v$ є константами. Обчислення (а)$\partial(ux\ln (vy))/\partial x$, (б)$\partial(ux\ln (vy))/\partial y$. (Перевірка відповіді доступна на сайті lightandmatter.com)

47. (а) Радіопередавач випромінює потужність$P$ у всіх напрямках, так що енергія поширюється сферично. Знайти щільність енергії на відстані$r$. (Перевірка відповіді доступна на lightandmatter.com)
(б) Нехай довжина хвилі буде$\lambda$. Як описано в прикладі 8 на стор. 842, знайти кількість фотонів в об'ємі$\lambda^3$ на цій відстані$r$. (Перевірка відповіді доступна на lightandmatter.com)
(c) Для радіопередавальної станції 1000 кГц AM, припускаючи розумні значення$P$ і$r$, перевірити, як стверджується в прикладі, що результат від частини b дуже великий.

Contributors and Attributions

Template:ContribCrowell