14.4: Атом

Ви можете багато чому навчитися, взявши двигун автомобіля один від одного, але ви дізналися набагато більше, якщо зможете знову скласти все разом і змусити його працювати. Половина роботи редукціонізму полягає в тому, щоб розбити природу на її найменші частини і зрозуміти правила, які ці частини підкоряються. Друга половина - показати, як ці частини йдуть разом, і це наша мета в цьому розділі. Ми бачили, як певні особливості всіх атомів можна пояснити на загальній основі з точки зору властивостей зв'язаних станів, але такий аргумент явно не може розповісти нам жодних деталей поведінки атома або пояснити, чому один атом діє інакше, ніж інший.

Найбільшим збентеженням для редукціоністів є те, що робота зі складання речей назад робота, як правило, набагато важче, ніж їх розбирати. Через сімдесят років після того, як були вирішені основи атомної фізики, тільки починає можливий точний розрахунок властивостей атомів, які мають багато електронів. Системи, що складаються з безлічі атомів, ще важче. Виробники суперкомп'ютерів вказують на складання великих білкових молекул як на процес, розрахунок якого ледь здійсненний за допомогою їх найшвидших машин. Мета цієї глави полягає в тому, щоб дати ніжний і візуально орієнтований посібник з деякими з більш простих результатів про атоми.

Класифікація держав

Ми зосередимо свою увагу спочатку на найпростішому атомі, водні, з одним протоном і одним електроном. Ми заздалегідь трохи знаємо, чого слід очікувати від будови цього атома. Оскільки електрон пов'язаний з протоном електричними силами, він повинен відображати сукупність дискретних енергетичних станів, кожне з яких відповідає певному малюнку стоячої хвилі. Потрібно розібратися, які бувають стани і які їх властивості.

Які властивості слід використовувати для класифікації держав? Найбільш розумним підходом є використані консервовані кількості. Енергія - це одна збережена кількість, і ми вже знаємо, що кожен стан матиме певну енергію. Виявляється, однак, що однієї енергії недостатньо. Різні моделі стоячої хвилі атома можуть мати однакову енергію.

Імпульс також є збереженою величиною, але він не особливо підходить для класифікації станів електрона в атомі водню. Причина в тому, що сила між електроном і протоном призводить до безперервного обміну імпульсом між ними. (Чому це не було проблемою і для енергії? Кінетична енергія і імпульс пов'язані між собою\(K=p^2/2m\), тому набагато масивніший протон ніколи не має дуже багато кінетичної енергії. Ми робимо наближення, припускаючи, що вся кінетична енергія знаходиться в електроні, але це досить гарне наближення.)

Кутовий імпульс допомагає при класифікації. Передача моменту моменту між протоном і електроном не відбувається, так як сила між ними є центровою силою, що не виробляє крутного моменту.

a/ Вісім довжин хвиль підходять навколо цього кола (\(\ell=8\)).

Як і енергія, кутовий імпульс квантується в квантовій фізиці. Як приклад розглянемо квантову хвилю-частинку, обмежену колом, як хвиля в круговому рові, що оточує замок. Синусоїда в такому «квантовому рові» не може мати жодної старої довжини хвилі, тому що ціле число довжин хвиль повинно відповідати по колу\(C\), рову. Чим більше це ціле число, тим коротша довжина хвилі, а коротша довжина хвилі відноситься до більшого імпульсу і кутового імпульсу. Оскільки це ціле число пов'язане з моментом, ми використовуємо\(\ell\) для нього символ:

\[\begin{equation*} \lambda = C / \ell \end{equation*}\]

Кутовий імпульс дорівнює

\[\begin{equation*} L = rp . \end{equation*}\]

Ось\(r=C/2\pi \), і\(p=h/\lambda=h\ell/C\), так

\[\begin{align*} L &= \frac{C}{2\pi}\cdot\frac{h\ell}{C} \\ &= \frac{h}{2\pi}\ell \end{align*}\]

У прикладі квантового рову кутовий імпульс квантується в одиницях\(h/2\pi \). Це робить\(h/2\pi \) досить важливе число, тому ми визначаємо абревіатуру\(\hbar=h/2\pi \). Цей символ читається «h-bar».

По суті, це цілком загальний факт в квантовій фізиці, а не просто факт про квантовий рів:

Квантування кутового моменту

Кутовий імпульс частинки, обумовлений її рухом через простір, квантується в одиницях\(\hbar\).

Вправа\(\PageIndex{1}\)

Що таке кутовий момент хвильової функції, показаної на початку розділу?

Відповідь

(відповідь у зворотному боці PDF-версії книги)

Три виміри

Наше обговорення квантово-механічного кутового моменту досі обмежувалося обертанням у площині, для чого ми можемо просто використовувати позитивні та негативні знаки для позначення напрямків обертання за годинниковою стрілкою та проти годинникової стрілки. Атом водню, однак, неминуче тривимірний. Класична обробка моменту моменту в тривимірному вимірі представлена в розділі 4.3; загалом кутовий момент частинки визначається як векторний перехресний добуток\(\mathbf{r}\times\mathbf{p}\).

Тут є основна проблема: кутовий момент електрона в атомі водню залежить як від його відстані від протона, так і\(\mathbf{r}\) від його імпульсу\(\mathbf{p}\), тому для того, щоб точно знати його кутовий момент, здавалося б, нам потрібно було б знати і його положення, і його імпульс одночасно. з хорошою точністю. Це, однак, здається, заборонено принципом невизначеності Гейзенберга.

Насправді принцип невизначеності встановлює обмеження на те, що можна знати про вектор кутового моменту частинки, але це не заважає нам знати її величину як точне ціле число, кратне\(\hbar\). Причина полягає в тому, що в трьох вимірах дійсно існують три окремі принципи невизначеності:

\[\begin{align*} \Delta p_x \Delta x &\gtrsim h \\ \Delta p_y \Delta y &\gtrsim h \\ \Delta p_z \Delta z &\gtrsim h \end{align*}\]

b/ Узгодження принципу невизначеності з визначенням кутового моменту.

Тепер розглянемо частку, b /1, яка рухається вздовж\(x\) осі в положенні\(x\) і з імпульсом\(p_x\). Можливо, ми не зможемо точно знати обидва\(x\) і\(p_x\) з необмеженою точністю, але ми все ще можемо точно знати кутовий момент частинки про походження: він дорівнює нулю, тому що частка рухається безпосередньо від походження.

Припустимо, з іншого боку, частка знаходить себе, b /2, в положенні\(x\) вздовж\(x\) осі, і вона рухається паралельно\(y\) осі з імпульсом\(p_y\). Він має кутовий момент\(xp_y\) навколо\(z\) осі, і знову ми можемо знати його кутовий момент з необмеженою точністю, тому що принцип невизначеності стосується лише\(p_x\) і\(x\)\(y\) до\(p_y\). Це не\(x\) стосується\(p_y\).

Як показано на цих прикладах, принцип невизначеності не обмежує точність наших знань про кутові моменти так сильно, як можна собі уявити. Однак це заважає нам знати всі три компоненти вектора кутового імпульсу одночасно. Найбільш загальним твердженням з цього приводу є наступна теорема, яку ми представляємо без доказів:

Вектор кутового імпульсу в квантовій фізиці

Найбільше, що можна знати про векторі моменту моменту, - це його величина і одна з трьох його векторних складових. Обидва квантуються в одиницях\(\hbar\).

c/Перетин хвильової функції водню.

Атом водню

Виведення хвильових функцій станів атома водню з перших принципів було б математично занадто складним для цієї книги, але зрозуміти логіку такої хвильової функції в візуальному плані неважко. Розглянемо хвильову функцію від початку розрізу, яка відтворюється на малюнку в. Хоча графік виглядає тривимірним, насправді це лише подання частини хвильової функції, що лежить у двовимірній площині. Третя (вгору-вниз) розмірність графіка представляє значення хвильової функції в заданій точці, а не третій вимір простору. Площина, обрана для графіка, є перпендикулярною вектору моменту моменту.

Кожне кільце піків і долин має вісім довжин хвиль, що йдуть по колу, так що цей стан має\(L=8\hbar\), тобто ми позначаємо його\(\ell=8\). Довжина хвилі коротша біля центру, і це має сенс, оскільки, коли електрон знаходиться близько до ядра, він має меншу електричну енергію, вищу кінетичну енергію та більший імпульс.

Між кожним кільцем піків в цій хвильовій функції розташовується вузлова окружність, тобто коло, на якій хвильова функція дорівнює нулю. Повна тривимірна хвильова функція має вузлові сфери: ряд вкладених сферичних поверхонь, на яких вона дорівнює нулю. Число радіусів, при яких виникають вузли, в тому числі\(r=\infty\)\(n\), називається, і\(n\) виявляється тісно пов'язаним з енергією. Основний стан має\(n=1\) (єдиний вузол тільки при\(r=\infty\)), а більш високі енергетичні стани мають більш високі\(n\) значення. Існує просте рівняння, що відноситься\(n\) до енергії, про яке ми розповімо в підрозділі 13.4.4.

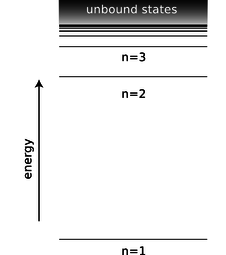
d/Енергія стану в атомі водню залежить тільки від його\(n\) квантового числа.

Числа\(n\) і\(\ell\), які ідентифікують стан, називаються його квантовими числами. Стан заданий\(n\) і\(\ell\) може орієнтуватися в самих різних напрямках в просторі. Ми могли б спробувати вказати орієнтацію за допомогою трьох квантових чисел\(\ell_x=L_x/\hbar\)\(\ell_y=L_y/\hbar\), і\(\ell_z=L_z/\hbar\). Але ми вже бачили, що неможливо знати всі три з них одночасно. Щоб дати найбільш повний можливий опис стану, ми вибираємо довільну вісь, скажімо\(z\) вісь, і позначаємо стан відповідно\(n\)\(\ell\), і\(\ell_z\). ⁶

Кутовий імпульс вимагає руху, а рух передбачає кінетичну енергію. Таким чином, неможливо мати задану кількість кутового моменту, не маючи певної кількості кінетичної енергії, а також. Так як енергія відноситься до\(n\) квантового числа, це означає, що для заданої\(n\) величини буде максимально можливий. Виходить, що це максимальне значення дорівнює\(n-1\).

Загалом, можна перерахувати можливі комбінації квантових чисел наступним чином:

п може дорівнювати 1, 2, 3,...

l може варіюватися від 0 до n − 1, з кроком 1

l z може варіюватися від усіх рушників, з кроком 1

Застосовуючи ці правила, ми маємо наступний перелік держав:

п = 1,	л = 0,	л з = 0	одна держава
п = 2,	л = 0,	л з = 0	одна держава
п = 2,	л = 1,	л з =-1, 0, або 1	три держави

самостійна перевірка:

Продовжити список для\(n=3\).

(відповідь у зворотному боці PDF-версії книги)

На малюнку е на сторінці 882 показані найнижчі енергетичні стани атома водню. У лівій колонці графіків відображаються хвильові функції в\(x-y\) площині, а правий - розподіл ймовірностей в тривимірному поданні.

e/Три стани атома водню, що мають найнижчі енергії.

Питання для обговорення

◊ Квантове число\(n\) визначається як число радіусів, при яких хвильова функція дорівнює нулю, в тому числі\(r=\infty\). Віднесіть це з особливостями фігур на лицьовій сторінці.

◊ Виходячи з визначення\(n\), чому не може бути такого поняття, як\(n=0\) держава?

◊ Зіставте особливості графіків хвильових функцій на малюнку е з відповідними особливостями картинок розподілу ймовірностей.

◊ Як ви можете визначити з графіків хвильових функцій на малюнку е, які з них мають які кутові моменти?

◊ Критикуйте наступне неправильне твердження: «\(\ell=8\)Хвильова функція на малюнку c має коротшу довжину хвилі в центрі, оскільки в центрі електрон знаходиться на більш високому енергетичному рівні».

◊ Обговорюємо наслідки того факту, що хмара ймовірності в тому\(n=2\),\(\ell=1\) стан розбивається на дві частини.

Енергії станів у водні

Історія

Експериментальною методикою точного вимірювання енергетичних рівнів атома є спектроскопія: дослідження спектра випромінюваного (або поглиненого) атомом світла. Тільки фотони з певними енергіями можуть випромінюватися або поглинатися атомом водню, наприклад, оскільки кількість енергії, отриманої або втраченої атомом, має дорівнювати різниці в енергії між початковим і кінцевим станами атома. Спектроскопія стала високорозвиненим мистецтвом за кілька десятиліть до того, як Ейнштейн навіть запропонував фотон, і швейцарський спектроскопіст Йоганн Бальмер визначив у 1885 році, що існує просте рівняння, яке дає всі довжини хвиль, що випромінюються воднем. У сучасних умовах ми розглядаємо довжини хвиль фотонів лише як непрямі докази базових енергетичних рівнів атома, і ми переробляємо результат Балмера в рівняння для цих рівнів атомної енергії:

\[\begin{equation*} E_n = -\frac{2.2\times10^{-18}\ \text{J}}{n^2} , \end{equation*}\]

Ця енергія включає в себе як кінетичну енергію електрона, так і електричну енергію. Нульовий рівень шкали електричної енергії обраний як енергія електрона і протона, які знаходяться нескінченно далеко один від одного. При такому виборі негативні енергії відповідають зв'язаним станам, а позитивні - незв'язаним.

Звідки\(2.2\times10^{-18}\ \text{J}\) береться таємничий числовий коефіцієнт? У 1913 році датський теоретик Нільс Бор зрозумів, що вона точно чисельно дорівнює певній комбінації фундаментальних фізичних констант:

\[\begin{equation*} E_n = -\frac{mk^2e^4}{2\hbar^2}\cdot\frac{1}{n^2} , \end{equation*}\]

де\(m\) - маса електрона, і\(k\) - постійна сили Кулона для електричних сил.

Бор зміг приготувати висновок цього рівняння на основі неповної версії квантової фізики, яка була розроблена на той час, але його виведення сьогодні в основному представляє історичний інтерес. Він передбачає, що електрон йде круговим шляхом, тоді як все поняття шляху для частинки вважається безглуздим в нашому більш повному сучасному варіанті квантової фізики. Хоча Бор зміг створити правильне рівняння для енергетичних рівнів, його модель також дала різні неправильні результати, такі як прогнозування того, що атом буде плоским, і що стан землі матиме\(\ell=1\) скоріше, ніж правильний\(\ell=0\).

приблизне лікування

Замість того, щоб стрибати прямо в повне математичне лікування, ми почнемо з пошуку деякого фізичного розуміння, що призведе до приблизного аргументу, який правильно відтворює форму рівняння Бора.

Типова картина стоячої хвилі для електрона складається з центральної коливальної області, оточеної областю, в якій хвильова функція відступає. Як обговорювалося в підрозділі 13.3.6, коливальний тип малюнка зазвичай зустрічається в класично дозволеній області, тоді як відходження відбувається в класично забороненій області, де електрон має недостатню кінетичну енергію для проникнення відповідно до класичної фізики. Використовується символ\(r\) радіуса сферичної межі між класично дозволеними та класично забороненими регіонами. Класично\(r\) було б відстань від протона, на якому електрон повинен був би зупинитися, розвернутися і повернутися назад.

\(r\)Якби мали однакове значення для кожної стоячої хвилі, то ми б по суті вирішували проблему частинки в коробці в трьох вимірах, причому коробка є сферичною порожниною. Розглянемо енергетичні рівні частинки в коробці порівняно з рівнями атома водню, f.

f/Енергетичні рівні частинки в коробці, на відміну від рівнів атома водню.

Вони якісно різні. Енергетичні рівні частинки в коробці стають все далі і далі один від одного, коли ми йдемо вище в енергії, і ця особливість навіть не залежить від деталей того, чи є коробка двовимірною чи тривимірною, або її точної форми. Причина розкидання полягає в тому, що коробка приймається абсолютно непроникною, тому її розмір\(r\), фіксований. Хвильовий малюнок з\(n\) горбами має довжину хвилі, пропорційну\(r/n\), а отже, імпульс пропорційний\(n\), і енергію, пропорційну\(n^2\). Однак у атомі водню сила, що утримує електронний зв'язок, не є нескінченною силою, що зустрічається, коли вона відскакує від стіни, це приваблива електрична сила від ядра. Якщо ми вкладаємо більше енергії в електрон, це як кинути кульку вгору з вищою енергією - він вийде далі, перш ніж повертатися вниз. Це означає, що в атомі водню ми\(r\) очікуємо збільшення, коли ми переходимо до станів вищої енергії. Це, як правило, утримує довжини хвиль високоенергетичних станів від занадто коротких, зменшуючи їх кінетичну енергію. Ближче і тісніше скупчення енергетичних рівнів у водні також має сенс, оскільки ми знаємо, що існує певна енергія, якої було б достатньо, щоб електрон повністю втечу, і тому послідовність зв'язаних станів не може поширюватися вище цієї енергії.

Коли електрон знаходиться на максимально класично дозволеній відстані\(r\) від протона, він має нульову кінетичну енергію. Таким чином, коли електрон знаходиться на відстані\(r\), його енергія чисто електрична:

\[\begin{equation*} E = -\frac{ke^2}{r} \tag{1} \end{equation*}\]

Тепер настає наближення. Насправді довжина хвилі електрона не може бути постійною в класично дозволеній області, але ми робимо вигляд, що це так. \(n\)Оскільки кількість вузлів у хвильовій функції, ми можемо інтерпретувати її приблизно як кількість довжин хвиль, які підходять по діаметру\(2r\). Ми навіть не намагаємося зробити деривацію, яка б виробляла всі правильні числові фактори, такі як 2\(\pi \) і так далі, тому ми просто робимо наближення

\[\begin{equation*} \lambda \sim \frac{r}{n} . \tag{2} \end{equation*}\]

Нарешті припустимо, що типова кінетична енергія електрона знаходиться на тому ж порядку, що і абсолютна величина його сумарної енергії. (Це вірно в межах двох разів для типової класичної системи, як планета на круговій орбіті навколо Сонця.) У нас тоді є

\[\begin{align*} \text{absolute}&\text{ value of total energy} \\ &= \frac{ke^2}{r} \notag \\ &\sim K \notag = p^2/2m \notag \\ &= (h/\lambda)^2/2m \notag \\ &\sim h^2n^2/2mr^2 \tag{3} \end{align*}\]

Тепер ми вирішуємо рівняння\(ke^2/r \sim h^2n^2 / 2mr^2\) для\(r\) і викидаємо числові коефіцієнти, які ми не можемо сподіватися, що отримали право, поступаючись

\[\begin{equation*} r \sim \frac{h^2n^2}{mke^2} .\tag{4} \end{equation*}\]

\(n=1\)Підключення до цього рівняння дає\(r=2\) нм, який дійсно знаходиться на потрібному порядку. Нарешті, ми об'єднаємо рівняння (4) і (1), щоб знайти

\[\begin{equation*} E \sim -\frac{mk^2e^4}{h^2n^2} , \end{equation*}\]

що є правильним, за винятком числових факторів, які ми ніколи не прагнули знайти.

Точна обробка стану грунту

Загальний доказ рівняння Бора для всіх значень\(n\) виходить за рамки математичної сфери цієї книги, але перевірити його для конкретної досить просто\(n\), особливо з огляду на щасливе припущення про те, яку функціональну форму спробувати для хвильової функції. Форма, яка працює для наземного стану, є

\[\begin{equation*} \Psi = ue^{-r/a} , \end{equation*}\]

\(r=\sqrt{x^2+y^2+z^2}\)де відстань електрона від протона, і\(u\) передбачає нормалізацію. У наступному результат\(\partial r/\partial x=x/r\) стане в нагоді. Обчисливши часткові похідні, що зустрічаються у лапласа, отримаємо за\(x\) термін

\[\begin{align*} \frac{\partial\Psi}{\partial x} &= \frac{\partial \Psi}{\partial r} \frac{\partial r}{\partial x} \\ &= -\frac{x}{ar} \Psi \\ \frac{\partial^2\Psi}{\partial x^2} &= -\frac{1}{ar} \Psi -\frac{x}{a}\left(\frac{\partial}{dx}\frac{1}{r}\right)\Psi+ \left( \frac{x}{ar}\right)^2 \Psi\\ &= -\frac{1}{ar} \Psi +\frac{x^2}{ar^3}\Psi+ \left( \frac{x}{ar}\right)^2 \Psi , \text{so} \nabla^2\Psi &= \left( -\frac{2}{ar} + \frac{1}{a^2} \right) \Psi . \end{align*}\]

Рівняння Шредінгера дає

\[\begin{align*} E\cdot\Psi &= -\frac{\hbar^2}{2m}\nabla^2\Psi + U\cdot\Psi \\ &= \frac{\hbar^2}{2m}\left( \frac{2}{ar} - \frac{1}{a^2} \right)\Psi -\frac{ke^2}{r}\cdot\Psi \end{align*}\]

Якщо ми вимагаємо, щоб це рівняння трималося для всіх\(r\), то ми повинні мати рівність як для членів форми, так\((\text{constant})\times\Psi\) і для тих, що мають форму\((\text{constant}/r)\times\Psi\). Це означає

\[\begin{align*} E &= -\frac{\hbar^2}{2ma^2} \\ \text{and} \\ 0 &= \frac{\hbar^2}{mar} -\frac{ke^2}{r} . \end{align*}\]

Ці два рівняння можна вирішити для невідомих\(a\) і\(E\), даючи

\[\begin{align*} a &= \frac{\hbar^2}{mke^2} \\ \text{and}\\ E &= -\frac{mk^2e^4}{2\hbar^2} , \end{align*}\]

де результат для енергії узгоджується з рівнянням Бора для\(n=1\). Розрахунок константи нормалізації\(u\) відводиться до домашньої задачі 36.

Вправа\(\PageIndex{1}\)

Ми перевірили, що функція\(\Psi = he^{-r/a}\) є розв'язком рівняння Шредінгера, і все ж вона має злам в ньому\(r=0\). Що тут відбувається? Хіба я раніше не сперечався, що перегини нефізичні?

Відповідь

(відповідь у зворотному боці PDF-версії книги)

Приклад\(\PageIndex{1}\): Wave phases in the hydrogen molecule

У прикладі 16 на сторінці 861 я стверджував, що існування\(\text{H}_2\) молекули можна по суті пояснити аргументом частинки в коробці: молекула є більшою коробкою, ніж окремий атом, тому довжина хвилі кожного електрона може бути довшою, її кінетична енергія нижча. Тепер, коли ми маємо математичний вираз для хвильової функції атома водню в його основному стані, ми можемо зробити цей аргумент трохи більш суворим і детальним. Припустимо, що два атома водню знаходяться у відносно прохолодному зразку одноатомного водневого газу. Оскільки газ прохолодний, ми можемо припустити, що атоми знаходяться в їх наземних станах. Тепер припустимо, що два атоми наближаються один до одного. Використовуючи знову припущення, що газ прохолодний, розумно уявити, що атоми наближаються один до одного повільно. Тепер атоми підійшли трохи ближче, але все ще досить далеко один від одного, що область між ними класично заборонена. Кожен електрон може тунелювати через цю класично заборонену область, але ймовірність тунелювання невелика. Кожен з них зараз зустрічається з, скажімо, 99% ймовірністю в своєму первісному будинку, але з 1% ймовірністю в іншому ядрі. Кожен електрон зараз знаходиться в стані, що складається з суперпозиції основного стану власного атома з наземним станом іншого атома. У накладеній хвильовій функції є два піки, але один є набагато більшим піком, ніж інший.

Зараз виникає цікаве питання. Які відносні фази двох електронів? Як обговорюється на сторінці 855, абсолютна фаза хвильової функції електрона насправді не є значущим поняттям. Припустимо, атом А містить електрон Аліса, і B електрон Боб. Незадовго до зіткнення Аліса, можливо, задумалася: «Чи є моя фаза позитивна зараз, чи вона негативна? Але, звичайно, я не повинна ставити собі такі дурні питання», - вівчаво додає вона.

g/ Приклад 23.

Але відносні фази чітко визначені. Коли два атоми наближаються все ближче і ближче один до одного, ймовірність тунелювання зростає і в кінцевому підсумку стає настільки високою, що кожен електрон витрачає по суті 50% свого часу в кожному атомі. Зараз розумно уявити, що будь-яка з двох можливостей може отримати. Хвильова функція Аліси може виглядати як g /1, з двома піками у фазі один з одним, або це може виглядати як g /2, з протилежними фазами. Оскільки відносні фази хвильових функцій чітко визначені, стани 1 і 2 фізично помітні. Зокрема, кінетична енергія стану 2 набагато вища; грубо кажучи, це як двогорбистий хвильовий малюнок частинки в коробці, на відміну від 1, який виглядає приблизно як одногорбистий візерунок з набагато більшою довжиною хвилі. Мало того, але електрон у стані 1 має велику ймовірність знайти в центральній області, де він має велику негативну електричну енергію завдяки взаємодії з обома протонами. Держава 2, з іншого боку, має низьку ймовірність існування в цьому регіоні. Таким чином, стан 1 представляє справжню хвильову функцію\(\text{H}_2\) молекули, і введення Аліси і Боба в цей стан призводить до меншої енергії, ніж їх загальна енергія при розділенні, тому молекула пов'язана, і не розлетиться спонтанно.

Стан g /3, з іншого боку, фізично не відрізняється від g /2, а також g /4 від g /1. Аліса може сказати Бобу: «Хіба це не чудово, що ми перебуваємо в стані 1 або 4? Я люблю бути стабільним, як це». Але вона знає, що не має сенсу запитати себе в даний момент, в якому стані вона знаходиться, 1 або 4.

Рішення

Додайте сюди текст.

Питання для обговорення

• Стани водню з\(n\) більшим, ніж близько 10, ніколи не спостерігаються на сонці. Чому це може бути?
• Намалюйте графіки\(r\) та\(E\) проти\(n\) водню та порівняйте з аналогічними графіками для одновимірної частинки в коробці.

Електронний спін

Це бентежить початківця пінг-понгу, щоб вперше зіткнутися з більш кваліфікованим гравцем, який може покласти спина на м'яч. Незважаючи на те, що ви не можете бачити, що м'яч обертається, ви можете сказати, що щось відбувається тим, як він взаємодіє з іншими об'єктами у своєму оточенні. Таким же чином ми можемо сказати з того, як електрони взаємодіють з іншими речами, що вони мають власний власний спін. Експерименти показують, що навіть коли електрон не рухається через простір, він все ще має кутовий імпульс, що дорівнює\(\hbar/2\).

h/Вершина має кутовий імпульс як через рух свого центру маси через простір, так і за рахунок внутрішнього обертання. Електронний спін приблизно аналогічний внутрішньому спину вершини.

Це може здатися парадоксальним, оскільки квантовий рів, наприклад, давав лише кутові моменти, які були цілими кратними\(\hbar\), а не напіводиницям, і я стверджував, що кутовий імпульс завжди квантувався в одиницях\(\hbar\), а не лише у випадку квантового рів. Однак вся ця дискусія передбачала, що кутовий імпульс буде надходити від руху частинки через простір. \(\hbar/2\)Кутовий імпульс електрона - це просто властивість частинки, як її заряд або її маса. Він не має нічого спільного з тим, рухається електрон чи ні, і він не виходить від будь-якого внутрішнього руху всередині електрона. Нікому ніколи не вдавалося знайти жодної внутрішньої структури всередині електрона, і навіть якби там була внутрішня структура, математично неможливо було б її привести в піводиниці кутового моменту.

Ми просто повинні прийняти цей момент моменту\(\hbar/2\), який називається «спином» електрона - матінка-природа втирає в нього ніс як спостережуваний факт.

Протони і нейтрони мають однаковий\(\hbar/2\) спін, тоді як фотони мають внутрішній спін\(\hbar\). Взагалі, напівцілочисельні спини характерні для матеріальних частинок. Знайдено інтегральні значення для частинок, що несуть сили: фотони, які втілюють електричне і магнітне поля сили, а також більш екзотичних посланників ядерних і гравітаційних сил.

Як і у випадку зі звичайним моментом, ми можемо описати спіновий кутовий імпульс з точки зору його величини та його складової вздовж заданої осі. Пишемо\(s\) і\(s_z\) для цих величин, виражених в одиницях\(\hbar\), тому електрон має\(s=1/2\) і\(s_z=+1/2\) або\(-1/2\).

Враховуючи спін електронів, нам потрібно загалом чотири квантові числа, щоб позначити стан електрона в атомі водню:\(n\),\(\ell\),\(\ell_z\), і\(s_z\). (Ми опускаємо,\(s\) тому що він завжди має однакове значення.) Символи і включають лише кутовий імпульс електрон, оскільки він рухається через простір, а не його спіновий кутовий імпульс. Наявність двох можливих спінових станів електрона призводить до подвоєння чисел станів:

п = 1,	л = 0,	л з = 0,	s z = + 1/2 або − 1/2	дві держави
п = 2,	л = 0,	л з = 0,	s z = + 1/2 або − 1/2	дві держави
п = 2,	л = 1,	л з =-1, 0, або 1	s z = + 1/2 або − 1/2	шість штатів

Примітка про позначення

На жаль, існує дві непослідовні системи позначень квантових чисел, про які ми говорили. Позначення, яке я використовував, - це те, що використовується в ядерній фізиці, але є інше, яке використовується в атомній фізиці.

ядерна фізика	атомна фізика
п	той же
л	той же
л х	без позначення
л у	без позначення
л з	м
s = 1/2	без позначення (іноді σ)
х х	без позначення
S у	без позначення
s z	s

Позначення ядерної фізики є більш логічним (не надаючи особливого статусу\(z\) осі) і більш запам'ятовується (\(\ell_z\)а не незрозумілим\(m\)), тому я використовую його послідовно в цій книзі, хоча майже всі програми, які ми розглянемо, є атомними.

Ми також обтяжені наступними історично похідними літерними етикетками, які заслуговують на усунення на користь більш простих числових:

l=0	l=1	л = 2	l=3
s	р	d	f

п = 1	п = 2	п = 3	п = 4	п = 5	п = 6	п = 7
К	Л	М	П	O	Р	Q

Мітки spdf використовуються як в ядерній ⁷, так і в атомній фізиці, тоді як літери KLMNOPQ використовуються лише для позначення станів електронів.

І нарешті, є шматок позначення, який є хорошим і корисним, але про який я просто ще не згадував. Вектор\(\mathbf{j}=\v c{\ell}+\mathbf{s}\) позначає сумарний момент моменту частинки в одиницях\(\hbar\), включаючи як орбітальну, так і спінову частини. Це квантове число виявляється дуже корисним в ядерній фізиці, оскільки ядерні сили мають тенденцію обмінюватися орбітальним і спіновим кутовим імпульсом, тому даний енергетичний рівень часто містить суміш\(\ell\) і\(s\) значення, залишаючись при цьому досить чистими з точки зору\(j\).

13.4.6 Атоми з більш ніж одним електроном

А як щодо інших атомів, крім водню? Здавалося б, все стало б набагато складніше з додаванням другого електрона. Атом водню має лише одну частинку, яка багато рухається навколо, оскільки ядро настільки важке і майже нерухоме. Гелій, з двома, був би безладом. Замість хвильової функції, квадрат якої говорить нам про ймовірність знаходження одного електрона в будь-якому заданому місці в просторі, атом гелію повинен мати хвильову функцію, квадрат якої вказував би нам ймовірність знаходження двох електронів у будь-якій заданій комбінації точок. Ой! Крім того, ми мали б додаткове ускладнення електричної взаємодії між двома електронами, а не в змозі уявити все з точки зору електрона, що рухається в статичному силовому полі, створеному лише ядром.

Незважаючи на все це, виявляється, що ми можемо отримати напрочуд хороший опис багатоелектронних атомів, просто припускаючи, що електрони можуть займати ті самі шаблони стоячої хвилі, які існують в атомі водню. Наприклад, основний стан гелію мав би обидва електрони в станах, які дуже схожі на\(n=1\) стани водню. Другий найнижчий енергетичний стан гелію мав би один електрон у\(n=1\) стані, а інший - у\(n=2\) станах. Щодо складні спектри елементів, важчих за водню, можна розуміти як виникають внаслідок великої кількості можливих комбінацій станів для електронів.

Дивна річ трапляється, однак, з літієм, триелектронним атомом. Ми очікуємо, що основний стан цього атома буде таким, в якому всі три електрони осідають у\(n=1\) стани. Що насправді відбувається, так це те, що два електрони переходять у\(n=1\) стани, але третій залишається в\(n=2\) стані. Це наслідок нового принципу фізики:

Принцип виключення Паулі

Тільки один електрон може коли-небудь займати даний стан.

Є два\(n=1\) стани, один з\(s_z=+1/2\) і один з\(s_z=-1/2\), але немає третього\(n=1\) стану для займання третього електрона літію, тому він змушений переходити в\(n=2\) стан.

Математично можна довести, що принцип виключення Паулі застосовується до будь-якого типу частинок, що має напівціле спін. Таким чином, два нейтрони ніколи не можуть займати один і той же стан, а також для двох протонів. Фотони, однак, несприйнятливі до принципу виключення, оскільки їх спін є цілим числом.

Виведення таблиці Менделєєва

i/Початок таблиці Менделєєва.

Тепер можна врахувати структуру таблиці Менделєєва, яка здалася такою загадковою навіть її винахіднику Менделєєву. Перший ряд складається з атомів з електронами тільки в\(n=1\) станах:

Ч	1 електрон в n = 1 стані
Він	2 електрони в двох n = 1 станах

Наступний ряд будується шляхом заповнення\(n=2\) енергетичними рівнями:

Лі	2 електрона в n = 1 станах, 1 електрон в n = 2 стані
Бути	2 електрони в n = 1 станах, 2 електрони в n = 2 станах
...
O	2 електрони в n = 1 станах, 6 електронів в n = 2 станах
F	2 електрони в n = 1 станах, 7 електронів в n = 2 станах
Ne	2 електрони в n = 1 станах, 8 електронів в n = 2 станах

У третьому ряду починаємо на\(n=3\) рівні:

Na	2 електрона в n = 1 станах, 8 електронів в n = 2 станах, 1 електрон в n = 3 стані

Тепер ми можемо побачити логічний зв'язок між наповненням енергетичних рівнів і структурою таблиці Менделєєва. Стовпець 0, наприклад, складається з атомів з потрібною кількістю електронів для заповнення всіх наявних станів аж до певного значення\(n\). Колонка I містить атоми, такі як літій, які мають лише на один електрон більше, ніж це.

Це показує, що стовпці стосуються заповнення енергетичних рівнів, але чому це має щось спільне з хімією? Чому, наприклад, елементи в колонках I і VII небезпечно реагують?

j/Водень має високу реакцію.

Розглянемо, наприклад, елемент натрій (Na), який настільки реактивний, що при впливі повітря може спалахнути полум'ям. Електрон в\(n=3\) стані володіє надзвичайно високою енергією. Якщо ми дозволимо атому натрію контактувати з атомом кисню, енергія може бути вивільнена шляхом перенесення\(n=3\) електрона з натрію в одне з вакантних\(n=2\) станів нижчої енергії в кисні. Ця енергія трансформується в тепло. Будь-який атом в колонці I високореактивний з тієї ж причини: він може вивільняти енергію, віддаючи електрон, який має надзвичайно високу енергію.

Колонка VII ефектно реактивна з протилежної причини: ці атоми мають єдину вакансію в низькоенергетичному стані, тому енергія виділяється, коли ці атоми крадуть електрон у іншого атома.

Може здатися, що ці аргументи пояснюють лише реакції атомів, які знаходяться в різних рядках таблиці Менделєєва, оскільки тільки в цих реакціях перенесений електрон може переходити з вищого\(n\) стану в нижчий\(n\) стан. Це невірно. Наприклад,\(n=2\) електрон у фторі (F) мав би іншу енергію, ніж\(n=2\) електрон у літії (Li), через різну кількість протонів та електронів, з якими він взаємодіє. Грубо кажучи,\(n=2\) електрон у фторі більш щільно пов'язаний (нижче за енергією) через більшу кількість протонів, що притягують його. Ефекту збільшеної кількості притягуючих протонів лише частково протидіє збільшенням кількості відштовхуючих електронів, оскільки сили, що діють на електрон іншими електронами, знаходяться в багатьох різних напрямках і частково скасовуються.

Автори та атрибуція

Template:ContribCrowell