14.1: Правила випадковості

• З огляду на одну мить інтелект, який міг би осягнути всі сили, за допомогою яких природа оживляється, і відповідні позиції речей, які її складають... нічого не було б невизначеним, і майбутнє, як минуле, буде викладено перед його очима. - П'єр Симон де Лаплас, 1776
• Енергія, що виробляється атомом, - дуже бідна річ. Той, хто очікує джерела енергії від перетворення цих атомів, говорить самогон. - Ернест Резерфорд, 1933
• Квантова механіка дуже імпозантна. Але внутрішній голос говорить мені, що це все ще не остаточна правда. Теорія багато поступається, але навряд чи наближає нас до таємниці Старого. У будь-якому випадку, я переконаний, що Він не грає в кістки. - Альберт Ейнштейн

Як би радикальна годинникова всесвіт Ньютона здавалася його сучасникам, до початку ХХ століття вона стала свого роду незаконно прийнятою догмою. На щастя для нас, ця детермінована картина Всесвіту руйнується на атомному рівні. Найяскравіша демонстрація того, що закони фізики містять елементи випадковості, полягає в поведінці радіоактивних атомів. Виберіть два однакових атома радіоактивного ізотопу, скажімо, природного урану 238, і уважно спостерігайте за ними. Вони будуть руйнуватися в різний час, хоча різниці в їх початковій поведінці не було.

У нас були б великі неприємності, якби поведінка цих атомів була такою ж передбачуваною, як очікувалося в ньютонівському світогляді, оскільки радіоактивність є важливим джерелом тепла для нашої планети. Насправді кожен атом вибирає випадковий момент, в який вивільняється його енергія, що призводить до приємного стійкого нагрівального ефекту. Земля була б набагато холоднішою планетою, якби її нагрівали лише сонячне світло, а не радіоактивність. Напевно, не було б вулканів, а океани ніколи б не були рідкими. Глибоководні геотермальні отвори, в яких життя вперше розвивалося, ніколи б не існувало. Але був би ще гірший наслідок, якби радіоактивність була детермінованою: після декількох мільярдів років миру всі 238 атоми урану на нашій планеті, імовірно, виберуть той самий момент для розпаду. Величезна кількість накопиченої ядерної енергії, замість того, щоб бути розкинутою по еонам, все буде випущено в одну мить, підірвавши всю нашу планету до Kingdom Come. ¹

Ілюстрація\(\PageIndex{1}\): У 1980 році континентальні США отримали свій перший смак активного вулканізму в недавній пам'яті з виверженням гори Сент-Хеленс.

Нова версія фізики, що включає певні види випадковості, називається квантовою фізикою (з причин, які стануть зрозумілі пізніше). Вона представляла собою такий драматичний розрив з попередньою, детермінованою традицією, що все, що прийшло раніше, вважається «класичним», навіть теорією відносності. Цей розділ є базовим вступом до квантової фізики.

Вправа\(\PageIndex{1}\)

Я сказав: «Виберіть два однакових атома радіоактивного ізотопу». Чи справді два атоми однакові? Якщо їх електрони обертаються навколо ядра, чи можемо ми розрізнити кожен атом за певним розташуванням його електронів в якийсь момент часу?

Відповідь

Додайте сюди тексти. Не видаляйте цей текст спочатку.

13.1.1 Випадковість не є випадковою

Неприємність Ейнштейна до випадковості та його асоціація детермінізму з божественністю сходить до концепції Просвітництва Всесвіту як гігантського шматочка годинникового механізму, який тільки повинен був бути введений в рух спочатку Будівельник. Багатьох засновників квантової механіки цікавили можливі зв'язки між фізикою і східною і західною релігійно-філософською думкою, але кожна освічена людина має різне поняття релігії та філософії. Бертран Рассел зауважив: «Сер Артур Еддінгтон виводить релігію з того, що атоми не підкоряються законам математики. Сер Джеймс Джинс виводить це з того, що вони роблять».

Дотепність Рассела, яка неправильно передбачає, що математика не може описати випадковість, нагадує нам, як важливо не спростити це питання випадковості. Ви не повинні просто припускати: «Ну, це все випадково, все може статися». З одного боку, певні речі просто не можуть статися, ні в класичній фізиці, ні в квантовій фізиці. Закони збереження маси, енергії, імпульсу та моменту моменту все ще діють, тому, наприклад, процеси, які створюють енергію з нічого, не просто малоймовірні відповідно до квантової фізики, вони неможливі.

Корисну аналогію можна провести з роллю випадковості в еволюції. Дарвін не був першим біологом, який припустив, що види змінювалися протягом тривалих періодів часу. Дві його нові фундаментальні ідеї полягали в тому, що (1) зміни виникли через випадкові генетичні варіації, і (2) зміни, що підвищують здатність організму виживати та відтворюватися, будуть збережені, тоді як дезадаптивні зміни будуть усунені природним відбором. Сумнівники еволюції часто розглядають лише перший пункт, про випадковість природної варіації, але не другий пункт, про систематичну дію природного відбору. Вони роблять такі заяви, як: «розвиток складного організму, такого як Homo sapiens, через випадковий шанс було б схожим на вихор, що дме через звалище і спонтанно збирає джамбо-струмінь з металобрухту». Недолік цього типу міркувань полягає в тому, що він ігнорує детерміновані обмеження на результати випадкових процесів. Бо атом порушити збереження енергії не більш імовірно, ніж завоювання світу шимпанзе в наступному році.

Вправа\(\PageIndex{1}\)

Економісти часто поводяться як небажані фізики, ймовірно, тому, що здається престижним робити числові розрахунки замість того, щоб говорити про людські стосунки та організації, як інші соціологи. Їх прагнення змусити економіку працювати як ньютонівська фізика поширюється на паралельне використання механічних метафор, як у концепції попиту та пропозиції на ринку, що діє як саморегулююча машина, і ідеалізації людей як економічних автоматів, які послідовно прагнуть максимізувати власне багатство. Які докази є випадковість, а не механічний детермінізм в економіці?

Відповідь

Обговорення Питання - відповіді не дано.

13.1.2 Обчислення випадковості

Ви також повинні розуміти, що навіть якщо щось випадкове, ми все одно можемо це зрозуміти, і ми все одно можемо обчислювати ймовірності чисельно. Іншими словами, фізики - хороші букмекери. Хороший букмекер може розрахувати шанси на те, що кінь виграє гонку набагато точніше, ніж недосвідчена, але тим не менше не може передбачити, що буде в якійсь конкретній гонці.

Як ілюстрація загальної техніки розрахунку коефіцієнтів, припустимо, ви граєте 25-центовий ігровий автомат. Кожне з трьох коліс має один шанс на десять придумати вишеньку. Якщо всі три колеса придумати вишні, ви виграєте $100. Незважаючи на те, що результати будь-якого конкретного випробування є випадковими, ви можете зробити певні кількісні прогнози. По-перше, ви можете підрахувати, що ваші шанси на виграш на будь-якому розгляді є\(1/10\times1/10\times1/10=1/1000=0.001\). Тут я представляю ймовірності як числа від 0 до 1, що зрозуміліше, ніж твердження на кшталт «Коефіцієнти 999 до 1», і полегшує обчислення. Імовірність 0 представляє щось неможливе, а ймовірність 1 представляє те, що обов'язково станеться.

Крім того, ви можете сказати, що будь-який даний судовий процес однаково ймовірно призведе до перемоги, і не має значення, виграли ви або програли в попередніх іграх. Математично ми говоримо, що кожне випробування є статистично незалежним, або що окремі ігри не співвідносяться. Більшість гравців помилково переконані, що, навпаки, азартні ігри співвідносяться. Якщо вони грали в ігровий автомат цілий день, вони переконані, що це «готується платити», і вони не хочуть, щоб хтось інший грав машину і «використовував» джекпот, який вони «прийшли». Іншими словами, вони стверджують, що серія випробувань на ігровому автоматі негативно корелює, що програш тепер робить вас більш імовірно, щоб виграти пізніше. Гравці в Craps стверджують, що ви повинні піти до столу, де людина, яка котить кістки, «гаряча», тому що вона, швидше за все, буде продовжувати рухатися хороші цифри. Тоді гравці Craps вважають, що рулони кубиків позитивно корелюють, що виграш тепер робить вас більше шансів виграти пізніше.

Моя методика розрахунку ймовірності виграшу на ігровому автоматі стала прикладом наступного важливого правила для розрахунків, заснованих на незалежних ймовірностях:

Закон незалежних ймовірностей

Якщо ймовірність того, що одна подія трапиться є\(P_A\), а ймовірність другого статистично незалежного події є\(P_B\), то ймовірність того, що вони обидва будуть відбуватися, є добутком ймовірностей,\(P_AP_B\). Якщо задіяно більше двох подій, ви просто продовжуєте множити.

Це можна сприймати як визначення статистичної незалежності.

Зверніть увагу, що це стосується лише незалежних ймовірностей. Наприклад, якщо у вас в кишені є нікель і копійка, і ви випадковим чином витягнете один з них, є ймовірність 0,5, що це буде нікель. Якщо потім замінити монету і знову витягнути одну випадковим чином, знову є ймовірність 0,5 придумати нікель, тому що ймовірності незалежні. Таким чином, існує ймовірність 0,25, що ви отримаєте нікель обидва рази.

Припустимо замість цього, що ви не замінюєте першу монету, перш ніж витягнути другу. Тоді ви зобов'язані витягнути іншу монету вдруге, і немає ніякого способу ви могли витягнути нікель двічі. У цій ситуації два судові процеси не є самостійними, оскільки результат першого судового розгляду впливає на другий судовий розгляд. Закон незалежних ймовірностей не застосовується, а ймовірність отримання нікелю двічі дорівнює нулю, а не 0,25.

Експерименти показали, що в разі радіоактивного розпаду ймовірність того, що будь-яке ядро розпадеться протягом заданого часового інтервалу, не впливає на те, що відбувається з іншими ядрами, а також не пов'язана з тим, як довго воно пройшло без розпаду. Перше спостереження має сенс, оскільки ядра ізольовані один від одного в центрах відповідних атомів, а тому не мають фізичного способу впливу один на одного. Другий факт також розумний, так як всі атоми ідентичні. Припустимо, ми хотіли вірити, що певні атоми були «надзвичайно жорсткими», про що свідчить їхня історія незвично довгого часу без розпаду. Ці атоми повинні були б відрізнятися певним фізичним чином, але ніхто ніколи не досяг успіху в виявленні відмінностей між атомами. Немає ніякого способу змінити атом досвідом, який він має протягом свого життя.

Закон незалежних ймовірностей говорить нам використовувати множення для обчислення ймовірності того, що станеться і A, і B, припускаючи, що ймовірності незалежні. Як щодо ймовірності «або», а не «і»? Якщо дві події А і\(B\) є взаємовиключними, то ймовірність того чи іншого відбувається є сумою\(P_A+P_B\). Наприклад, казанок може мати 30% шанс отримати страйк (збивши всі десять шпильок) і 20% шанс збити дев'ять з них. Шанс казанка збивати дев'ять шпильок або десять штифтів, отже, становить 50%.

Не має сенсу додавати ймовірності речей, які не є взаємовиключними, тобто, що могло статися і те, і інше. Скажімо, у мене є 90% шансів з'їсти обід у будь-який день, і 90% шанс з'їсти вечерю. Імовірність того, що я з'їму або обід, або вечерю, не становить 180%.

Нормалізація

Якщо я обертаю глобус і випадковим чином вибираю точку на ньому, у мене є близько 70% шансів вибрати точку, яка знаходиться в океані, і 30% шанс вибрати точку на суші. Імовірність збирання або води, або землі є\(70%+30%=100%\). Вода і земля взаємовиключні, а інших можливостей немає, тому ймовірності довелося скласти до 100%. Він працює так само, якщо є більше двох можливостей - якщо ви можете класифікувати всі можливі результати в список взаємовиключних результатів, то всі ймовірності повинні скласти до 1, або 100%. Це властивість ймовірностей відомо як нормалізація.

Малюнок\(\PageIndex{2}\): Нормалізація: ймовірність пікіровки землі плюс ймовірність збору води додає до 1.

Середні

Інший спосіб боротьби з випадковістю - приймати середні показники. Казино знає, що в довгостроковій перспективі кількість разів, які ви виграєте, приблизно дорівнює кількості разів, коли ви граєте, помножене на ймовірність виграшу. У ігровому автоматі, описаній на сторінці 823, де ймовірність виграшу становить 0,001, якщо ви витратите тиждень, граючи, і заплатите $2500, щоб грати 10000 разів, ви, швидше за все, виграєте близько 10 разів\((10,000\times0.001=10)\), і зберете $1000. В середньому казино буде отримувати від вас прибуток в розмірі $1500. Це приклад наступного правила.

Правило для обчислення середніх

Якщо ви проводите\(N\) ідентичні, статистично незалежні випробування, і ймовірність успіху в кожному дослідженні є\(P\), то в середньому загальна кількість успішних випробувань буде\(NP\). Якщо\(N\) вона досить велика, відносна похибка в цій оцінці стане невеликою.

Твердження про те, що правило обчислення середніх стає все більш точним для більших і більших\(N\) (відомий в народі як «закон середніх»), часто передбачає принцип відповідності, який з'єднує класичну і квантову фізику. Наприклад, кількість енергії, виробленої атомною електростанцією, не є випадковою на будь-якому виявленому рівні, оскільки кількість атомів у реакторі настільки велика. Загалом, випадкова поведінка на атомному рівні має тенденцію до усереднення, коли ми розглядаємо велику кількість атомів, саме тому фізика здавалася детермінованою до того, як фізики вивчали методи вивчення атомів окремо.

Ми можемо досягти великої точності за допомогою середніх показників квантової фізики, оскільки ми можемо використовувати однакові атоми для відтворення точно такої ж ситуації багато разів. Якби ми робили ставку на коней або кістки, ми були б набагато більш обмежені в нашій точності. Після тисячі забігів кінь була б готова піти на пенсію. Після мільйона кидків кістки будуть зношені.

Вправа\(\PageIndex{1}\)

Які з перерахованих речей повинні бути незалежними, які можуть бути незалежними, а які, безумовно, не є незалежними? (1) ймовірність успішного виконання двох штрафних кидків поспіль у баскетболі; (2) ймовірність того, що завтра в Лондоні піде дощ і ймовірність того, що в той же день у певному місті в далекій галактиці піде дощ; (3) ваша ймовірність померти сьогодні і померти завтра.

Відповідь

Відповідь у зворотному боці PDF-версії книги.

Вправа\(\PageIndex{1}\) Discussion Questions

Малюнок\(\PageIndex{3}\): Чому кістки випадкові?

• Ньютонівська фізика є по суті ідеальним наближенням для опису руху пари кубиків. Якщо ньютонівська фізика детермінована, чому ми вважаємо результат прокатки кубиків випадковим?
• Чому не вірно визначити випадковість, сказавши, що випадковість - це коли всі результати однаково вірогідні?
• Послідовність цифр 121212121212121212 здається явно невипадковою, а 41592653589793 здається випадковою. Остання послідовність, однак, є десятковою формою пі, починаючи з третьої цифри. Існує історія про індійського математика Рамануджана, вундеркінда самоучку, про те, що друг приїхав відвідати його в таксі, і зауважив, що номер кабіни, 1729, здавався відносно нецікавим. Рамануджан відповів, що навпаки, це дуже цікаво, оскільки це найменша кількість, яку можна було б представити двома різними способами як суму двох кубів. Аргентинський автор Хорхе Луїс Борхес написав коротку розповідь під назвою «Вавилонська бібліотека», в якій він уявив бібліотеку, що містить кожну книгу, яку можна було б написати за допомогою букв алфавіту. Вона включала б книгу, що містить лише повторювану букву «а»; всі давньогрецькі трагедії, відомі сьогодні, всі втрачені грецькі трагедії та мільйони грецьких трагедій, які ніколи насправді не були написані; ваша власна історія життя та різні неправильні версії вашої власної історії життя; і незліченні антології що містить короткий розповідь під назвою «Вавилонська бібліотека». Звичайно, якби ви вибрали книгу з полиць бібліотеки, то вона майже напевно виглядала б як безглузда послідовність букв і розділових знаків, але завжди можливо, що здавалося б безглуздою книгою був би науково-фантастичний сценарій, написаний мовою племені неандертальців, або лірика до набору незрівнянно красивих пісень про кохання, написаних мовою, яка ніколи не існувала. З огляду на ці приклади, що насправді означає сказати, що щось випадкове?

Відповідь

Додайте сюди тексти. Не видаляйте цей текст спочатку.

13.1.3 Розподіл ймовірностей

Поки ми обговорювали випадкові процеси, які мають лише два можливі результати: так чи ні, виграйте чи програйте, увімкнено чи вимкнено. Більш загально, випадковий процес може мати результат, який є числом. Деякі процеси дають цілі числа, як коли ви кидаєте плашку і отримуєте результат від одного до шести, але деякі не обмежуються цілими числами, наприклад, кількістю секунд, яке буде існувати атом урану-238 перед радіоактивним розпадом.

Розглянемо кидок плашки. Якщо померти «чесний», то ми очікуємо, що всі шість значень будуть однаково ймовірними. Оскільки всі шість ймовірностей повинні складати до 1, то ймовірність появи якогось конкретного значення повинна бути 1/6. Ми можемо підсумувати це на графіку (рис.\(\PageIndex{4a}\)). Області під кривою можна інтерпретувати як сумарні ймовірності. Наприклад, площа під кривою від 1 до 3 дорівнює\(1/6+1/6+1/6=1/2\), тому ймовірність отримання результату від 1 до 3 дорівнює 1/2. Функція, показана на графіку, називається розподілом ймовірностей.

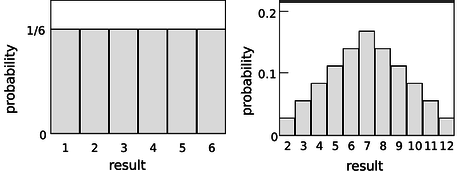
Рисунок\(\PageIndex{4}\): (а) Розподіл ймовірностей для результату прокатки однієї матриці. (б) Прокочування двох кубиків і складання їх.

\(\PageIndex{4b}\)На малюнку показані ймовірності різних результатів, отриманих при прокатці двох кубиків і складанні їх разом, як в грі в кістки. Ймовірності не всі однакові. Існує невелика ймовірність отримати двійку, наприклад, тому що є тільки один спосіб зробити це, прокотивши один, а потім інший. Імовірність прокатки сімки висока, оскільки існує шість різних способів зробити це: 1+6, 2+5 і т.д.

Якщо кількість можливих результатів велика, але кінцева, наприклад кількість волосків на собаці, графік почне виглядати як плавна крива, а не зигкурат.

Як щодо розподілу ймовірностей для випадкових чисел, які не є цілими числами? Ми більше не можемо зробити графік з ймовірністю на\(y\) осі, тому що ймовірність отримання заданого точного числа зазвичай дорівнює нулю. Наприклад, існує нульова ймовірність того, що радіоактивний атом триватиме рівно 3 секунди, оскільки існує нескінченно багато можливих результатів, близьких до 3, але не рівно трьох: наприклад, 2.999999999999999996876876587658465436. Тому зазвичай не має сенсу говорити про ймовірність одного числового результату, але є сенс говорити про ймовірність певного діапазону результатів. Наприклад, ймовірність того, що атом триватиме більше 3 і менше 4 секунд, є цілком розумною справою для обговорення. Ми все ще можемо узагальнити інформацію про ймовірності на графіку, і ми все ще можемо інтерпретувати області під кривою як ймовірності.

Але\(y\) ось вже не може бути безодиничною шкалою ймовірності. Наприклад, при радіоактивному розпаді ми хочемо, щоб\(x\) вісь мала одиниці часу, і ми хочемо, щоб області під кривою були безодиничними ймовірностями. Площа одного квадрата на графічному папері тоді

\[\begin{gather*} \text{(unitless area of a square)} \\ = \text{(width of square with time units)}\\ \times \text{(height of square)} . \end{gather*}\]

Якщо одиниці мають скасувати, то висота квадрата, очевидно, повинна бути величиною з одиницями зворотного часу. Іншими словами,\(y\) вісь графіка слід інтерпретувати як ймовірність за одиницю часу, а не ймовірність. \(\PageIndex{5}\)На малюнку показаний інший приклад, розподіл ймовірностей для зросту людей. Цей вид дзвіноподібної кривої досить поширений. \

Малюнок\(\PageIndex{5}\): Розподіл ймовірностей для зростання дорослих людей (не реальні дані).

Вправа\(\PageIndex{1}\)

Порівняйте кількість людей з ростом в діапазоні 130-135 см з числом в діапазоні 135-140

Відповідь

(Відповідь у зворотному боці PDF-версії книги).

Приклад\(\PageIndex{1}\): Looking for tall basketball players

Певна країна з великим населенням хоче знайти дуже високих людей, щоб бути в своїй олімпійській баскетбольній команді і завдати удару по західному імперіалізму. З басейну\(10^8\) людей, які належного віку та статі, скільки вони, ймовірно, знайдуть, хто має висоту понад 225 см (7 футів 4 дюйми)? Малюнок g дає крупний план «хвоста» розподілу, показаного раніше на малюнку\(\PageIndex{6}\).

Малюнок\(\PageIndex{6}\)

Затінена область під кривою представляє ймовірність того, що дана людина досить високий. Кожен прямокутник представляє ймовірність\(0.2\times10^{-7}\ \text{cm}^{-1} \times 1\ \text{cm}=2\times10^{-8}\). Є близько 35 прямокутників, покритих затіненою областю, тому ймовірність мати висоту більше 225 см становить\(7\times10^{-7}\), або трохи менше одного на мільйон. Використовуючи правило для обчислення середніх показників, середня або очікувана кількість людей, що мають такий зріст\((10^8)\times(7\times10^{-7})=70\).

Середнє значення та ширина розподілу ймовірностей

Якщо наступний марсіанин, якого ви зустрінете, запитає вас: «Наскільки висока доросла людина? ,» Ви, мабуть, відповісте заявою про середній зріст людини, наприклад, «О, близько 5 футів 6 дюймів». Якби ви хотіли пояснити трохи більше, ви могли б сказати: «Але це лише середнє значення. Більшість людей десь від 5 футів до 6 футів заввишки». Не турбуючись намалювати відповідну криву дзвінка для вашого нового позаземного знайомства, ви узагальнили відповідну інформацію, надавши середній та типовий діапазон варіацій.

Малюнок\(\PageIndex{6}\): Середнє значення розподілу ймовірностей.

Середнє значення розподілу ймовірностей можна визначити геометрично як горизонтальне положення, при якому воно може бути збалансоване, якби воно було побудовано з картону. Зручною чисельною мірою величини варіації щодо середнього, або величини невизначеності, є повна ширина на половині максимуму, або FWHM, показана на малюнку\(\PageIndex{7}\).

Малюнок\(\PageIndex{7}\): Повна ширина при половині максимуму (FWHM) розподілу ймовірностей.

Про цю тему можна сказати набагато більше, і справді вступний курс статистики може витратити місяці на способи визначення центру та ширини розподілу. Замість того, щоб примусово годувати вас математичними деталями або методами обчислення цих речей, можливо, більш актуально просто вказати на те, що існують різні способи їх визначення, і прищепити вас від неправильного використання певних визначень.

Середнє значення не є єдиним можливим способом сказати, що є типовим значенням для величини, яка може змінюватися випадковим чином; іншим можливим визначенням є медіана, визначена як значення, яке перевищено з ймовірністю 50%. При обговоренні доходів людей, які проживають в певному містечку, середній показник може бути вельми оманливим, так як на нього може вплинути масово, якщо єдиним жителем містечка буде Білл Гейтс. Також FWHM не є єдиним можливим способом визначення кількості випадкових варіацій; іншим можливим способом її вимірювання є стандартне відхилення (визначається як квадратний корінь середнього квадратного відхилення від середнього значення).

13.1.4 Експоненціальний розпад і період напіврозпаду

Більшість людей знають, що радіоактивність «триває певну кількість часу», але це просте твердження залишає багато. Як приклад розглянемо наступну медичну процедуру, яка використовується для діагностики функції щитовидної залози. Дуже невелика кількість ізотопу\(^{131}\text{I}\), виробленого в ядерному реакторі, подається або вводиться хворому. Біохімічні системи організму лікують цей штучний радіоактивний ізотоп точно так само\(^{127}\text{I}\), як, який є єдиним природним типом. (Харчово йод є необхідним мікроелементом. Прийнятий в організм йод частково виводиться, але решта стає концентрованим в щитовидній залозі. Йодована сіль додала до неї йод, щоб запобігти дефіциту харчування, відомому як зоби, при якому голодна йодом щитовидна залоза стає набряклою.) Коли\(^{131}\text{I}\) відбувається бета-розпад, він випромінює електрони, нейтрино та гамма-промені. Гамма-промені можна виміряти детектором, що проходить по тілу пацієнта. Оскільки радіоактивний йод концентрується в щитовидній залозі, кількість гамма-випромінювання, що надходить від щитовидної залози, стає більшою, а що викидається рештою тіла зменшується. Швидкість, з якою йод концентрується в щитовидній залозі, говорить лікарю про здоров'я щитовидної залози.

Якщо ви коли-небудь проходите цю процедуру, хтось, імовірно, трохи пояснить вам про радіоактивність, щоб розвіяти ваші страхи, що ви перетворитеся на Неймовірного Халка, або що ваша наступна дитина матиме незвичайну кількість кінцівок. Оскільки йод залишається у вашій щитовидній залозі протягом тривалого часу, як тільки вона потрапляє туди, одна річ, яку ви хочете знати, - чи буде ваша щитовидна залоза назавжди стати радіоактивною. Вони можуть просто сказати вам, що радіоактивність «триває лише певний проміжок часу», але тепер ми можемо провести кількісне виведення того, як радіоактивність дійсно згасне.

Нехай\(P_{surv}(t)\) буде ймовірність того, що атом йоду виживе, не розпадаючись хоча б на період\(t\). Експериментально виміряно, що половина всіх\(^{131}\text{I}\) атомів розпадається за 8 годин, тому ми маємо

\[ P_{surv}(8\ \text{hr}) = 0.5 . \]

Тепер, використовуючи закон незалежних ймовірностей, ймовірність вижити протягом 16 годин дорівнює ймовірності вижити за перші 8 годин, помноженої на ймовірність вижити за другі 8 годин,

\[\begin{align*} P_{surv}(16\ \text{hr}) &= 0.50\times0.50 \\ &= 0.25 . \end{align*}\]

Аналогічно у нас

\[\begin{align*} P_{surv}(24\ \text{hr}) &= 0.50\times0.5\times0.5 \\ &= 0.125 . \end{align*}\]

Узагальнюючи з цієї закономірності, ймовірність вижити за будь-який час\(t\), кратний 8 годинам, дорівнює

\[ P_{surv}(t) = 0.5^{t/8\ \text{hr}} . \]

Тепер ми знаємо, як знайти ймовірність виживання з інтервалом в 8 годин, але як щодо точок часу між ними? Якою була б ймовірність вижити протягом 4 годин? Ну, використовуючи знову закон незалежних ймовірностей, ми маємо

\[ P_{surv}(8\ \text{hr}) = P_{surv}(4\ \text{hr}) \times P_{surv}(4\ \text{hr}) , \]

які можна переставити, щоб дати

\[\begin{align*} P_{surv}(4\ \text{hr}) &= \sqrt{P_{surv}(8\ \text{hr})} \\ &= \sqrt{0.5} \\ &= 0.707 . \end{align*}\]

Це саме те, що ми б знайшли, просто підключивши\(P_{surv}(t)=0.5^{t/8\ \text{hr}}\) та ігноруючи обмеження кратними 8 годинам. Оскільки 8 годин - це кількість часу, необхідного для розпаду половини атомів, він відомий як період напіврозпаду, написаний\(t_{1/2}\). Загальне правило полягає в наступному:

\[ \underbrace{P_{surv}(t) = 0.5^{t/t_{1/2}}}_{\text{Exponential Decay Equation}} \]

Використовуючи правило обчислення середніх, ми також можемо знайти кількість атомів\(N(t)\), що залишилися в вибірці за часом\(t \):

\[ N(t) = N(0) \times 0.5^{t/t_{1/2}} \]

Обидва ці рівняння мають графіки, які виглядають як вимираючі експоненціальні, як у прикладі нижче.

Приклад\(\PageIndex{2}\): Radioactive contamination at Chernobyl

Одним з найнебезпечніших радіоактивних ізотопів, випущених в результаті Чорнобильської катастрофи в 1986 році\(^{90}\text{Sr}\), період напіврозпаду якого становить 28 років. (a) Скільки часу пройде, перш ніж забруднення зменшиться до однієї десятої від початкового рівня? (b) Якби було вивільнено загалом\(10^{27}\) атомів, приблизно скільки часу було б до того, як не залишилося жодного атома?

Рішення

(a) Ми хочемо знати кількість часу, який\(^{90}\text{Sr}\) ядро має ймовірність 0,1 виживання. Починаючи з формули експоненціального розпаду,

\[ P_{surv} = 0.5^{t/t_{1/2}} , \nonumber \]

ми хочемо вирішити для\(t\). Беручи натуральні логарифми обох сторін,

\[ \ln P = \frac{t}{t_{1/2}}\ln 0.5 , \nonumber\]

тому

\[ t = \frac{t_{1/2}}{\ln 0.5}\ln P \nonumber \]

Підключивши\(P=0.1\) і\(t_{1/2}=28\) роки, ми отримуємо\(t=93\) роки.

(б) Це так само, як і перша частина, але\(P=10^{-27}\). Результат - близько 2500 років.

Приклад\(\PageIndex{3}\): \(^{14}\text{C}\) Dating

Майже весь вуглець на Землі є\(^{12}\text{C}\), але не зовсім. Ізотоп\(^{14}\text{C}\), з періодом напіврозпаду 5600 років, виробляється космічними променями в атмосфері. Він розпадається природним шляхом, але заповнюється з такою швидкістю, що частка\(^{14}\text{C}\) в атмосфері залишається постійною, при\(1.3\times10^{-12}\). Живі рослини та тварини приймають як, так\(^{12}\text{C}\) і\(^{14}\text{C}\) з атмосфери і включають обидва в своє тіло. Як тільки живий організм помирає, він більше не приймає атоми С з атмосфери, і частка\(^{14}\text{C}\) поступово падає, оскільки він зазнає радіоактивного розпаду. Цей ефект може бути використаний для пошуку віку мертвих організмів, або людських артефактів, виготовлених з рослин або тварин. На малюнку j показана експоненціальна крива розпаду\(^{14}\text{C}\) в різних об'єктах. Подібні методи, використовуючи довгоживучі ізотопи, надали перший твердий доказ того, що землі було мільярди років, а не кілька тисяч, як деякі стверджували за релігійними ознаками.

Малюнок\(\PageIndex{8}\): Калібрування методу\(^{14}\text{C}\) датування з використанням кілець дерев і артефактів, вік яких був відомий з інших методів. Перераховано з Еміліо Сегре, Ядра та частинки, 1965.

Швидкість розпаду

Якщо ви хочете знайти, скільки радіоактивних розпадів відбувається протягом часового інтервалу, що триває час\(t\) від часу\(t+\Delta t\), найбільш простий підхід полягає в тому, щоб обчислити це так:

\[\begin{align*} (\text{number of}&\text{ decays between } t \text{ and } t+\Delta t) \\ &= N(t) - N(t+\Delta t) \end{align*}\]

Зазвичай нас цікавить випадок, коли\(\Delta t\) є малим порівняно з\(t_{1/2}\), і в цьому обмеженому випадку обчислення починає виглядати точно так само, як межа, яка йде у визначення похідної\(dN/dt\). Тому зручніше говорити про швидкість розпаду,\(-dN/dt\) а не про кількість розпадів в якомусь скінченному часовому інтервалі. Робити обчислення на функції також\(e^x\) простіше, ніж з\(0.5^x\), тому ми переписуємо функцію\(N(t)\) як

\[ N = N(0) e^{-t/\tau} , \]

де\(\tau=t_{1/2}/\ln 2\) показано в прикладі 6 на стор. 835, щоб бути середнім часом виживання. Швидкість розпаду тоді

\[ -\frac{dN}{dt} = \frac{N(0)}{\tau} e^{-t/\tau} . \]

Математично, диференціація експоненціальної просто повертає ще одну експоненціальну. Фізично це говорить нам про те, що коли\(N\) випадає експоненціально, швидкість розпаду падає з тією ж експоненціальною швидкістю, оскільки нижча\(N\) означає меншу кількість атомів, які залишаються доступними для розпаду.

Вправа\(\PageIndex{1}\)

Перевірте, щоб обидві сторони рівняння швидкості розпаду мали одиниці\(\text{s}^{-1}\), тобто розпаду за одиницю часу.

Відповідь

відповідь в зворотному боці PDF-версії книги)

Приклад\(\PageIndex{4}\): The hot potato

Ядерний фізик з божевільним почуттям гумору кидає вам сигарну коробку, кричачи «гаряча картопля». На етикетці на коробці написано «містить\(10^{20}\) атоми\(^{17}\text{F}\), період напіврозпаду 66 с, вироблених сьогодні в нашому реакторі о 13:00». У вас буде потрібно дві секунди, щоб прочитати етикетку, після чого ви кидаєте його за кілька свинцевих цегли і тікаєте. Час 13:40 Ви помрете?

Рішення

Час, що минув з моменту отримання радіоактивного фтору в реакторі, становив 40 хвилин, або 2400 с, отже, кількість минулих періодів напіврозпаду становить\(t/t_{1/2}= 36\). Початкове число атомів було\(N(0)=10^{20}\). Кількість розпадів в секунду зараз приблизно\(10^7\ \text{s}^{-1}\), тому він виробляв близько\(2\times10^7\) високоенергетичних електронів, поки ви тримали його в руках. Хоча двадцять мільйонів електронів звучить як багато, насправді недостатньо, щоб бути небезпечним.

До речі, жодне з рівнянь, які ми вивели до цих пір, не було фактичним розподілом ймовірностей за час, коли той чи інший радіоактивний атом розпадається. Цей розподіл ймовірностей буде знайдений шляхом підстановки\(N(0)=1\) в рівняння швидкості розпаду.

Питання для обговорення

◊ У медичній процедурі за участю\(^{131}\text{I}\), чому виявляються гамма-промені, а не електрони або нейтрино, які також випромінюються?

◊ Протягом 1 с Фред тримає в руках 1 кг радіоактивного матеріалу з періодом напіврозпаду 1000 років. Імбир утримує 1 кг іншої речовини, з періодом напіввиведення 1 хв, за таку ж кількість часу. Чи ставили вони себе в рівну небезпеку, чи ні?

◊ Як би ви це інтерпретували, якби розрахували\(N(t)\), і виявили, що це менше одиниці?

◊ Чи залежить період напіврозпаду від того, скільки речовини у вас є? Чи залежить очікуваний час до повного розпаду зразка від того, скільки речовини у вас є?

13.1.5 Застосування обчислення

Площа під розподілом ймовірностей, звичайно, є невід'ємною частиною. Якщо називати випадкове число\(x\) і розподіл ймовірностей\(D(x)\), то ймовірність, що\(x\) лежить в певному діапазоні, задається

\[ \text{(probability of $a\le x \le b$)}=\int_a^b D(x) dx . \]

А як щодо середніх? \(x\)Якби було кінцеве число однаково ймовірних значень, ми б просто склали їх і розділили на те, скільки у нас було. Якби вони не були однаково ймовірними, ми б зробили середньозважене\(x_1P_1+x_2P_2+\)... Але ми повинні узагальнити це до змінної\(x\), яка може взяти на себе будь-який з континууму значень. Безперервний варіант суми є інтегралом, тому середнє значення

\[ \text{(average value of $x$)} = \int x D(x) dx , \]

де інтеграл знаходиться над усіма можливими значеннями\(x\).

Приклад\(\PageIndex{5}\): Probability distribution for radioactive decay

Ось суворе обґрунтування твердження в підрозділі 13.1.4 про те, що розподіл ймовірностей радіоактивного розпаду виявляється шляхом підстановки\(N(0)=1\) в рівняння швидкості розпаду. Ми знаємо, що розподіл ймовірностей повинен мати вигляд

\[ D(t) = k 0.5^{t/t_{1/2}} , \]

де\(k\) константа, яку нам потрібно визначити. Атом гарантовано розпадається з часом, тому нормалізація дає нам

\[\begin{align*} \text{(probability of $0\le t \lt \infty$)} &= 1 \\ &= \int_0^\infty D(t) dt . \end{align*}\]

Інтеграл найбільш легко оцінюється шляхом перетворення функції в експоненціальну з\(e\) основою

\[\begin{align*} D(t) &= k \exp\left[\ln\left(0.5^{t/t_{1/2}}\right)\right] \\ &= k \exp\left[\frac{t}{t_{1/2}}\ln 0.5\right] \\ &= k \exp\left(-\frac{\ln 2}{t_{1/2}}t\right) , \end{align*}\]

що дає інтеграл звичної форми\(\int e^{cx}dx=(1/c)e^{cx}\). Таким чином, ми маємо

\[ 1 = \left.-\frac{kt_{1/2}}{\ln 2}\exp\left(-\frac{\ln 2}{t_{1/2}}t\right)\right]_0^\infty , \]

що дає бажаний результат:

\[ k = \frac{\ln 2}{t_{1/2}} . \]

Приклад\(\PageIndex{6}\): Average lifetime

Ви можете подумати, що період напіврозпаду також буде середнім терміном життя атома, оскільки половина життя атомів коротше і наполовину довше. Але половина життя яких довша, включають деякі, які виживають протягом багатьох періодів напіврозпаду, і ці рідкісні довгоживучі атоми перекошують середнє. Ми можемо розрахувати середній термін служби наступним чином:

\[ (\text{average lifetime}) = \int_0^\infty t\: D(t)dt \]

Використовуючи зручну\(e\) base-форму знову, ми маємо

\[ (\text{average lifetime}) = \frac{\ln 2}{t_{1/2}} \int_0^\infty t \exp\left(-\frac{\ln 2}{t_{1/2}}t\right) dt . \]

Цей інтеграл має форму, яка може бути атакована інтеграцією частинами або дивлячись його в таблиці. Результат є\(\int x e^{cx}dx=\frac{x}{c}e^{cx}-\frac{1}{c^2}e^{cx}\), і перший термін можна проігнорувати для наших цілей, оскільки він дорівнює нулю в обох межах інтеграції. Ми закінчуємо

\[\begin{align*} \text{(average lifetime)} &= \frac{\ln 2}{t_{1/2}}\left(\frac{t_{1/2}}{\ln 2}\right)^2 \\ &= \frac{t_{1/2}}{\ln 2} \\ &= 1.443 \: t_{1/2} , \end{align*}\]

який, як і очікувалося, довше одного періоду напіврозпаду.

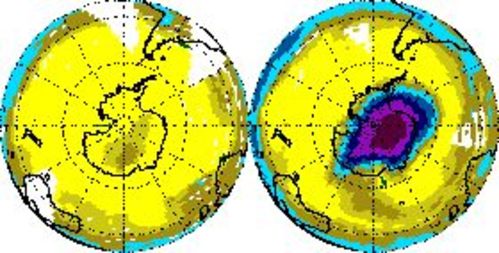
Малюнок\(\PageIndex{9}\): В останні десятиліття величезна діра в озоновому шарі поширилася з Антарктиди. Залишилося: листопад 1978 р. Праворуч: Листопад 1992

Автори та атрибуція

• Template:ContribCrowell