9.3: Хаос у гамільтонових системах

Останній висновок, звичайно, справедливий для гамільтонових систем, які є лише певним типом динамічних систем. Однак можна задатися питанням, чи можуть ці системи, які мають принаймні один перший інтеграл руху,\(H=\) const, а отже, більш «впорядковані», ніж системи, розглянуті вище, демонструвати хаос взагалі. Відповідь так, тому що такі системи все ще можуть мати механізми експоненціального зростання невеликого початкового збурень.

Як найпростіший спосіб його показати розглянемо так званий математичний більярд, тобто систему з балістичною частинкою («кулькою»), вільно рухається за інерцією по горизонтальній площині поверхні («столу»), обмеженої жорсткими непроникними стінками. У цій ідеалізованій моделі звичайної гри в більярд швидкість кулі\(\mathbf{v}\) зберігається, коли він рухається по столу, а коли він набігає в стіну, м'яч пружно відбивається від нього, як від дзеркала,\({ }^{14}\) з розворотом знака нормальної швидкості\(v_{n}\), а збереження тангенціальної швидкості\(v_{\tau}\), а отже, без втрати її кінетичної (а отже і повної) енергії\[E=H=T=\frac{m}{2} v^{2}=\frac{m}{2}\left(v_{n}^{2}+v_{\tau}^{2}\right) .\] Ця модель, будучи законною\(2 \mathrm{D}\) динамічною системою,\({ }^{15}\) дозволяє проводити геометричний аналіз для декількох простих форм таблиці. Найпростіший випадок - це прямокутний більярд площі\(a \times b\) (рис. 7), аналіз якого може бути легко здійснений лише заміною кожної події відображення кулі на дзеркальне відображення столу в тій стіні - див. Пунктирні лінії на панелі (а).

Малюнок 9.7. Рух кулі на прямокутному більярді при (а) співмірному, і (б) непорівнянному куті запуску.

Такий аналіз (залишився на задоволення читача: -) показує, що якщо тангенс кута запуску кулі співмірний співвідношенню довжини сторони:\[\tan \varphi=\pm \frac{m}{n} \frac{b}{a},\] де\(n\) і\(\varphi\)\(m\) є невід'ємними цілими числами без загальних цілих множників, куля повертається точно до точки запуску \(\mathrm{O}\), Після\(m\) відскакування разів від кожної стіни довжини\(a\), і\(n\) раз від кожної стіни довжини\(b\). (Червоні лінії на малюнку 7а показують приклад такої траєкторії для\(n=m=1\), в той час як сині лінії, для\(m=3, n=1 .\)) Чим більше сума\((m+n)\), тим складніше така замкнута траєкторія - «орбіта». Нарешті, якщо\((n+m) \rightarrow \infty\), тобто\(\tan \varphi\) і\(b / a\) несумірні (мається на увазі, що їх співвідношення є ірраціональним числом), траєкторія охоплює всю площу столу, і м'яч ніколи не повертається точно в точку запуску. Тим не менш, це не справжній хаос. Дійсно, невеликий зсув точки запуску\(\mathrm{O}\) зміщує всі фрагменти траєкторії на однакове зміщення. Більш того, в будь-який момент\(t\) кожна з\(v_{j}(t)\) декартових складових швидкості кулі (з координатними осями, паралельними сторонам таблиці) може приймати тільки два значення\(\pm v_{j}(0)\), а значить може змінюватися лише стільки, скільки змінюється початкова швидкість.

У 1963 році, тобто задовго до роботи Е.Лоренца, Яків Синай показав, що ситуація повністю змінюється, якщо в прямокутний більярд вставити додаткову стіну, у формі кола (рис. 8). Для більшості початкових умов траєкторія кулі врешті-решт потрапляє в коло (див. Червону лінію на панелі (а) як приклад), і подальша траєкторія стає по суті хаотичною. Дійсно, розглянемо відображення кулі від округлоподібної стіни - рис. 8б. Завдяки збереженню тангенціальної швидкості, і знакової зміни нормальної швидкісної складової, відображення підпорядковується простому закону:\(\theta_{\mathrm{r}}=\theta_{1}\). \(8 \mathrm{~b}\)На малюнку видно, що в результаті величина невеликої різниці\(\delta \varphi\) між кутами двох близьких траєкторій (як вимірюється в лабораторній системі), подвоюється при кожному відображенні від криволінійної стіни. Це означає, що невелике відхилення зростає вздовж траєкторії кулі, як\[|\delta \varphi(N)| \sim|\delta \varphi(0)| \times 2^{N} \equiv|\delta \varphi(0)| e^{N \ln 2},\] де\(N\) знаходиться кількість відбитків від опуклої стінки. \({ }^{16}\)Як ми вже знаємо, така експоненціальна розбіжність траєкторій, з позитивним показником Ляпунова, є головною рисою детермінованого хаосу. \({ }^{17}\)

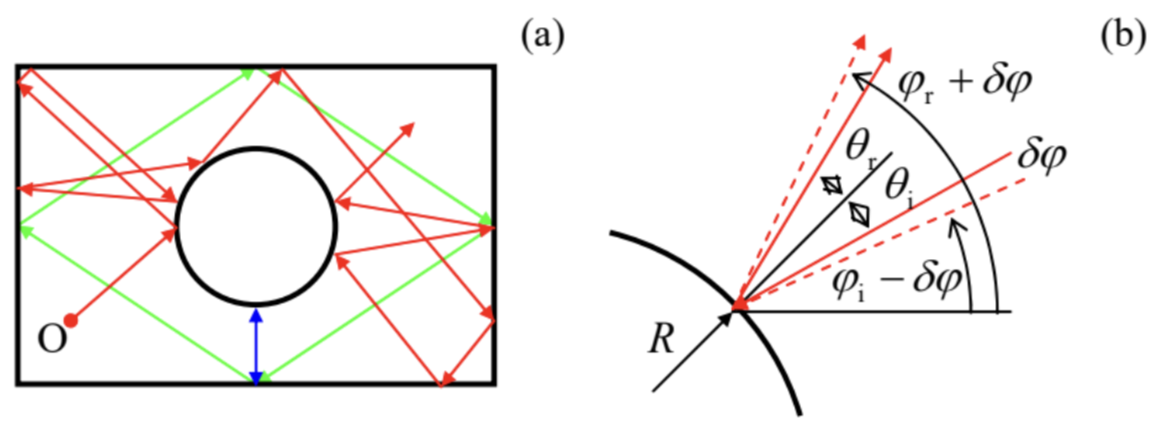Малюнок 9.8. (а) Рух на синайському більярдному столі та (б) механізм експоненціальної розбіжності тісних траєкторій.

Найважливішою новою особливістю динамічного хаосу в гамільтонових системах є його залежність від початкових умов. (У системах, розглянутих в попередніх двох попередніх розділах, в яких відсутні інтеграли руху, початкові умови швидко «забуваються», а хаос зазвичай характеризується після початкового перехідного періоду - див., наприклад, рис. 4.) Дійсно, навіть синайський більярд допускає періодичний рух, по замкнутих орбітах, при певних початкових умовах - дивіться сині та зелені лінії на малюнку 8а як приклади. Таким чином, «глибина» хаосу в таких системах може характеризуватися «фракцією» 18 фазового простору початкових параметрів (для 2D більярду, 3D простору початкових значень\(x, y\), і\(\varphi\)), що призводить до хаотичних траєкторій.

Цей висновок справедливий і для гамільтонових систем, які зустрічаються в експерименті частіше, ніж більярд, наприклад, зв'язані нелінійні осцилятори без демпфування. Мабуть, найбільш раннім і найпопулярнішим прикладом є так звана система Енона-Хейля,\({ }^{19}\) яку можна описати наступною функцією Лагранжа:\[L=\frac{m_{1}}{2}\left(\dot{q}_{1}^{2}-\omega_{1}^{2} q_{1}^{2}\right)+\frac{m_{2}}{2}\left(\dot{q}_{2}^{2}-\omega_{2}^{2} q_{2}^{2}\right)-\varepsilon\left(q_{1}^{2}-\frac{1}{3} q_{2}^{2}\right) q_{2} .\]\[\begin{aligned} &m_{1}\left(\ddot{q}_{1}+\omega_{1}^{2} q_{1}\right)=-2 \varepsilon q_{1} q_{2}, \\ &m_{2}\left(\ddot{q}_{2}+\omega_{2}^{2} q_{2}\right)=-\varepsilon\left(q_{1}^{2}-q_{2}^{2}\right), \end{aligned}\] і знайти свій перший інтеграл руху (фізично, закон енергозбереження):\[H=E=\frac{m_{1}}{2}\left(\dot{q}_{1}^{2}+\omega_{1}^{2} q_{1}^{2}\right)+\frac{m_{2}}{2}\left(\dot{q}_{2}^{2}+\omega_{2}^{2} q_{2}^{2}\right)+\varepsilon\left(q_{1}^{2}-\frac{1}{3} q_{2}^{2}\right) q_{2}=\text { const . }\] У контексті наших дискусій у розділах 5 та 6, Eqs. (19) можна легко інтерпретувати як ті, що описують два осцилятори, з малими частотами коливань\(\omega_{1}\) і\(\omega_{2}\), з'єднані лише так, як описано квадратичними термінами на правій стороні рівнянь. Це означає, що оскільки амплітуди коливань\(A_{1,2}\), а отже і повна енергія\(E\) системи, близькі до нуля, підсистеми осциляторів практично незалежні, кожна з яких виконує синусоїдальні коливання на своїй частоті. Це спостереження передбачає зручний спосіб зобразити рух системи. \({ }^{20}\)Розглянемо площину Пуанкаре для одного з осциляторів (скажімо, з координатою\(q_{2}\)), подібну до тієї, що розглядається в п. 2 вище, з тією лише різницею, що (через відсутність явної функції часу в рівняннях системи) траєкторія на фазовій площині \(\left[q_{2}, \dot{q}_{2}\right]\)виділяється в моменти, коли\(q_{1}=0\).

Почнемо з межі\(A_{1,2} \rightarrow 0\), коли коливання\(q_{2}\) практично синусоїдальні. Як ми вже знаємо (див. Рисунок\(5.9\) та його обговорення), якби підсвічування точки представлення була ідеально синхронною з частотою\(\omega_{2}\) коливань, на площині Пуанкаре була б лише одна точка - див., наприклад, праву верхню панель малюнка 4. Однак при\(q_{1}\) - ініційованому підсвічуванні немає такого синхронності, так що кожен період виділяється різна точка еліптичної (при правильному масштабуванні швидкості, кругової) траєкторії, так що отримані точки при певних початкових умовах перебувають на колі радіуса \(A_{2}\). Якщо тепер змінити початкові умови, тобто перерозподілити початкову енергію між осциляторами, але зберегти загальну енергію\(E\) постійною, на площині Пуанкаре ми отримаємо набір еліпсів.

Тепер, якщо початкова енергія збільшена, нелінійна взаємодія коливань починає деформувати ці еліпси, викликаючи також їх перетину - див., наприклад, верхню ліву панель малюнка 9. Тим не менш, нижче певного порогового значення\(E\), всі точки Пуанкаре, що належать до певної початкової умови, сидять на одному замкнутому контурі. Причому ці контури можуть бути розраховані приблизно, але з досить хорошою точністю, використовуючи прямолінійне узагальнення методу, розглянутого в п. 5.2.21

Малюнок 9.9. Площини Пуанкаре системи Енонгейля (19) у\(y \equiv \varepsilon q_{2}\) позначеннях для трьох значень безрозмірної енергії\(e \equiv E / E_{0}\), с\(E_{0} \equiv m_{1} \omega_{1}{ }^{2} / \varepsilon^{2}\). Адаптовано з М. Енон і К. Хейлес, Астрон. Дж.\(\mathbf{6 9}, 73\) (1964). \ odot AAS, відтворюється з дозволу.

Однак, починаючи з деякого значення енергії, певні початкові умови призводять до послідовностей точок, розкиданих по частинам площини Пуанкаре, з ненульовою площею - див. Верхню праву панель малюнка.\(9 .\) Це означає, що відповідні коливання\(q_{2}(t)\) не повторюються від одного (квазі-) періоду до наступний\(-\) пор рис. 4 для дисипативного, примусового маятника. Це хаос. \({ }^{22}\)Однак деякі інші початкові умови все ж призводять до замкнутих контурів. Ця особливість схожа з такою в синайському більярді, і характерна для гамільтонових систем. У міру збільшення енергії більші і більші частини площини Пуанкаре відповідають хаотичному руху, що означає більш глибокий і глибший хаос - див. Нижню панель малюнка 9.

---

\({ }^{14}\)Більш науково-звучне назва такого відображення - дзеркально-від латинського слова «speculum», що означає металеве дзеркало.

\({ }^{15}\)Дійсно, вона повністю описується наступною функцією Лагранжа:\(L=m v^{2} / 2-U(\rho)\), з\(U(\rho)=0\) для\(2 \mathrm{D}\) радіусних векторів,\(\rho\) що належать до площі таблиці, і\(U(\rho)=+\infty\) поза площею.

\({ }^{16}\)Поверхнево, Eq. (17) також справедливо для плоской стіни, але, як було розглянуто вище, більярд з такими стінами має повну кореляцію між послідовними відображеннями, так що кут\(\varphi\) завжди повертається до свого початкового значення. У синайському більярді така кореляція зникає. Увігнуті стіни також можуть зробити більярд хаотичним; відомий приклад - стадіонний більярд, запропонований Леонідом Бунімовичем в 1974 році, з двома прямими паралельними стінами, що з'єднують дві напівкруглі увігнуті стіни. Іншим прикладом, який дозволяє простий аналіз (вперше проведений Мартіном Гутсвіллером у 1980-х роках), є так званий більярд Адамара: нескінченний (або прямокутний) стіл з негоризонтальною поверхнею негативної кривизни.

\({ }^{17}\)Більярд з вигнутими стінами також є зручною платформою для вивчення квантових властивостей класично хаотичних систем (для їх концептуального обговорення див. QM Sec. 3.5), зокрема, особливості, які називаються «квантовими шрамами», див., наприклад, вражаючі результати чисельного моделювання Е.Хеллера, Phys. Преподобний Летт. \(\mathbf{5 3}, 1515\)(1984).

\({ }^{18}\)Власне, кількісна характеристика дробу не є тривіальною, оскільки вона може мати фрактальну розмірність. На жаль, через брак часу мені доводиться направляти зацікавленого в цьому питанні читача до спеціальної літератури, наприклад, монографії Б.Мандельброта (цитується вище) та посилань на неї.

\({ }^{19}\)Вперше вона була вивчена в 1964 році Мішелем Еноном і Карлом Хайлесом як проста модель обертання зірки навколо галактичного центру. Більшість досліджень цього рівняння були проведені для наступного конкретного випадку:\(m_{2}=2 m_{1}, m_{1} \omega_{1}{ }^{2}=\)\(m_{2} \omega_{2}{ }^{2}\). У цьому випадку, введення нових змінних\(x \equiv \varepsilon q_{1}, y \equiv \varepsilon q_{2}\), причому\(\tau \equiv \omega_{1} t\), є можливість переписати Eqs. (18) - (20) в безпараметричних формах. Всі результати, показані на малюнку 9 нижче, призначені для цього випадку.

\({ }^{20}\)Як правило, система має траєкторію в 4D просторі, наприклад, координати\(q_{1,2}\) та їх похідні від часу, хоча перший інтеграл руху (20) означає\(E\), що для кожної фіксованої енергії рух обмежується тривимірним підпростором. Тим не менш, це один вимір занадто багато для зручного подання руху.

\({ }^{21}\)Див., наприклад, М.Беррі, в: С.Джорна (ред.), Теми в нелінійній динаміці, AIP Conf. Проц. № 46, АІП, 1978, с. 16-120.

\({ }^{22}\)Цей факт відповідає необхідній умові хаосу, обговорюваному в кінці секції 2, оскільки Eqs. (19) можуть бути переписані як система з чотирьох диференціальних рівнянь першого порядку.