7.2: Опір повітря, пропорційний швидкості

Як і в попередньому розділі, я напишу$x$ -компонент рівняння руху, і першого і другого часу інтегралів, в лівій колонці, і$y$ -компонент в правій колонці. $x$-складова опору повітря на одиницю маси є$\gamma\dot{x}$ і$y$ -компонент є$\gamma\dot{y}$. $\gamma$Ось константа демпфування, визначена в розділі 6.3. У$x$ - і$y$ -складових початкової швидкості є, відповідно,$V_{0} \cos \alpha$ і$V_{0} \sin \alpha$. Слід легко бачити, що рівняння руху та їх тимчасові інтеграли такі:

Горизонтальний	Вертикальний
$\ddot{x} = -\gamma\dot{x}$	$\ddot{y} = -g-\gamma\dot{y}$	$7.2.1a,b$
$\dot{x} = u = V_{0}\cos\alpha.e^{-\gamma t}$	$\dot{y}= v= V_0 \sin \alpha e^{-\gamma t} -\hat{v}(1-e^{\gamma t} ) \\ \text{where} \, \hat{v} = g/\gamma$	$7.2.2a,b$
$x=x_\infty\left(1 - e^{-\gamma t}\right)\\ \text{where}\space x_{\infty} = \frac{V_0 \cos \alpha}{\gamma}$	$y = \dfrac{1}{\gamma}(V_{0}\sin \alpha + \hat{v})(1-e^{-\gamma t})- \hat{v}t$	$7.2.3a,b$

(Якщо це не «легко видно», для горизонтального руху зверніться до розділу 3 глави 6, особливо Рівняння 6.3.2, 6.3.3 та 6.3.5, а для вертикального руху зверніться до розділу 6, розділ 3b, особливо Рівняння 6.3.24, 6.3.25 та 6.3.27.) Буде видно, що$t\rightarrow\infty$,$u\rightarrow0$,$v\rightarrow -\hat{v}$,$x\rightarrow x_{\infty}$. $xy$-рівняння до траєкторії є$t$ -елімінант рівнянь$6.2.3a$ і$6.2.3b$. Після невеликої кількості алгебри це виявляється:

$$y=\dfrac{x(V_{0}\sin\alpha+\hat{v})}{V_{0}\cos\alpha} + \dfrac{\hat{v}}{\gamma}\ln \left(1-\dfrac{x}{x_{\infty}}\right). \tag{7.2.4}\label{eq:7.2.4}$$

Діапазон на горизонтальній площині знаходить, встановивши$y$ = 0, щоб отримати або

$$x = -Aln(1-\frac{x}{x_{\infty}}) \tag{7.2.5}\label{eq:7.2.5}$$

або

$$x = {x_{\infty}}(1-e^{-\frac{x}{A}}), \tag{7.2.6}\label{eq:7.2.6}$$

де

$$A=\frac{\hat{v}V_{0}cos\alpha}{\gamma(V_{0}sin\alpha+\hat{v})},x_{\infty}=\frac{V_{0}cos\alpha}{\gamma} \nonumber$$

і

$$\hat{v}=\frac{g}{\gamma}. \nonumber$$

Приклад$\PageIndex{1}$

Припустимо

• $V_{0}$= 20 мс ^-1
• $\alpha$= 50$^{\circ}$
• $g$=9.8 мс ^-2
• $\gamma$=1.96с ^-1 ($\therefore\hat{v}$=5 мс ⁻¹)

Тоді$A$ = 1,613 870 65 м

а$x_{\infty}$ = 6,55905724 м.

Спробуйте знайти діапазон на горизонтальній площині, використовуючи$\ref{eq:7.2.5}$ або Рівняння$\ref{eq:7.2.6}$, або, до дев'яти значущих цифр. Яке рівняння найкраще працює? Ньютон-Рафсон може провалитися з дурною першою здогадкою - але зробити досить розумну першу здогадку не повинно бути важко. Не повинен вам розповідати, але цифра VII.2 була розрахована за даними цього прикладу.

Я роблю відповідь 6.437 584 2 м.

Ось більш складна проблема.

Приклад$\PageIndex{2}$

Загальновідомо, що при відсутності опору повітря максимальний діапазон на горизонтальній площині здійснюється шляхом вибору початкової висоти запуску, щоб бути$\alpha$ = 45$^{\circ}$. Що робити, якщо є опір повітря, з постійною демпфуванням$\gamma$? Яким же тоді повинен бути кут запуску для досягнення найбільшої дальності на горизонтальній площині? Дано рівняння$\ref{eq:7.2.6}$$x=x_{\infty}(1-e^{\frac{-x}{A}})$, для якого значення$\alpha$ є$x$ найбільшим?

Рішення

Рівняння$\ref{eq:7.2.6}$, записане повністю, є

$$x=\frac{V_{0}cos\alpha}{\gamma}\left[1-exp\left(\frac{-\gamma(V_{0}\sin\alpha+\hat{v})x}{\hat{v}V_{0}\cos\alpha}\right)\right]. \tag{7.2.7}\label{eq:7.2.7}$$

Це можна написати

$$x=acos\alpha\left[1-exp\left(-\frac{(b \sin\alpha + 1)x}{a \cos\alpha}\right)\right], \tag{7.2.8}\label{eq:7.2.8}$$

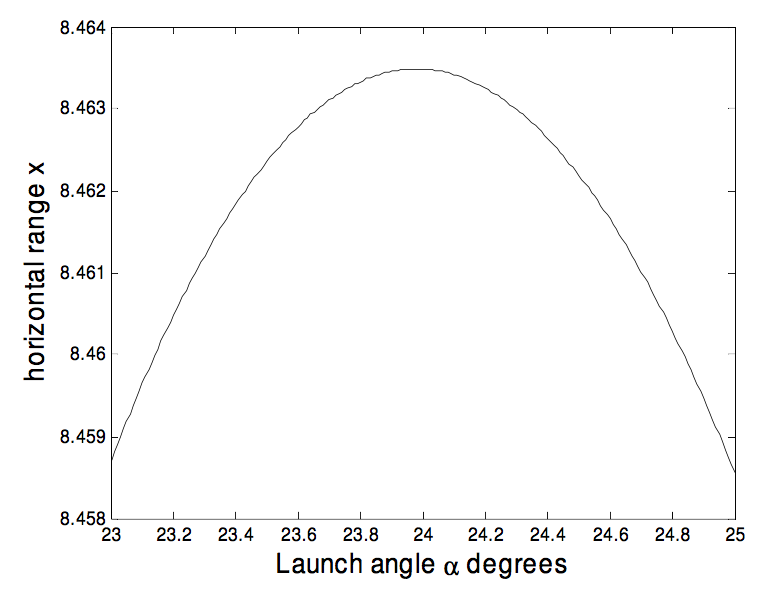
де$a=\frac{V_{0}}{\gamma}$ і$b=\frac{V_{0}}{\hat{v}}=\frac{\gamma V_{0}}{g}$. Ми повинні знайти, для чого значення$\alpha$ є$x$ найбільшим. Це здається досить простою проблемою, але на даний момент я не можу знайти хорошого способу її вирішення. Якщо у когось є підказка, дайте мені знати ([e-mail]). Тим часом найкраще, що я можу запропонувати, для нашого конкретного числового прикладу, обчислити діапазон$x$, для декількох значень$\alpha$ і побачити, де він проходить максимум. Для нашого конкретного числового прикладу,$a$ = 10,204 081 63 м і$b$ = 4. Ось графік діапазону проти кута запуску, для початкової швидкості 20 мс ⁻¹. Кут запуску близько 23$^{\circ}$ 59′ дає дальність близько 8.4635 м Для заданого$\gamma$ і$g$, оптимальний кут запуску залежить від швидкості запуску$V_{0}$. Це інтуїтивно очевидно?