5.5: Косі (поглядові) пружні зіткнення, альтернативне лікування

На малюнку V.3, на відміну від малюнка V.2, горизонтальна лінія не призначена для представлення лінії центрів. Швидше, це напрямок початкової швидкості\( m_{1}\), і спочатку\( m_{2}\) знаходиться в стані спокою. Друга \( m_{2}\)маса трохи відходить від лінії швидкості\( m_{1}\). Я припускаю, що зіткнення еластичне, так що\( e = 1\). У частині «перед» малюнка я вказав, а також дві маси, положення і швидкість\( \bf{V}\) центру мас\( C\). Швидкість руху\( C\) залишається постійною, тому що зовнішніх сил на систему немає. Я не малював\( C\) в «після» частини Фігури, тому що це трохи заважало б. Подумайте, де він знаходиться.

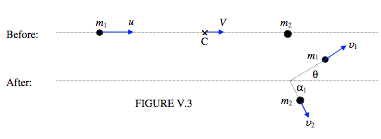
На малюнку V.3 показана ситуація в «лабораторному просторі». (Пізніше ми розглянемо ситуацію, пов'язану з еталонним кадром, в якому\( C\) знаходиться в стані спокою — «центр масового простору».) Кут\( \theta\) - це кут, через який\( m_{1}\) був розсіяний («кут розсіювання»). Я вказав на малюнку, як це пов'язано з\( \alpha_{1}\) та\( \beta_{1}\) Розділом 5.3. Зверніть увагу, що\( m_{2}\) (спочатку стаціонарні) відколює по лінії центрів.

Наступні два рівняння виражають сталість лінійного імпульсу системи.

\[(m_{1}+m_{2})V = m_{1}u = m_{1}v_{1}\cos\theta + m_{2}v_{2} \cos \alpha_{1}. \tag{5.5.1}\label{eq:5.5.1} \]

Я збираюся намалювати, на малюнку V.4, ситуацію «крупним планом», щоб ви могли бачити геометрію чіткіше. Зверніть увагу, що відстань\( b\) називається параметром удару. Це відстань, на яку два центри пропустили б один одного, якби перша частинка не була розкидана.

На малюнку В.5 малюю ситуацію в центрі масового простору, в якому центр мас\( C\) нерухомий. У цій системі відліку я просто повинен відняти\( \bf{V}\) від усіх швидкостей. Зверніть увагу, що в центрі масового простору швидкості частинок не змінюються при зіткненні. У центрі масового простору,\( m_{1}\) розкидано через кут\( \theta^{\prime}\), і я збираюся знайти зв'язок між\( \theta^{\prime}\),\( \theta\) і коефіцієнтом маси\( \dfrac{m_{2}}{m_{1}}\).

Я почну з глибокого твердження, що

\[\tan \theta = \dfrac{v_{1}\sin\theta}{v_{1}\cos\theta} \tag{5.5.2}\label{eq:5.5.2} \]

Зараз\( v_{1} \sin \theta\) є\( y\) -складовою кінцевої швидкості роботи\( m_{1}\) в лабораторному просторі. \( y\)-складова кінцевої швидкості\( m_{1}\) в центрі масового простору є\( u^{\prime}\sin\theta^{\prime}\), і ці два рівні, так як\( y\) -компонент руху не впливає зміна системи відліку. Тому

\[\tan \theta = \dfrac{u'\sin\theta'}{v_{1}\cos\theta}. \tag{5.5.3}\label{eq:5.5.3} \]

Тому

\[v_{1} \sin \theta = u' \sin \theta'. \tag{5.5.4}\label{eq:5.5.4} \]

\( x\)-компоненти швидкостей «до» і «після»\( m_{1}\) пов'язані

\[v_{1} \cos \theta = u' \sin \theta'+ V. \tag{5.5.6}\label{eq:5.5.6} \]

Замістіть рівняння\( \ref{eq:5.5.4}\) і\( \ref{eq:5.5.6}\) в рівняння\( \ref{eq:5.5.2}\) для отримання

\[\tan \theta = \dfrac{\sin \theta'}{\cos \theta' + V/u'} \tag{5.5.7}\label{eq:5.5.7} \]

Але

\[(m_{1}+m_{2})V = m_{1}u= m_{1}(u'+V), \tag{5.5.8}\label{eq:5.5.8} \]

з якого

\[\dfrac{V}{u'} = \dfrac{m_{1}}{m_{2}}. \tag{5.5.9}\label{eq:5.5.9} \]

Підставивши це в рівняння\( \ref{eq:5.5.7}\), ми отримуємо співвідношення, яке ми шукали:

\[\tan \theta = \dfrac{\sin \theta '}{cos \theta' +m_{1} /m_{2}}. \tag{5.5.10}\label{eq:5.5.10} \]

Це співвідношення проілюстровано на малюнку V.6 для декількох масових співвідношень.

Спробуємо інтерпретувати Малюнок. Для\( m_{2}>m_{1}\), будь-який кут розсіювання, вперед або назад, можливий, але для\( m_{2}<m_{1}\), зворотне розсіювання неможливо, а розсіювання вперед можливо тільки до максимуму. Цього тільки слід очікувати. При цьому для параметра удару нуль або з\( R_{1} + R_{2}\), причому\( m_{2}<m_{1}\), кут розсіювання\( \theta\) повинен дорівнювати нулю, а тому для проміжних параметрів удару він повинен пройти максимум. Це було б зрозуміліше, якби ми могли побудувати кут розсіювання в порівнянні з параметром впливу, і дійсно це те, що ми спробуємо зробити. Тим часом це легко показати, шляхом диференціації Рівняння\( \ref{eq:5.5.10}\) (зроби це!) , що максимальний кут розсіювання дорівнює\( \sin^{-1}\mu\), де

\[ \mu = \dfrac{m_{2}}{m_{1}}. \nonumber \]

Тобто, якщо розсіяна частинка дуже масивна в порівнянні з частинкою, що розсіює, то максимальний кут розсіювання невеликий — тільки слід очікувати.

Зараз я хочу зробити дві речі - одну, обчислити кут розсіювання\( \theta\) як функцію параметра удару, і дві, щоб обчислити\( \dfrac{v_{1}}{u}\) як функцію кута розсіювання. Я збираюся почати з рівнянь 5.4.1, 5.4.2 і 5.4.4, за винятком наступного. Припустимо\( e = 1\) (пружне зіткнення), і\( u_{2}=0\) (\( m_{2}\)спочатку нерухоме), і\( \beta_{2}=0\) (оскільки\( m_{2}\) спочатку нерухоме, воно повинно рухатися по лінії центрів після зіткнення). Так як я хочу спробувати обчислити кут розсіювання, то напишу\( \theta + \alpha_{1}\) для\( \beta_{1}\) (див. Рис. V.4). Я теж буду писати\( r_{1}\),\( r_{2}\) і\( \mu\) для безрозмірних співвідношень\( \dfrac{v_{1}}{u}\),\( \dfrac{v_{2}}{u}\) і\( \dfrac{m_{2}}{m_{1}}\) відповідно. З цими невеликими змінами рівняння 5.4.1, 5.4.2 та 5.4.4 стають

\[r_{1}\cos(\theta + \alpha_{1}) + \mu r_{2} = \cos \alpha_{1}, \tag{5.5.11}\label{eq:5.5.11} \]

\[r_{1}sin(\theta + \alpha_{1})= \sin \alpha_{1}, \tag{5.5.12}\label{eq:5.5.12} \]

\[r_{2} - r_{1}\cos(\theta + \alpha_{1})= \cos \alpha_{1}. \tag{5.5.13}\label{eq:5.5.13} \]

Виключити\( r_{2}\) з рівнянь\( \ref{eq:5.5.11}\) і\( \ref{eq:5.5.13}\) отримати

\[r_{1}\cos(\theta + \alpha_{1})=M \cos \alpha_{1}, \tag{5.5.14}\label{eq:5.5.14} \]

де

\[M = \dfrac{1- \mu}{1+ \mu} = \dfrac{m_{1}-m_{2}}{m_{1}+m_{2}}. \tag{5.5.15}\label{eq:5.5.15} \]

Якщо ми тепер виключити\( \alpha_{1}\) з Рівняння\( \ref{eq:5.5.12}\) і\( \ref{eq:5.5.14}\), ми отримаємо співвідношення між\( \dfrac{v_{1}}{u}\) і кутом розсіювання, який був другою з наших двох цілей вище. Усунення легко робиться наступним чином. Розгорніть\ sin і cos\( \theta + \alpha_{1}\) у двох рівняннях, розділіть обидві сторони кожного рівняння на\( \cos \alpha_{1}\) і усуньте\( \tan\alpha_{1}\) між двома рівняннями. Результат -

\[r^{2}_{1} (1+M)\cos\theta +M = 0. \tag{5.5.16}\label{eq:5.5.16} \]

Ми подивимося на це рівняння в мить, але тим часом, замість того, щоб виключити\( \alpha_{1}\) з Рівняння\( \ref{eq:5.5.12}\) і\( \ref{eq:5.5.14}\), давайте усунути\( r_{1}\). Це дасть нам зв'язок між кутом розсіювання\( \theta\) і\( \alpha_{1}\), і, оскільки він тісно\( \alpha_{1}\) пов'язаний з параметром впливу (див. Рис. V.4), це дозволить досягти першої з наших цілей, а саме знайти кут розсіювання як функцію параметра впливу. Якщо ви робите алгебру, ви повинні виявити, що відношення між\( \theta\) і\( \alpha_{1}\) є

\[t = \dfrac{a(1-M)}{a^{2}+M}, \tag{5.5.17}\label{eq:5.5.17} \]

де

\[t = \\tan \theta \quad and \quad a = \\tan \alpha_{1}. \tag{5.5.17a,b}\label{eq:5.5.17a,b} \]

Тепер нехай

\[b' = \dfrac{b}{R_{1}+R_{2}} \tag{5.5.18}\label{eq:5.5.18} \]

і з малюнка V.5 ми бачимо, що

\[b' = \sin \alpha_{1}. \tag{5.5.19}\label{eq:5.5.19} \]

При виключенні\( \alpha_{1}\) з\( \ref{eq:5.5.19}\) рівнянь\( \ref{eq:5.5.17}\) і отримано необхідне співвідношення між кутом розсіювання\( \theta\) і (безрозмірним) параметром удару\( b'\):

\[\tan \theta = \dfrac{s\mu b' \sqrt{1-b^{t^{2}}}}{1- \mu + 2 \mu b^{t^{2}}}. \tag{5.5.20}\label{eq:5.5.20} \]

Це співвідношення показано на малюнку V .7. Значення коефіцієнта маси\( \mu\) (\(=frac{m_{2}}{m_{1}}\)) є (від

найнижчий вгору)\( \dfrac{1}{8} , \dfrac{1}{4}, \dfrac{1}{2}, \dfrac{9}{10}, 1 , \dfrac{10}{9}, 2, 4, 8\) і (пунктирним)\( \infty\). Цей малюнок, мабуть, трохи легше інтерпретувати, ніж малюнок V.6. Можна помітити, що для\( \mu > 1\), будь-який кут розсіювання можливий\( \mu < 1\), але для, кут розсіювання має максимально можливе значення, менше 90 °, а кут розсіювання дорівнює нулю для\( b'\) = 0 або 1.

Вправа\(\PageIndex{1}\)

Ми побачили, шляхом диференціювання рівняння\( \ref{eq:5.5.10}\), що максимальний кут розсіювання був\( \sin^{-1}\mu\). Тепер покажіть те ж саме шляхом диференціації рівняння\( \ref{eq:5.5.20}\). (Це не так просто, чи не так?)

Показати, що кут розсіювання є найбільшим для параметра удару

\[b' = \sqrt{\dfrac{1 - \mu}{2}}. \tag{5.5.21}\label{eq:5.5.21} \]

Рішення

Ви помітите, що для/(b' = 0/) (лобове зіткнення) кут розсіювання різко змінюється від 0 до 180 °, оскільки співвідношення маси змінюється від менш ніж 1 до більш ніж 1. Там немає проблем. Але якщо коефіцієнт маси рівно 1 (не самий крихітний трохи менше або самий крихітний трохи більше), кут розсіювання, мабуть, 90 °. Це може викликати деяке здивування, поки не зрозуміється, що для лобового\( \mu = 1\) зіткнення з першою сферою приходить в глухий кут.

Випадок\( mu = \infty\) (друга сфера нерухома) представляє певний інтерес. У цьому випадку легко обчислити, як кут розсіювання змінюється залежно від параметра удару для пружного зіткнення, лише вимагаючи, щоб розсіяна сфера підкорялася закону відбиття, і без будь-якого посилання на рівняння\( \ref{eq:5.5.20}\).

Вправа\(\PageIndex{2}\)

Легка вправа.

Без будь-якого посилання на рівняння\( \ref{eq:5.5.20}\), показати, що, якщо друга куля нерухома, кут розсіювання пов'язаний з параметром удару

\[\theta = 180° - 2sin^{-1} b'. \tag{5.5.22}\label{eq:5.5.22} \]

Не так-то легка вправа. Показати, що в межі як\( \mu\rightarrow\infty\), Рівняння\( \ref{eq:5.5.20}\) наближається до Рівняння\( \ref{eq:5.5.22}\).

У будь-якому випадку граничний випадок, коли друга сфера стає нерухомою, показаний у вигляді пунктирної кривої на малюнку V.7.

Вправа середньої складності. Коефіцієнт маси\( \dfrac{m_{2}}{m_{1}}\) дорівнює 0,9, а кут розсіювання - 50\(^{\circ}\). Яким був параметр впливу?

Відповіді

b' = 0,07270 або 0,58540.

Зараз ми розглянули напрямок руху\( m_{1}\) після розсіювання як функції параметра удару. Тепер ми повинні подивитися на швидкість\( m_{1}\) після зіткнення, і це повертає нас до Рівняння\( \ref{eq:5.5.16}\), яке дає швидкість (\( r_{1}=\dfrac{v_{1}}{u}\)) як функцію кута розсіювання\( \theta\). Він дорівнює 11 квадратичним дюймам\( r_{1}\), отже, для заданого кута розсіювання є дві можливі швидкості - що не дивно, адже заданий кут розсіювання може виникнути з двох різних параметрів удару, як ми щойно з'ясували. Ми можемо зручно показати співвідношення між\( r_{1}\) і\( \theta\) просто шляхом побудови рівняння в полярних координатах. Я перепишу рівняння тут для зручності довідки:

\[r^{2}_{1} = r_{1}(1+M)\cos\theta + M = 0. \tag{5.5.16.}\label{eq:5.5.16.} \]

Ось\( M = \dfrac{1-\mu}{1+ \mu }=\dfrac{1}{1+ \mu } \), але я хочу написати рівняння через масові частки

\[q_{1} = \dfrac{m_{1}}{m_{1}+m_{2}} = \dfrac{1}{1 + \mu} \quad and \quad q_{2} = \dfrac{m_{2}}{m_{1}+m_{2}}=\dfrac{\mu}{1 + \mu}. \tag{5.5.23a,b}\label{eq:5.5.23a,b} \]

Якщо ви працюєте над цим протягом короткого часу, ви виявите, що Рівняння\( \ref{eq:5.5.16}\) стає

\[r_{1}^{2} +q_{1}^{2} -2r_{1}q_{1}\cos\theta = q_{2}^{2}. \tag{5.5.24}\label{eq:5.5.24} \]

і один потім долається з непереборним бажанням намалювати трикутник:

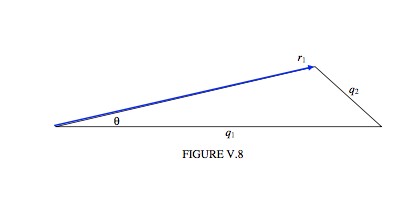
Для заданого співвідношення маси локус\( r_{1}\) (швидкість) проти\( \theta\) (кут розсіювання) є таким, що\( q_{1}\) і\( q_{2}\) є постійними — іншими словами, це коло:

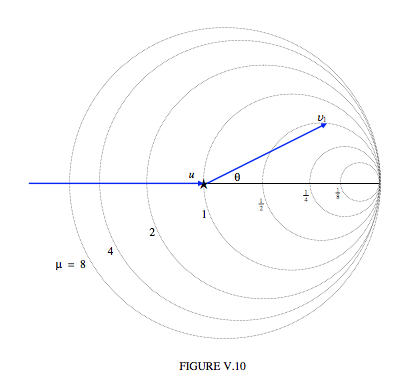
Можна уявити, що перша частинка надходить зліва зі швидкістю u і зіткнення відбувається у зірочки, а після зіткнення вона рухається зі швидкістю\( r_{1}\) рази\( u\) в напрямку\( \theta\), величина її вектора швидкості визначається тим, де вектор перетинає коло (у двох можливих місцях), задане рівнянням\( \ref{eq:5.5.24}\). Максимальний кут розсіювання відповідає вектору швидкості, який є дотичним до кола. Якщо зірочка є полюсом (початком) полярних координат, центр кола знаходиться на відстані\( q_{1}\) від полюса, а його радіус дорівнює\( q_{2}\). На малюнку В.10 показані кола, відповідні кільком масовим співвідношенням. Малюнок графічно ілюструє зв'язок між\( u\)\( v_{1}\),\( \theta\) і\( \mu\). Ви можете бачити, наприклад, що якщо\( \mu>1\), розсіювання через будь-який кут можливо, і співвідношення між\( v_{1}\) і\( \theta\) є унікальним; але якщо\( \mu<1\), можливо тільки пряме розсіювання, до максимуму\( \theta\), і, для заданого\( \theta\), є два рішення для \( v_{1}\).

Це стосується того, що відбувається зі сферою\( m_{1}\). Тепер ми можемо звернути свою увагу на\( m_{2}\). Починаючи з рівнянь\( \ref{eq:5.5.11}\)\( \ref{eq:5.5.13}\),\( \ref{eq:5.5.12}\) і, ми хочемо усунути\( r_{1}\) і\( \theta\) - дійсно все, що стосується сфери\( m_{1}\).

Якщо ви звернетеся до рисунку V.4, ви побачите,\( m_{2}\) що після зіткнення відступає під кутом\( \alpha_{1}\) до початкового напрямку руху\( m_{1}\). Тому я думаю, що цікаво знайти зв'язок між \( r_{2}\)(\ dfrac {v_ {2}} {u}) і\( \alpha_{1}\). Якщо нам вдасться це зробити, це означає, що ми також можемо знайти зв'язок, якщо хочемо, між\( r_{2}\) параметром впливу, оскільки\( b' = \sin\alpha_{1}\). Це легко усунути\( r_{1}\) з Рівняння\( \ref{eq:5.5.12}\) і\(\ref{eq:5.5.13}\), і тоді ви можете отримати\( \tan(\theta + \alpha_{1})\) від Рівняння\( \ref{eq:5.5.14}\), і, отже, отримати необхідне співвідношення:

\[r_{2} = \dfrac{2\cos\alpha_{1}}{1 + \mu}. \tag{5.5.25}\label{eq:5.5.25} \]

Я намалюю це відношення як полярний графік, \( r_{2}\)проти\( \alpha_{1}\), на малюнку V.11. Я залишу читача, щоб розробити і намалювати відносини між\( r_{2}\) і,\( b'\) якщо він або вона бажає. Рівняння V.11 - полярне рівняння до кола радіуса\( \dfrac{1}{1+\mu}\).

Приклад\(\PageIndex{1}\)

Припустимо, відношення маси\( \mu=\dfrac{m_{2}}{m_{1}} = 0.5\) і кут розсіювання дорівнює\( \theta=\) 20 °. Рівняння\( \ref{eq:5.5.16}\) або малюнок V.10 покаже, що\( r_{1}\) = 0,8696 або 0,3833. Рівняння\( \ref{eq:5.5.17}\) покаже, що\( \alpha_{1}\) = 58 ° .4 або 11 ° .6. І рівняння\( \ref{eq:5.5.25}\) або малюнок V.11 покаже, що\( r_{2}\) = 0,6983 або 1,306. Я залишу це читачеві, щоб визначити, які альтернативні значення\( r_{1}\),\( r_{2}\) і\( \alpha_{1}\) йти разом.