3.2: Момент сили

Last updated
Save as PDF

Page ID: 76329

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Для початку розглянемо звичну двомірну ситуацію. На малюнку III.1 малюю силу\(\textbf{F}\) і точку О. Момент сили щодо О можна визначити як

Сила разів перпендикулярна відстань від O до лінії дії\(\textbf{F}\).

альт

Крім того, (рис. III.2) момент можна визначити однаково добре

Поперечна складова сили часу відстані від О до точки прикладання сили.

альт

Так чи інакше, величина моменту сили, також відома як крутний момент, є\(rF \sin\theta\) Ми можемо розглядати його як вектор\( \boldsymbol\tau \), перпендикулярний площині паперу:

\ почати {рівняння}\\ напівжирний символ\ тау =\ textbf {r}\ times\ textbf {F}\ тег {3.2.1}\ мітка {eq:3.2.1}\ кінець {рівняння}

Тепер дозвольте мені поставити запитання. Чи правильно говорити момент сили щодо (або «про») точку або щодо (або «про») осі?

У наведеному вище двовимірному прикладі це не має значення, але тепер дозвольте перейти до трьох вимірів, і я постараюся уточнити.

На малюнку III.3 малюю набір прямокутних осей\(\textbf{F}\), і силу, вектор положення якої щодо початку є\(\textbf{r}\).

альт

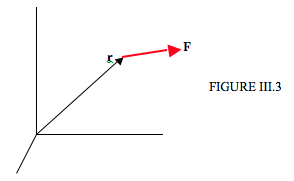
Момент, або крутний момент, щодо походження є вектором\(\textbf{F}\)

\ почати {рівняння}\\ напівжирний символ\ тау =\ textbf {r}\ times\ textbf {F}\ тег {3.2.2}\ мітка {eq:3.2.2}\ кінець {рівняння}

\( x-, y-\)А\( z\) - складовими\( \boldsymbol\tau \) є моменти\(\textbf{F}\) стосовно\(x-, y-\) і z-осей. Ви можете легко знайти компоненти,\( \boldsymbol\tau \) розширивши крос-продукт\( \ref{eq:3.2.2}\):

\[ \boldsymbol\tau = \hat{\textbf{x}}(yF_{z}-zF_{y})+\hat{\textbf{y}}(yF_{x}-xF_{z})+\hat{\textbf{z}}(xF_{y}-yF_{x}) \tag{3.2.3}\label{eq:3.2.3} \]

де\( \bf \hat{x},\hat{y},\hat{z}\) - одиничні вектори по\( x,y,z\) осях. На малюнку III.4, ми дивимося вниз\( x\) -вісь, і я намалював компоненти\( F_{y}\) і\( F_{z}\), і ви можете бачити, що, дійсно,\( \tau_{x} =yF_{z}-zF_{y}\).

альт

Розміри моменту сили, або крутного моменту, складають ML ² T ^{- 2}, а одиниці СІ - N м. (Найкраще залишити одиниці як N м, а не виражати крутний момент в джоулі.)