1.6: Теореми Паппуса

(Паппус Александрін, грецький математик, приблизно 3 або 4 століття нашої ери.)

1. Якщо плоска область обертається навколо осі в її площині, але яка не перетинає площу, об'єм змітається дорівнює площі, що помножується на відстань, переміщену центроїдом.
2. Якщо плоска крива обертається навколо осі в її площині, але яка не перетинає криву, площа зміщеної дорівнює довжині відстані, переміщеної центроїдом.

Ці теореми дозволяють нам виробити об'єм твердого тіла обертання, якщо ми знаємо положення центроїда плоської області, або навпаки; або опрацювати площу поверхні обертання, якщо ми знаємо положення центроїда плоска крива або навпаки. Не обов'язково, щоб площину або криву поверталися через повні 360 ^о.

Спочатку доведемо теореми. Потім ми слідуємо з деякими прикладами.

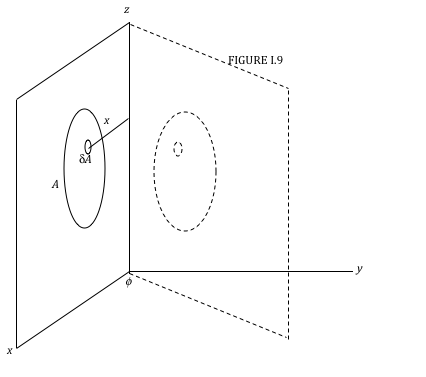
Розглянемо площу\( A \) в\( zx \) площині (рис. I.9), і елемент\( \delta A \) в межах області на відстані\( x \) від\( z \) осі. Поверніть ділянку на кут\( \phi \) навколо\( z \) осі. Довжина дуги, що простежується елементом\( dA \) при переміщенні через кут\( x \phi \),\( \phi \) є, тому обсяг змітається\( \delta A \) є\( x \phi \delta A \). Обсяг, змітається на всю площу, є\( \phi \)\(\int xd A\). Але визначення центроїда\( A \) таке, що його відстань від\( z \) осі задається\( \overline{x} A \) =\(\int x d A\). Тому обсяг змітається площею є\( \phi \overline{x} A \). Але\( \phi \overline{x} \) це відстань, переміщена центроїдом, тому перша теорема Паппуса доведена.

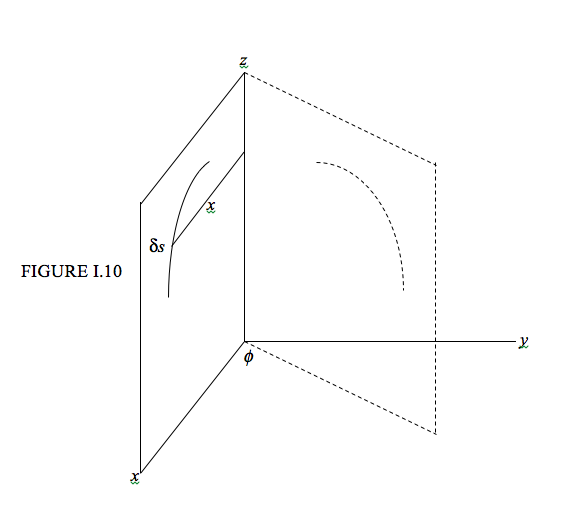
Розглянемо криву довжини\(L\) in the \( zx \) plane (Figure I.10), and an element \( \delta s \) of the curve at a distance \( x \) from the \( z \) axis. Rotate the curve through an angle \( \phi \) про\( z \) axis. The length of the arc traced by the element \( \delta s \)in moving through an angle \( \phi \) є\( x\phi \), так що область\( \delta s \) змітається\( x \phi \delta s \) . Площа, вимітається всією кривою, є\( \phi \int x ds \). Але визначення центроїда таке, що його віддаленість від\( z \) axis is given by \( \overline{x}L = \int xds \). Тому область, вимітається кривою, є\( \phi \overline{x} L \). Але\( \phi \overline{x} \) чи переміщається відстань центроїдом, тому доведена друга теорема Паппуса.

Застосування теорем Паппуса

Поверніть площину напівкруглої фігури площею\( \frac{1}{2} \pi a^{2} \) через 360 ^o про її діаметр. Обсяг змітається є\( \frac{4}{3} \pi a^{3} \) , а відстань, яку переміщає центроїд,\( 2 \pi \overline{x} \) тому теоремою Паппуса,\( \overline{x} = \frac{4a}{(3 \pi )} \).

Поверніть площину напівкруглої дуги довжиною π a через 360 ^o про її діаметр. Скористайтеся подібним аргументом, щоб показати, що\( \overline{x} = \frac{2a} { \pi} \).

Розглянемо прямокутний трикутник, висоту\( h \), base \( a \) (Figure I.11). Its centroid is at a distance \( \frac{a}{3} \) from the height \( h \). The area of the triangle is \( \frac{ah}{2} \). Rotate the triangle through 360^o about \( h \). The distance moved by the centroid is \( \frac{2 \pi a}{3} \). The volume of the cone swept out is \( \frac{ah}{2} \) times \( \frac{2 \pi}{3} \), equals \( \frac{ \pi a^{2} h}{3} \) .

Тепер розглянемо лінію довжини,\( l\) inclined at an angle \( \alpha\) щоб площа поверхні конуса зміталася\( l \times\pi\ l \sin \alpha =\pi l^{2} \sin \alpha \).\( y \) axis (Figure I.12). Its centroid is at a distance \( \frac{1}{2} l \sin \alpha \) from the \( y \) axis. Rotate the line through 360^o about the \( y \) axis. The distance moved by the centroid is \( 2 \pi \times \frac{1}{2} l \sin \alpha = \pi l \sin \alpha \).

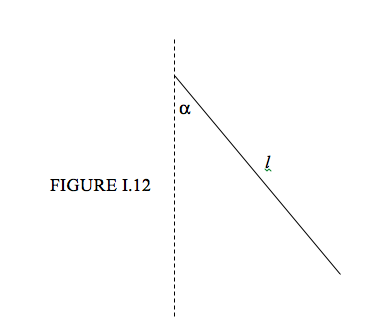
Центр кола радіусом\( b \) is at a distance \( a \) from the \( y \) axis. It is rotated through 360^o about the \( y \) axis to form a torus (Figure I.13). Use the theorems of Pappus to show that the volume and surface area of the torus are, respectively, \( 2 \pi ^{2} ab^{2} \) і\( 4 \pi ^{2} ab\).