23.6: Примусове затухання осцилятора

Проведемо нашу затухлу систему пружинних об'єктів синусоїдальною силою. Припустимо, що х - складова рушійної сили задається

$$F_{x}(t)=F_{0} \cos (\omega t) \nonumber$$

де$F_{0}$ називається амплітудою (максимальним значенням) і$\omega$ є рушійною кутовою частотою. Сила змінюється між$F_{0}$ і$-F_{0}$ тому, що функція косинуса коливається між +1 і −1. Визначте x (t) як положення об'єкта щодо положення рівноваги. Х -складова сили, що діє на об'єкт, тепер є сумою

$$F_{x}=F_{0} \cos (\omega t)-k x-b \frac{d x}{d t} \nonumber$$

Другий закон Ньютона в х -напрямку стає

$$F_{0} \cos (\omega t)-k x-b \frac{d x}{d t}=m \frac{d^{2} x}{d t^{2}} \nonumber$$

Ми можемо переписати рівняння (23.6.3) як

$$F_{0} \cos (\omega t)=m \frac{d^{2} x}{d t^{2}}+b \frac{d x}{d t}+k x \nonumber$$

Виведено розв'язок рівняння (23.6.4) у додатку 23Е: Розв'язок вимушеного рівняння осцилятора. Рішення задається функцією

$$x(t)=x_{0} \cos (\omega t+\phi) \nonumber$$

де амплітуда$x_{0}$ є функцією ведучої кутової частоти ω і задається

$$x_{0}(\omega)=\frac{F_{0} / m}{\left((b / m)^{2} \omega^{2}+\left(\omega_{0}^{2}-\omega^{2}\right)^{2}\right)^{1 / 2}} \nonumber$$

Фазова постійна φ також є функцією ведучої кутової частоти ω і задається

$$\phi(\omega)=\tan ^{-1}\left(\frac{(b / m) \omega}{\omega^{2}-\omega_{0}^{2}}\right) \nonumber$$

У рівняннях (23.6.6) та (23.6.7)

$$\omega_{0}=\sqrt{\frac{k}{m}} \nonumber$$

- це природна кутова частота, пов'язана з некерованим осцилятором без затухання. x -складову швидкості можна знайти шляхом диференціювання рівняння (23.6.5),

$$v_{x}(t)=\frac{d x}{d t}(t)=-\omega x_{0} \sin (\omega t+\phi) \nonumber$$

де амплітуда$x_{0}(\omega)$ задається рівнянням (23.6.6), а фазова постійна$\phi(\omega)$ - рівнянням (23.6.7).

Резонанс

Коли$b / m<<2 \omega_{0}$ ми говоримо, що осцилятор злегка затухає. Для злегка затухаючого керованого генератора після перехідного періоду положення об'єкта буде коливатися з тією ж кутовою частотою, що і рушійна сила. Графік амплітуди$x_{0}(\omega)$ проти ведучої кутової частоти ω для злегка затухаючого примусового генератора показаний на малюнку 23.16. Якщо кутова частота збільшена з нуля, амплітуда$x_{0}(\omega)$ буде збільшуватися до тих пір, поки вона не досягне максимуму, коли кутова частота рушійної сили буде такою ж, як і власна кутова частота,$\omega_{0}$ пов'язана з негаслим осцилятором. Це називається резонансом. При збільшенні рушійної кутової частоти вище власної кутової частоти амплітуда коливань положення зменшується.

Малюнок 23.16 Ділянка амплітуди$x_{0}(\omega)$ проти водіння кутової частоти ω для злегка затухаючого генератора з$b / m<<2 \omega_{0}$

Ми можемо знайти кутову частоту таку, що амплітуда$x_{0}(\omega)$ знаходиться на максимумі, встановивши похідну Рівняння (23.6.6) рівну нулю,

$$0=\frac{d}{d t} x_{0}(\omega)=-\frac{F_{0}(2 \omega)}{2 m} \frac{\left((b / m)^{2}-2\left(\omega_{0}^{2}-\omega^{2}\right)\right)}{\left((b / m)^{2} \omega^{2}+\left(\omega_{0}^{2}-\omega^{2}\right)^{2}\right)^{3 / 2}} \nonumber$$

Це зникає, коли

$$\omega=\left(\omega_{0}^{2}-(b / m)^{2} / 2\right)^{1 / 2} \nonumber$$

Для слабозатухаючого осцилятора$\omega_{0}>>(1 / 2) b / m$, і тому максимальне значення амплітуди відбувається, коли

$$\omega \simeq \omega_{0}=(k / m)^{1 / 2} \nonumber$$

Амплітуда при резонансі тоді

$$x_{0}\left(\omega=\omega_{0}\right)=\frac{F_{0}}{b \omega_{0}} \quad \text { (lightly damped) } \nonumber$$

Графік фазової постійної$\phi(\omega)$ проти ведучої кутової частоти ω для злегка затухаючого примусового генератора показаний на малюнку 23.17.

Малюнок 23.17 Ділянка фазової постійної$\phi(\omega)$ проти водіння кутової частоти ω для злегка затухаючого генератора з$b / m<<2 \omega_{0}$

Стала фази при резонансі дорівнює нулю,

$$\phi\left(\omega=\omega_{0}\right)=0 \nonumber$$

При резонансі х -складова швидкості задається

$$v_{x}(t)=\frac{d x}{d t}(t)=-\frac{F_{0}}{b} \sin \left(\omega_{0} t\right) \quad \text { (lightly damped) } \nonumber$$

Коли генератор не злегка затухає$\left(b / m \simeq \omega_{0}\right)$, резонансний пік зміщується вліво,$\omega=\omega_{0}$ як показано на графіку амплітуди проти кутової частоти на малюнку 23.18. Відповідний графік фазової постійної проти кутової частоти для незлегка затухаючого генератора показаний на малюнку 23.19.

Малюнок 23.18 Ділянка амплітуди проти кутової частоти для слабозатухаючого керованого генератора, де$b / m \simeq \omega_{0}$

Малюнок 23.19 Ділянка фазової постійної проти кутової частоти для слабозатухаючого керованого генератора, де$b / m \simeq \omega_{0}$

Механічна енергія

Кінетична енергія для керованого затухаючого осцилятора задається

$$K(t)=\frac{1}{2} m v^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi) \nonumber$$

Потенційна енергія дається

$$U(t)=\frac{1}{2} k x^{2}(t)=\frac{1}{2} k x_{0}^{2} \cos ^{2}(\omega t+\phi) \nonumber$$

Механічна енергія тоді

$$E(t)=\frac{1}{2} m v^{2}(t)+\frac{1}{2} k x^{2}(t)=\frac{1}{2} m \omega^{2} x_{0}^{2} \sin ^{2}(\omega t+\phi)+\frac{1}{2} k x_{0}^{2} \cos ^{2}(\omega t+\phi) \nonumber$$

Приклад 23.5: Механічна енергія, усереднена за часом

Період одного циклу задається по$T=2 \pi / \omega$. Покажіть, що

(i)$\frac{1}{T} \int_{0}^{T} \sin ^{2}(\omega t+\phi) d t=\frac{1}{2}$

(ii)$\frac{1}{T} \int_{0}^{T} \cos ^{2}(\omega t+\phi) d t=\frac{1}{2}$

(iii)$\frac{1}{T} \int_{0}^{T} \sin (\omega t) \cos (\omega t) d t=0$

Рішення: (i) Використовуємо тригонометричну ідентичність

$$\left.\sin ^{2}(\omega t+\phi)\right)=\frac{1}{2}(1-\cos (2(\omega t+\phi)) \nonumber$$

переписати інтеграл у рівнянні (23.6.19) як

$$\left.\frac{1}{T} \int_{0}^{T} \sin ^{2}(\omega t+\phi)\right) d t=\frac{1}{2 T} \int_{0}^{T}(1-\cos (2(\omega t+\phi)) d t \nonumber$$

Інтеграція прибутковості

\ [\ begin {масив} {l}
\ frac {1} {2 T}\ int_ {0} ^ {T}\ лівий (1-\ cos (2 (\ омега т+\ фі)) d t=\ frac {1} {2} -\ лівий. \ ліворуч (\ frac {\ sin (2 (\ омега т+\ фі))} {2\ омега}\ праворуч)\ праворуч | _ {T = 0} ^ {T = 2\ pi/\ омега}\ праворуч. \\
=\ гідророзриву {1} {2} -\ лівий (\ frac {\ sin (4\ pi+2\ phi)} {2\ омега} -\ frac {\ sin (2\ phi)} {2\ омега}\ право) =\ frac {1} {2}
\ кінець {масив}\ nonumber\]

де ми використовували тригонометричну ідентичність, яка

$$\sin (4 \pi+2 \phi)=\sin (4 \pi) \cos (2 \phi)+\sin (2 \phi) \cos (4 \pi)=\sin (2 \phi) \nonumber$$

Доведення рівняння (23.6.19).

(ii) Ми використовуємо подібний аргумент, що починається з тригонометричної ідентичності, яка

$$\left.\cos ^{2}(\omega t+\phi)\right)=\frac{1}{2}(1+\cos (2(\omega t+\phi)) \nonumber$$

Тоді

$$\left.\frac{1}{T} \int_{0}^{T} \cos ^{2}(\omega t+\phi)\right) d t=\frac{1}{2 T} \int_{0}^{T}(1+\cos (2(\omega t+\phi)) d t \nonumber$$

Інтеграція прибутковості

\ [\ begin {масив} {l}
\ frac {1} {2 T}\ int_ {0} ^ {T}\ лівий (1+\ cos (2 (\ омега т+\ фі)) d t=\ frac {1} {2} +\ ліворуч. \ ліворуч (\ frac {\ sin (2 (\ омега т+\ фі))} {2\ омега}\ праворуч)\ праворуч | _ {T = 0} ^ {T = 2\ pi/\ омега}\ праворуч. \\
=\ гідророзриву {1} {2} +\ лівий (\ frac {\ sin (4\ pi+2\ phi)} {2\ омега} -\ frac {\ sin (2\ phi)} {2\ омега}\ право) =\ frac {1} {2}
\ кінець {масив}\ nonumber\]

(iii) Спочатку ми використовуємо тригонометричну ідентичність, яка

$$\sin (\omega t) \cos (\omega t)=\frac{1}{2} \sin (\omega t) \nonumber$$

Тоді

\ [\ почати {масив} {l}
\ frac {1} {T}\ int_ {0} ^ {T}\ sin (\ омега т)\ cos (\ омега т) d t=\ frac {1} {T}\ int_ {0} ^ {T}\ sin (\ омега т) д т\\
=-\ ліворуч. \ frac {1} {T}\ frac {\ cos (\ омега т)} {2\ омега}\ right|_ {0} ^ {T} =-\ frac {1} {2\ омега T} (1-1) =0
\ кінець {масив}\ nonumber\]

Значення інтегралів у прикладі 23.5 називаються усередненими за часом значеннями. Позначимо середньочасове значення функції f (t) за один період

$$\langle f\rangle \equiv \frac{1}{T} \int_{0}^{T} f(t) d t \nonumber$$

Зокрема, середньочасова кінетична енергія як функція кутової частоти задається

$$\langle K(\omega)\rangle=\frac{1}{4} m \omega^{2} x_{0}^{2} \nonumber$$

Усереднена за часом потенційна енергія як функція кутової частоти задається

$$\langle U(\omega)\rangle=\frac{1}{4} k x_{0}^{2} \nonumber$$

Усереднене за часом значення механічної енергії як функції кутової частоти задається

$$\langle E(\omega)\rangle=\frac{1}{4} m \omega^{2} x_{0}^{2}+\frac{1}{4} k x_{0}^{2}=\frac{1}{4}\left(m \omega^{2}+k\right) x_{0}^{2} \nonumber$$

Тепер ми замінюємо рівняння (23.6.6) для амплітуди в рівняння (23.6.34), що дає

$$\langle E(\omega)\rangle=\frac{F_{0}^{2}}{4 m} \frac{\left(\omega_{0}^{2}+\omega^{2}\right)}{\left((b / m)^{2} \omega^{2}+\left(\omega_{0}^{2}-\omega^{2}\right)^{2}\right)} \nonumber$$

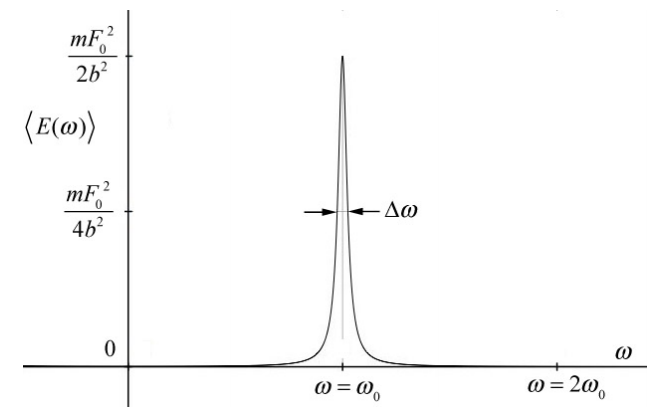
Графік усередненої за часом енергії проти кутової частоти для слабозатухаючого випадку$\left(b / m<<2 \omega_{0}\right)$ показаний на малюнку 23.20.

Малюнок 23.20). Спочатку ми підставляємо$\omega=\omega_{0}$ всюди в Рівняння (23.6.35), крім терміну,$\omega_{0}^{2}-\omega^{2}$ який з'являється в знаменнику, що дає

$$\langle E(\omega)\rangle=\frac{F_{0}^{2}}{2 m} \frac{\left(\omega_{0}^{2}\right)}{\left((b / m)^{2} \omega_{0}^{2}+\left(\omega_{0}^{2}-\omega^{2}\right)^{2}\right)} \nonumber$$

Ми можемо наблизити термін

$$\omega_{0}^{2}-\omega^{2}=\left(\omega_{0}-\omega\right)\left(\omega_{0}+\omega\right) \simeq 2 \omega_{0}\left(\omega_{0}-\omega\right) \nonumber$$

Тоді рівняння (23.6.36) стає

$$\langle E(\omega)\rangle=\frac{F_{0}^{2}}{2 m} \frac{1}{\left((b / m)^{2}+4\left(\omega_{0}-\omega\right)^{2}\right)} \quad \text { (lightly damped) } \nonumber$$

Правий вираз Рівняння (23.6.38) набуває свого максимального значення, коли знаменник має мінімальне значення. При огляді це відбувається при$\omega=\omega_{0}$. Як варіант, щоб знайти максимальне значення, ставимо похідну Рівняння (23.6.35) рівну нулю і вирішимо для ω,

\ [\ begin {масив} {l}
0=\ frac {d} {d\ омега}\ ланголь Е (\ омега)\ діапазон =\ frac {d} {d\ омега}\ frac {F_ {0}} {2 м}\ frac {1} {\ лівий (b/m) ^ {2} +4\ лівий (\ omega_ {0} -\ омега\ праворуч) ^ {2}\ праворуч)}\\
=\ розриву {4 F_ {0} ^ {2}} {m}\ frac {\ ліворуч (\ омега_ {0} -\ омега\ праворуч)} {\ ліворуч (b/м) ^ {2} +4\ ліворуч (\ omega_ {0} -\ омега\ праворуч) ^ {2}\ право) ^ {2}}
\ end {масив}\ nonumber\]

Максимум виникає, коли відбувається при$\omega=\omega_{0}$ і має значення

$$\left\langle E\left(\omega_{0}\right)\right\rangle=\frac{m F_{0}^{2}}{2 b^{2}} \quad(\text { underdamped }) \nonumber$$

Усереднена за часом потужність

Усереднена за часом потужність, що подається рушійною силою, задається виразом

$$\langle P(\omega)\rangle=\frac{1}{T} \int_{0}^{T} F_{x} v_{x} d t=-\frac{1}{T} \int_{0}^{T} \frac{F_{0}^{2} \omega \cos (\omega t) \sin (\omega t+\phi)}{m\left((b / m)^{2} \omega^{2}+\left(\omega_{0}^{2}-\omega^{2}\right)^{2}\right)^{1 / 2}} d t \nonumber$$

де ми використовували Рівняння (23.6.1) для рушійної сили, і Рівняння (23.6.9) для x -складової швидкості об'єкта. Використовуємо тригонометричну ідентичність

$$\sin (\omega t+\phi)=\sin (\omega t) \cos (\phi)+\cos (\omega t) \sin (\phi) \nonumber$$

переписати інтеграл у Рівнянні (23.6.41) як два інтеграли

\ [\ begin {масив} {l}
\ лангле P (\ омега)\ rangle=-\ frac {1} {T}\ int_ {0} ^ {T}\ frac {F_ {0} ^ {2}\ омега\ cos (\ омега т)\ sin (\ омега т)\ cos (\ phi)} {м\ ліворуч (b/м) ^ {2}\ omex ga^ {2} +\ лівий (\ омега_ {0} ^ {2} -\ омега^ {2}\ праворуч) ^ {2}\ праворуч) ^ {1/2}} d t\\
-\ frac {1} {T}\ int_ {0} ^ {T}\ frac {F_ {0} ^ {2}\ омега\ cos ^ {2} (\ омега т)\ sin (\ phi)} {м\ ліворуч ((b/м) ^ {2}\ омега^ {2} +\ ліворуч (\ омега_ {0} ^ {2}\ праворуч) ^ {2}\ праворуч) ^ {1/2}}} d t
\ кінець {масив}\ nonumber\]

Використовуючи усереднені за часом результати з Прикладу 23.5, ми бачимо, що перший член у Рівнянні (23.6.43) дорівнює нулю, а другий член стає

$$\langle P(\omega)\rangle=\frac{F_{0}^{2} \omega \sin (\phi)}{2 m\left((b / m)^{2} \omega^{2}+\left(\omega_{0}^{2}-\omega^{2}\right)^{2}\right)^{1 / 2}} \nonumber$$

Для низькозатухаючого керованого осцилятора ми робимо ті самі наближення в Рівнянні (23.6.44), які ми зробили для усередненої за часом енергії. У члені в чисельнику і

член зліва в знаменнику, ми ставимо$\omega=\omega_{0}$, і використовуємо Рівняння (23.6.37) в члені справа в знаменнику, що дає

\ [\ лангове P (\ омега)\ rangle=\ frac {F_ {0} ^ {2}\ sin (\ phi)} {2 м\ ліворуч (b/м) ^ {2} +2\ ліворуч (\ омега_ {0} -\ омега\ праворуч) ^ {1/2}}} (недопалений)\ кінець {рівняння}

Усереднена за часом потужність, розсіюється резистивною силою, задається

\ [\ почати {масив} {l}
\ лівий\ ланкуль P_ {\ mathrm {dis}} (\ омега)\ праворуч\ діапазон =\ frac {1} {T}\ int_ {0} ^ {T}\ ліворуч (F_ {x}\ праворуч) _ {\ mathrm {dis}} v_ {x} d t=\ frac {1} {T}\ int_ {0} ^ {T} b v_ {x} ^ {2} d t=\ frac {1} {T}\ int_ {0} ^ {T}\ frac {F_ {0} ^ {2}\ омега^ {2}\ sin ^ {2} (\ омега т+\ фі) д т} {м^ {2}\ ліво (б/м) {2}\ омега^ {2} +\ ліворуч (\ омега_ {0} ^ {2} -\ омега^ {2}\ праворуч) ^ {2}\ праворуч)}\\
=\ розрив {F_ {0} ^ {2}\ омега^ {2} d t} {2}\ ліворуч ((b/м) ^ {2}\ омега^ {2} +\ омега_ {0} ^ {2} -\ омега^ {2}\ право) ^ {2}\ право)}
\ кінець {масив}\ nonumber\]

де ми використовували Рівняння (23.5.1) для дисипативної сили, Рівняння (23.6.9) для x -складової швидкості об'єкта та Рівняння (23.6.19) для усереднення часу.

Фактор якості

Графік усередненої за часом енергії проти рушійної кутової частоти для недозатухаючого оскальлятора має ширину,$\Delta \omega$ (рис. 23.20). Одним із способів охарактеризувати цю ширину є визначення$\Delta \omega=\omega_{+}-\omega_{-}$, де$\omega_{\pm}$ знаходяться значення кутової частоти, такі, що усереднена за часом енергія дорівнює половині її максимального значення.

$$\left\langle E\left(\omega_{\pm}\right)\right\rangle=\frac{1}{2}\left\langle E\left(\omega_{0}\right)\right\rangle=\frac{m F_{0}^{2}}{4 b^{2}} \nonumber$$

Величина$\Delta \omega$ називається шириною лінії при половині максимуму енергії також відомий як ширина резонансу. Тепер ми можемо вирішити для$\omega_{\pm}$, встановивши

$$\left\langle E\left(\omega_{\pm}\right)\right\rangle=\frac{F_{0}^{2}}{2 m} \frac{1}{\left((b / m)^{2}+4\left(\omega_{0}-\omega_{\pm}\right)^{2}\right)}=\frac{m F_{0}^{2}}{4 b^{2}} \nonumber$$

поступаючись умові, що

$$(b / m)^{2}=4\left(\omega_{0}-\omega_{\pm}\right)^{2} \nonumber$$

Взяття квадратних коренів рівняння (23.6.49) дає

$$\mp(b / 2 m)=\omega_{0}-\omega_{\pm} \nonumber$$

Тому

$$\omega_{\pm}=\omega_{0} \pm(b / 2 m) \nonumber$$

Половина ширини тоді

$$\Delta \omega=\omega_{+}-\omega_{-}=\left(\omega_{0}+(b / 2 m)\right)-\left(\omega_{0}-(b / 2 m)\right)=b / m \nonumber$$

Визначено якість Q резонансу як відношення резонансної кутової частоти до ширини лінії,

$$Q=\frac{\omega_{0}}{\Delta \omega}=\frac{\omega_{0}}{b / m} \nonumber$$

Малюнок 23.21 Графік усередненої за часом енергії проти кутової частоти для різних значень$b / m$

На малюнку 23.21 ми будуємо усереднену за часом енергію проти кутової частоти для декількох різних значень коефіцієнта якості Q = 10, 5 та 3. Нагадаємо, що це був той самий результат, який ми мали для якості вільних коливань затухаючого осцилятора, Equation (23.5.16) (тому що ми вибрали коефіцієнт$\pi$ в Equation (23.5.16)).