23.5: Затухаючий коливальний рух

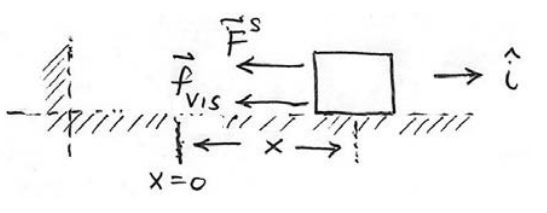
Розглянемо тепер нашу пружинно-блокову систему, що рухається по горизонтальній поверхні без тертя, але тепер блок прикріплений до заслінки, яка чинить опір руху блоку за рахунок в'язкого тертя. Цей демпфер, який прийнято називати приладовим пристроєм, показаний на малюнку 23.13. В'язка сила виникає, коли предмети рухаються по рідинам зі швидкостями досить повільно, щоб не було турбулентності. Коли в'язка сила протистоїть руху і пропорційна швидкості, так що

\[\overrightarrow{\mathbf{f}}_{\mathrm{vis}}=-b \overrightarrow{\mathbf{v}} \nonumber \]

dashpot називається лінійним приладовим пристроєм. Константа пропорційності b залежить від властивостей приладової точки.

Малюнок 23.12 Пружинно-блокова система, підключена до лінійної приладової точки

Виберіть початок в положенні рівноваги і виберіть позитивне х -напрямок вправо на малюнку 23.13. Визначте,\(x(t)\) щоб бути положення об'єкта щодо положення рівноваги. Х -складова сумарної сили, що діє на пружину, є сумою лінійної відновлювальної сили пружини, а сили в'язкого тертя (рис. 23.13),

\[F_{x}=-k x-b \frac{d x}{d t} \nonumber \]

Малюнок 23.13 Діаграма сили вільного тіла для системи пружинних об'єктів з лінійною приладовою точкою

Другий закон Ньютона в х -напрямку стає

\[-k x-b \frac{d x}{d t}=m \frac{d^{2} x}{d t^{2}} \nonumber \]

Ми можемо переписати рівняння (23.5.3) як

\[\frac{d^{2} x}{d t^{2}}+\frac{b}{m} \frac{d x}{d t}+\frac{k}{m} x=0 \nonumber \]

Коли\((b / m)^{2}<4 k / m\) осцилятор називається underdamped, а рішення Рівняння (23.5.4) задається

\[x(t)=x_{\mathrm{m}} e^{-\alpha t} \cos (\gamma t+\phi) \nonumber \]

де\(\gamma=\left(k / m-(b / 2 m)^{2}\right)^{1 / 2}\) - кутова частота коливань,\(\alpha=b / 2 m\) - параметр, який вимірював експоненціальний розпад коливань\(x_{\mathrm{m}}\), є постійною і\(\phi\) є фазною постійною. Нагадаємо, що осцилятор не затухає має кутову частоту\(\omega_{0}=(k / m)^{1 / 2}\), тому кутова частота низькозатухаючого генератора може бути виражена як

\[\gamma=\left(\omega_{0}^{2}-\alpha^{2}\right)^{1 / 2} \nonumber \]

У Додатку 23B: Комплексні числа ми вводимо комплексні числа та використовуємо їх для розв'язання рівняння (23.5.4) у Додатку 23C: Розв'язок слабкого простого гармонійного рівняння осцилятора.

x -складова швидкості об'єкта задається

\[v_{x}(t)=d x / d t=\left(-\gamma x_{\mathrm{m}} \sin (\gamma t+\phi)-\alpha x_{\mathrm{m}} \cos (\gamma t+\phi)\right) e^{-\alpha t} \nonumber \]

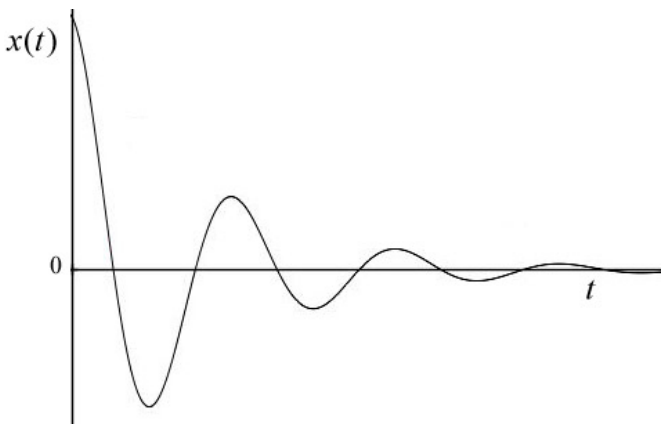
Положення і х -складова швидкості об'єкта коливаються, але амплітуди коливань експоненціально зникають. На малюнку 23.14 положення побудовано як функція часу для недогашенной системи для особливого випадку\(\phi=0\). Для цього випадку

\[x(t)=x_{\mathrm{m}} e^{-\alpha t} \cos (\gamma t) \nonumber \]

і

\[v_{x}(t)=d x / d t=\left(-\gamma x_{\mathrm{m}} \sin (\gamma t)-\alpha x_{\mathrm{m}} \cos (\gamma t)\right) e^{-\alpha t} \nonumber \]

Малюнок 23.14 Ділянка положення x (t) об'єкта для низькозатухаючого осцилятора з φ = 0

Оскільки коефіцієнт експоненціального розпаду\(\alpha=b / 2 m\) пропорційний b, ми бачимо, що положення буде слабшати швидше, якщо в'язка сила збільшиться. Ми можемо ввести постійну часу

\[\tau=1 / \alpha=2 m / b \nonumber \]

Коли\(t=\tau\), посада

\[x(t=\tau)=x_{\mathrm{m}} \cos (\gamma \tau) e^{-1} \nonumber \]

Огинаюча експоненціального розпаду тепер зменшується в рази\(e^{-1}\), тобто амплітуда може бути не більше\(x_{\mathrm{m}} e^{-1}\). За цей часовий проміжок\([0, \tau]\) положення зазнало ряд коливань. Загальна кількість радіанів, пов'язаних з цими коливаннями, задається

\[\gamma \tau=\left(k / m-(b / 2 m)^{2}\right)^{1 / 2}(2 m / b) \nonumber \]

Найближче інтегральне число циклів тоді

\[n=[\gamma \tau / 2 \pi]=\left[\left(k / m-(b / 2 m)^{2}\right)^{1 / 2}(m / \pi b)\right] \nonumber \]

Якщо система дуже слабо затухає, така що\((b / m)^{2}<<4 k / m\), то можна наблизити кількість циклів по

\[n=[\gamma \tau / 2 \pi] \simeq\left[(k / m)^{1 / 2}(m / \pi b)\right]=\left[\omega_{0}(m / \pi b)\right] \nonumber \]

де\(\omega_{0}=(k / m)^{1 / 2}\) - кутова частота осцилятора, що не затухає.

Визначено якість, Q, цієї коливальної системи пропорційно кількості інтегральних циклів, які потрібно для того, щоб експоненціальна оболонка функції положення відпала на множник\(e^{-1}\). Константа пропорційності вибирається бути\(\pi\). Таким чином

\[Q=n \pi \nonumber \]

Для слабко демпфірованого випадку ми маємо, що

\[Q \simeq \omega_{0}(m / b) \nonumber \]

Енергія в осциляторі з низьким затуханням

Для недогашеного осцилятора\((b / m)^{2}<4 k / m, \quad \gamma=\left(k / m-(b / 2 m)^{2}\right)^{1 / 2}\), і\(\alpha=b / 2 m\). Давайте виберемо\(t=0\) такий, щоб зсув фаз\(\phi=0\) дорівнював нулю. НаКОПИЧЕНА енергія в системі буде падати через втрати енергії внаслідок розсіювання. Механічна енергія, що зберігається в потенційній та кінетичній енергіях, потім задається

\[E=\frac{1}{2} k x^{2}+\frac{1}{2} m v^{2} \nonumber \]

де положення і х -складова швидкості задаються рівняннями (23.5.8) і (23.5.9). Механічна енергія тоді

\[E=\frac{1}{2} k x_{\mathrm{m}}^{2} \cos ^{2}(\gamma t) e^{-2 \alpha t}+\frac{1}{2} m\left(-\gamma x_{\mathrm{m}} \sin (\gamma t)-\alpha x_{\mathrm{m}} \cos (\gamma t)\right)^{2} e^{-2 \alpha t} \nonumber \]

Розширення цього виразу дає

\[E=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \cos ^{2}(\gamma t) e^{-2 \alpha t}+m \gamma \alpha x_{\mathrm{m}}^{2} \sin (\gamma t) \cos (\gamma t) e^{-2 \alpha t}+\frac{1}{2} m \gamma^{2} x_{\mathrm{m}}^{2} \sin ^{2}(\gamma t) e^{-2 \alpha t} \nonumber \]

Кінетична енергія, потенційна енергія та механічна енергія показані на малюнку 23.15.

Малюнок 23.15 Кінетична, потенційна та механічна енергія для осцилятора з низьким затуханням

Накоплена енергія в момент t = 0 дорівнює

\[E(t=0)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} \nonumber \]

Механічна енергія при укладенні одного циклу, з\(\gamma T=2 \pi\), становить

\[E(t=T)=\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2} e^{-2 \alpha T} \nonumber \]

Зміна механічної енергії за один цикл

\[E(t=T)-E(t=0)=-\frac{1}{2}\left(k+m \alpha^{2}\right) x_{\mathrm{m}}^{2}\left(1-e^{-2 \alpha T}\right) \nonumber \]

Нагадаємо, що\(\alpha^{2}=b^{2} / 4 m^{2}\). Тому

\[E(t=T)-E(t=0)=-\frac{1}{2}\left(k+b^{2} / 4 m\right) x_{\mathrm{m}}^{2}\left(1-e^{-2 \alpha T}\right) \nonumber \]

Ми можемо показати (хоча розрахунок тривалий), що енергія, розсіяна в'язкою силою за один цикл, задається інтегралом

\[E_{\mathrm{dis}}=\int_{0}^{T} \overrightarrow{\mathbf{F}}_{\mathrm{vis}} \cdot \overrightarrow{\mathbf{v}} d t=-\left(k+\frac{b^{2}}{4 m}\right) \frac{x_{\mathrm{m}}^{2}}{2}\left(1-e^{-2 \alpha t}\right) \nonumber \]

Порівняно з рівнянням (23.5.23), зміна механічної енергії в недогашеному осциляторі протягом одного циклу дорівнює енергії, що розсіюється за рахунок в'язкої сили протягом одного циклу.