23.4: Опрацьовані приклади

Приклад 23.3: Прокатка без ковзання коливального циліндра

Прикріпіть суцільний циліндр масою М і радіусом R до горизонтальної безмасової пружини з постійною пружини k, щоб він міг котитися, не ковзаючи по горизонтальній поверхні. У момент t центр маси циліндра рухається зі швидкістю$V_{c m}$ і пружина стискається vθ ,1 = ± 2gl (1− cosθ 0). відстань x від його рівноважної довжини. Який період простого гармонійного руху для центру мас циліндра?

Малюнок 23.9 Приклад 23.3

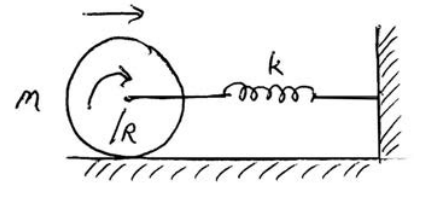
Рішення: Під час t енергія прокатного циліндра та пружинної системи становить

$$E=\frac{1}{2} M v_{c m}^{2}+\frac{1}{2} I_{c m}\left(\frac{d \theta}{d t}\right)^{2}+\frac{1}{2} k x^{2} \nonumber$$

де x - величина, яку пружина стисла$I_{c m}=(1 / 2) M R^{2}$, і тому що вона котиться без ковзання

$$\frac{d \theta}{d t}=\frac{V_{c m}}{R} \nonumber$$

Тому енергія є

$$E=\frac{1}{2} M V_{c m}^{2}+\frac{1}{4} M R^{2}\left(\frac{V_{c m}}{R}\right)^{2}+\frac{1}{2} k x^{2}=\frac{3}{4} M V_{c m}^{2}+\frac{1}{2} k x^{2} \nonumber$$

Енергія постійна (ніяка неконсервативна сила не робить роботу над системою) тому

$$0=\frac{d E}{d t}=\frac{3}{4} 2 M V_{c m} \frac{d V_{c m}}{d t}+\frac{1}{2} k 2 x \frac{d x}{d t}=V_{c m}\left(\frac{3}{2} M \frac{d^{2} x}{d t^{2}}+k x\right) \nonumber$$

Оскільки$V_{c m}$ більшу частину часу ненульовий, зміщення пружини задовольняє просте рівняння гармонічного осцилятора

$$\frac{d^{2} x}{d t^{2}}+\frac{2 k}{3 M} x=0 \nonumber$$

Звідси період

$$T=\frac{2 \pi}{\omega_{0}}=2 \pi \sqrt{\frac{3 M}{2 k}} \nonumber$$

Приклад 23.4: U-трубка

U-трубка, відкрита з обох кінців, заповнена нестисливою рідиною щільності$\rho$. Площа поперечного перерізу А трубки рівномірна, а загальна довжина рідини в трубці дорівнює L. Поршень використовується для натискання висоти стовпа рідини з одного боку на відстань$x_{0}$ (підняття іншої сторони на таку ж відстань), а потім швидко знімається (рис. 23.10). Яка кутова частота послідовного простого гармонійного руху? Нехтують будь-якими резистивними силами і біля стінок U-трубки.

Малюнок 23.11 Енергетична діаграма для води

Рішення: Ми будемо використовувати збереження енергії. Спочатку вибирайте як нуль для гравітаційної потенційної енергії в конфігурації, де рівні води рівні по обидва боки трубки. Коли поршень з одного боку пригнічує рідину, вона піднімається з іншого. У даний момент часу, коли частина рідини маси$\Delta m=\rho A x$ знаходиться на висоті х вище рівноважної висоти (рис. 23.11), потенційна енергія рідини задається

$$U=\Delta m g x=(\rho A x) g x=\rho \operatorname{Ag} x^{2} \nonumber$$

У той же момент вся рідина довжини L і маси$m=\rho A L$ рухається зі швидкістю v, тому кінетична енергія

$$K=\frac{1}{2} m v^{2}=\frac{1}{2} \rho A L v^{2} \nonumber$$

Таким чином, загальна енергія

$$E=K+U=\frac{1}{2} \rho A L v^{2}+\rho A g x^{2} \nonumber$$

Нехтуючи резистивною силою, механічна енергія рідини постійна. Тому

$$0=\frac{d E}{d t}=\rho A L v \frac{d v}{d t}+2 \rho \operatorname{Ag} x \frac{d x}{d t} \nonumber$$

Якщо ми просто розглянемо верхню частину рідини над положенням рівноваги на правій руці на малюнку 23.13, ми перепишемо Рівняння (23.4.10) як

$$0=\frac{d E}{d t}=\rho A L v_{x} \frac{d v_{x}}{d t}+2 \rho A g x \frac{d x}{d t} \nonumber$$

де$v_{x}=d x / d t$. Тепер ми перепишемо енергетичний стан$d v_{x} / d t=d^{2} x / d t^{2}$, використовуючи як

$$0=v_{x} \rho A\left(L \frac{d^{2} x}{d t^{2}}+2 g x\right) \nonumber$$

Ця умова виконується, коли$v_{x}=0$ тобто умова рівноваги або коли

$$0=L \frac{d^{2} x}{d t^{2}}+2 g x \nonumber$$

Ця остання умова може бути записана як

$$\frac{d^{2} x}{d t^{2}}=-\frac{2 g}{L} x \nonumber$$

Це останнє рівняння є простим рівнянням гармонічного осцилятора. Використовуючи ті ж математичні прийоми, які ми використовували для системи пружинних блоків, рішення висоти рідини над положенням рівноваги задається

$$x(t)=B \cos \left(\omega_{0} t\right)+C \sin \left(\omega_{0} t\right) \nonumber$$

де

$$\omega_{0}=\sqrt{\frac{2 g}{L}} \nonumber$$

- кутова частота коливань. Х -складова швидкості рідини з правого боку U-трубки задається

$$v_{x}(t)=\frac{d x(t)}{d t}=-\omega_{0} B \sin \left(\omega_{0} t\right)+\omega_{0} C \cos \left(\omega_{0} t\right) \nonumber$$

Коефіцієнти В і С визначаються початковими умовами. $t=0$На висоті знаходиться рідина$x(t=0)=B=x_{0}$. При$t=0$, швидкість дорівнює нулю так$v_{x}(t=0)=\omega_{0} C=0$, отже$C=0$. Таким чином, висота рідини над положенням рівноваги на правій стороні U-трубки як функція часу

$$x(t)=x_{0} \cos (\sqrt{\frac{2 g}{L}} t) \nonumber$$