19.6: Кутовий момент системи частинок

Тепер обчислюємо момент моменту навколо точки,$S$ пов'язаної з системою N точкових частинок. Позначте кожну окрему частинку індексом$j, j=1,2, \cdots, N$. Нехай$j^{\mathrm{th}}$ частинка має масу$m_{j}$ і швидкість$\overrightarrow{\mathbf{V}}$. Імпульс окремої частинки тоді$\overrightarrow{\mathbf{p}}_{j}=m_{j} \overrightarrow{\mathbf{v}}_{j}$. $\overrightarrow{\mathbf{r}}_{S, j}$Дозволяти вектор від точки$S$ до$j^{\mathrm{th}}$ частинки, і$\theta_{j}$ нехай кут між векторами$\overrightarrow{\mathbf{r}}_{S, j}$ і$\overrightarrow{\mathbf{p}}_{j}$ (рис. 19.10).

Малюнок$\PageIndex{1}$: Система частинок

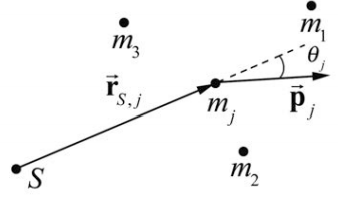
Кутовий$\overrightarrow{\mathbf{L}}_{S, j}$ імпульс$j^{\text {th }}$ частинки дорівнює

$$\overrightarrow{\mathbf{L}}_{S, j}=\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{p}}_{j} \nonumber$$

Кутовий момент для системи частинок - векторна сума окремих кутових моментів,

$$\overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}=\sum_{j=1}^{i=N} \overrightarrow{\mathbf{L}}_{S, j}=\sum_{j=1}^{i=N} \overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{p}}_{j} \nonumber$$

Зміна кутового моменту системи частинок близько точки$S$ задається

$$\frac{d \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}}{d t}=\frac{d}{d t} \sum_{j=1}^{j=N} \overrightarrow{\mathbf{L}}_{S, j}=\sum_{j=1}^{j=N}\left(\frac{d \overrightarrow{\mathbf{r}}_{S, j}}{d t} \times \overrightarrow{\mathbf{p}}_{j}+\overrightarrow{\mathbf{r}}_{S, j} \times \frac{d \overrightarrow{\mathbf{p}}_{j}}{d t}\right) \nonumber$$

Оскільки швидкість$j^{\text {th }}$ частинки є$\overrightarrow{\mathbf{v}}_{S, j}=d{\mathbf{r}}_{S, j} / d t$, перший член в дужках зникає (перехресний добуток вектора з самим собою дорівнює нулю, оскільки вони паралельні один одному)

$$\frac{d \overrightarrow{\mathbf{r}}_{S, j}}{d t} \times \overrightarrow{\mathbf{p}}_{j}=\overrightarrow{\mathbf{v}}_{S, j} \times m_{j} \overrightarrow{\mathbf{v}}_{S, j}=0 \nonumber$$

Рівняння заміни (19.5.4) і$\overrightarrow{\mathbf{F}}_{j}=d \overrightarrow{\mathbf{p}}_{j} / d t$ в рівняння (19.5.3), що дає

$$\frac{d \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}}{d t}=\sum_{j=1}^{i=N}\left(\overrightarrow{\mathbf{r}}_{S, j} \times \frac{d \overrightarrow{\mathbf{p}}_{j}}{d t}\right)=\sum_{j=1}^{i=N}\left(\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{F}}_{j}\right) \nonumber$$

Тому що

$$\sum_{j=1}^{j=N}\left(\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{F}}_{j}\right)=\sum_{j=1}^{j=N} \vec{\tau}_{S, j}=\vec{\tau}_{S}^{\mathrm{ext}}+\vec{\tau}_{S}^{\mathrm{int}} \nonumber$$

Ми вже показали в главі 17.4, що коли ми припускаємо, що всі внутрішні сили спрямовані τ уздовж лінії, що з'єднує два взаємодіючих об'єкта, то внутрішній крутний момент навколо точки$S$ дорівнює нулю,

$$\vec{\tau}_{S}^{\mathrm{int}}=\overrightarrow{\boldsymbol{0}} \nonumber$$

Рівняння (19.5.6) спрощує

$$\sum_{j=1}^{i=N}\left(\overrightarrow{\mathbf{r}}_{S, j} \times \overrightarrow{\mathbf{F}}_{j}\right)=\sum_{j=1}^{j=N} \vec{\tau}_{S, j}=\vec{\tau}_{S}^{\mathrm{ext}} \nonumber$$

Тому рівняння (19.5.5) стає

$$\vec{\tau}_{S}^{\mathrm{ext}}=\frac{d \overrightarrow{\mathbf{L}}_{S}^{\mathrm{sys}}}{d t} \nonumber$$

Зовнішній крутний момент$S$ навколо точки дорівнює тимчасовій похідній моменту моменту системи про цю точку.

Приклад$\PageIndex{1}$: Angular Momentum of Two Particles undergoing Circular Motion

Дві однакові частинки масою m рухаються по колу радіусом R$\vec{\omega}=\omega_{z} \hat{\mathbf{k}}, \omega_{z}>0$, з кутовою швидкістю,$\omega$ навколо осі z в площині, паралельній відстані h над площиною x-y. Частинки розташовуються з протилежних сторін кола (рис. 19.11). Знайдіть величину і напрямок кутового моменту про точку$S$ (початок).

Малюнок 19.11 Приклад 19.5

Рішення

Кутовий момент про походження - це сума внесків від кожного об'єкта. Розрахунок кожного внеску буде ідентичним розрахунку в прикладі 19.3

Малюнок 19.12 Кутовий момент частинки 1 про походження

Малюнок 19.13 Кутовий момент частинки 2 про походження

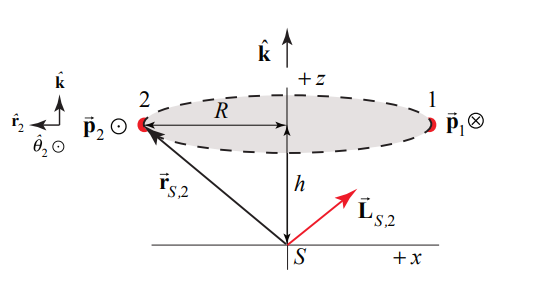
Для частинки 1 (рис. 19.12) кутовий момент моменту навколо точки$S$ дорівнює

$$\overrightarrow{\mathbf{L}}_{S, 1}=\overrightarrow{\mathbf{r}}_{S, 1} \times \overrightarrow{\mathbf{p}}_{1}=\left(R \hat{\mathbf{r}}_{1}+h \hat{\mathbf{k}}\right) \times m R \omega_{z} \hat{\mathbf{\theta}}_{1}=m R^{2} \omega_{z} \hat{\mathbf{k}}-h m R \omega_{z} \hat{\mathbf{r}}_{1} \nonumber$$

Для частинки 2 (рис. 19.13) кутовий момент моменту навколо точки$S$ дорівнює

$$\overrightarrow{\mathbf{L}}_{S, 2}=\overrightarrow{\mathbf{r}}_{S, 2} \times \overrightarrow{\mathbf{p}}_{2}=\left(R \hat{\mathbf{r}}_{2}+h \hat{\mathbf{k}}\right) \times m R \omega_{z} \hat{\mathbf{\theta}}_{2}=m R^{2} \omega_{z} \hat{\mathbf{k}}-h m R \omega_{z} \hat{\mathbf{r}}_{2} \nonumber$$

Тому що частинки розташовані по протилежних сторонам кола,$\hat{\mathbf{r}}_{1}=-\hat{\mathbf{r}}_{2}$. Векторна сума лише вказує вздовж осі z і дорівнює

$$\overrightarrow{\mathbf{L}}_{s}=\overrightarrow{\mathbf{L}}_{S, 1}+\overrightarrow{\mathbf{L}}_{S, 2}=2 m R^{2} \omega_{z} \hat{\mathbf{k}} \nonumber$$

Два вектори кутового моменту показані на малюнку 19.14.

Малюнок 19.14 Кутовий момент моменту$S$ про точку обох частинок і їх сума

Момент інерції двох частинок навколо осі z задається$I_{S}=2 m R^{2}$. Тому$\overrightarrow{\mathbf{L}}_{S}=I_{S} \vec{\omega}$. Важливим моментом цього прикладу є те, що два об'єкти симетрично розподілені по відношенню до осі z (протилежні сторони кругової орбіти). Тому кутовий момент навколо будь-якої точки$S$ вздовж осі z має однакове значення,$\overrightarrow{\mathbf{L}}_{s}=2 m r^{2} \omega \hat{\mathbf{k}}$ яке є постійним за величиною і вказує в + z -напрямку. Цей результат узагальнюється до будь-якого жорсткого тіла, в якому маса розподілена симетрично щодо осі обертання.

Приклад$\PageIndex{2}$: Angular Momentum of a System of Particles about Different Points

Розглянемо систему з N частинок, а також дві точки А і В (рис. 19.15). Кутовий імпульс$j^{i h}$ частинки близько точки А задається

$$\overrightarrow{\mathbf{L}}_{A, j}=\overrightarrow{\mathbf{r}}_{A, j} \times m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

Малюнок 19.15 Векторний трикутник, що пов'язує положення об'єкта і точок A і B

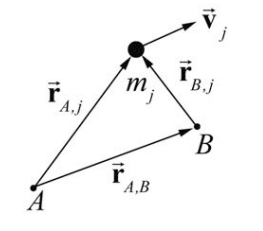
Кутовий момент системи частинок про точку А задається сумою

$$\overrightarrow{\mathbf{L}}_{A}=\sum_{j=1}^{N} \overrightarrow{\mathbf{L}}_{A, j}=\sum_{j=1}^{N} \overrightarrow{\mathbf{r}}_{A, j} \times m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

Кутовий момент навколо точки В може бути розрахований аналогічним чином і задається

$$\overrightarrow{\mathbf{L}}_{B}=\sum_{j=1}^{N} \overrightarrow{\mathbf{L}}_{B, j}=\sum_{j=1}^{N} \overrightarrow{\mathbf{r}}_{B, j} \times m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

З малюнка 19.15 вектори

$$\overrightarrow{\mathbf{r}}_{A, j}=\overrightarrow{\mathbf{r}}_{B, j}+\overrightarrow{\mathbf{r}}_{A, B} \nonumber$$

Ми можемо замінити рівняння (19.5.14) на рівняння (19.5.12), що дає

$$\overrightarrow{\mathbf{L}}_{A}=\sum_{j=1}^{N}\left(\overrightarrow{\mathbf{r}}_{B, j}+\overrightarrow{\mathbf{r}}_{A, B}\right) \times m_{j} \overrightarrow{\mathbf{v}}_{j}=\sum_{j=1}^{N} \overrightarrow{\mathbf{r}}_{B, j} \times m_{j} \overrightarrow{\mathbf{v}}_{j}+\sum_{j=1}^{N} \overrightarrow{\mathbf{r}}_{A, B} \times m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

Перший член у Рівнянні (19.5.15) - це кутовий момент навколо точки B. Вектор$\overrightarrow{\mathbf{r}}_{A, B}$ є константою і тому може бути витягнутий з суми у другому семестрі, а Рівняння (19.5. 15) стає

$$\overrightarrow{\mathbf{L}}_{A}=\overrightarrow{\mathbf{L}}_{B}+\overrightarrow{\mathbf{r}}_{A, B} \times \sum_{j=1}^{N} m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

Сума в другому семестрі - імпульс системи

$$\overrightarrow{\mathbf{p}}_{\mathrm{sys}}=\sum_{j=1}^{N} m_{j} \overrightarrow{\mathbf{v}}_{j} \nonumber$$

Тому кутовий імпульс про точки А і В пов'язані між собою

$$\overrightarrow{\mathbf{L}}_{A}=\overrightarrow{\mathbf{L}}_{B}+\overrightarrow{\mathbf{r}}_{A, B} \times \overrightarrow{\mathbf{p}}_{\mathrm{sys}} \nonumber$$

Таким чином, якщо імпульс системи дорівнює нулю, кутовий момент однаковий щодо будь-якої точки.

$$\overrightarrow{\mathbf{L}}_{A}=\overrightarrow{\mathbf{L}}_{B}, \quad\left(\overrightarrow{\mathbf{p}}_{\mathrm{sys}}=\overrightarrow{\mathbf{0}}\right) \nonumber$$

Зокрема, імпульс системи частинок дорівнює нулю за визначенням у центрі системи відліку мас, оскільки в цій системі відліку$\overrightarrow{\mathbf{p}}_{\mathrm{sys}}=\overrightarrow{\mathbf{0}}$. Звідси кутовий імпульс однаковий щодо будь-якої точки в центрі системи відліку маси.