19.8: Принцип збереження кутового моменту

Розглянемо систему частинок. Почнемо з результату, який ми вивели в розділі 19.7, що крутний момент близько точки\(S\) дорівнює часовій похідній від моменту моменту моменту про цю точку S,

\ почати {рівняння}\ vec {\ тау} _ {S} ^ {\ mathrm {ext}} =\ frac {d\ overrightarrow {\ mathbf {L}} _ {S} ^ {\ mathrm {sys}}} {d t}\ кінець {рівняння}

При такому припущенні крутний момент, обумовлений зовнішніми силами, дорівнює швидкості зміни кутового моменту.

\ begin {рівняння}\ vec {\ tau} _ {S} ^ {\ mathrm {ext}} =\ frac {d\ overrightarrow {\ mathrm {L}} _ {S} ^ {\ mathrm {sys}}} {d t}\ кінець {рівняння}

Принцип збереження кутового моменту

Якщо зовнішній крутний момент, що діє на систему, дорівнює нулю, то кутовий момент системи постійний. Так що при будь-якій зміні стану системи зміна кутового моменту дорівнює нулю.

\ begin {рівняння}\ Дельта\ переправа стрілка {\ mathbf {L}} _ {S} ^ {\ mathrm {sys}}\ equiv\ ліворуч (\ mathbf {L}} _ {S} ^ {\ mathrm {sys}}\ праворуч) _ {f} -\ ліворуч (\ overrightarrow {\ mathbr {\ mathbrow {\ mathbr f {L}} _ {S} ^ {\ mathrm {sys}}\ праворуч) _ {i} =\ overrightarrow {\ mathbf {0}}\ кінець {рівняння}

Рівнозначно кутовий імпульс постійний.

\ почати {рівняння}\ ліворуч (\ overrightarrow {\ mathbf {L}} _ {S} ^ {\ mathrm {sys}}\ праворуч) _ {f} =\ ліворуч (\ переправа стрілка {\ mathbf {L}} _ {S} ^ {\ mathrm {sys}}\ праворуч) _ {i}\ кінець {рівняння}

Поки що не було виявлено жодної ізольованої системи, що кутовий імпульс не є постійним, тому наше припущення, що внутрішні крутні моменти скасовують пари, можна сприймати як експериментальне спостереження.

Приклад\(\PageIndex{1}\): Collision Between Pivoted Rod and Object

Точковий об'єкт маси, що\(m_{1}\) рухається з постійною швидкістю,\(v_{i}\) вражає жорсткий рівномірний стрижень довжиною l і масою\(m_{2}\), який звисає безфрикційним шарніром зі стелі. Відразу після удару по штоку об'єкт продовжує рух вперед, але швидкість його зменшується до\(v_{i} / 2\) (рис. 19.19). Момент інерції стрижня про його центр мас дорівнює

\[I_{c m}=(1 / 12) m_{2} l^{2} \nonumber \]

Гравітація діє з прискоренням g вниз.

1. (а) Для якого значення стрижень\(v_{i}\) буде просто торкатися стелі на його першому гойдалку?
2. (б) Для якого співвідношення зіткнення\(m_{2} / m_{1}\) буде еластичним?

Малюнок 19.19 Приклад 19.7

Рішення

Починаємо з ідентифікації нашої системи, яка складається з об'єкта і рівномірного стрижня. Виділяємо три стани; початковий стан i: безпосередньо перед зіткненням стан a: відразу після зіткнення, і стан f: момент дотику стрижня до стелі, коли кінцева кутова швидкість дорівнює нулю. Ми хотіли б знати, чи є будь-яка з наших фундаментальних величин: імпульс, енергія та момент імпульсу постійними під час цих змін стану, стан i до стану a, стан a до стану f.

Малюнок 19.20 Діаграми сили вільного тіла на частинці та стрижні

Почнемо з переходу від стану i до стану a. Сила повороту, що утримує стрижень до стелі, - це зовнішня сила, що діє в точці повороту\(S\). Існує також гравітаційна сила, що діє в центрі мас стрижня і на предмет. Існують також внутрішні сили внаслідок зіткнення стрижня і об'єкта в точці А (рис. 19.20).

Зовнішня сила означає, що імпульс не є постійним. Точка дії зовнішньої сили повороту фіксована і тому не працює. Однак ми не знаємо, чи є зіткнення еластичним, і тому ми не можемо припустити, що механічна енергія постійна. Виберіть точку повороту в\(S\) якості точки, про яку слід розрахувати крутний момент, тоді діаграми крутного моменту наведені на малюнку 19.21.

Малюнок 19.21 Діаграми крутного моменту на частинці та стрижні з крутним моментом, розрахованим щодо точки повороту S

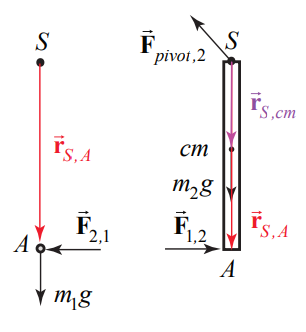
Крутний момент на системі про\(S\) шкворню - це сума термінів

\ почати {рівняння}\ vec {\ тау} _ {S} ^ {\ mathrm {sys}} =\ переправа стрілка {\ mathbf {r}} _ {S, S}\ раз\ переправа {\ mathbf {F}} _ {\ текст {pivot}, 2} +\ переправа {\ mathbf {r} {_ S, A}\ times\ overrightarrow {\ mathbf {F}} _ {1,2} +\ переправа {\ mathbf {r}} _ {S, A}\ times\ overrightarrow {\ mathbf {F}} _ {2,1} +\ mathbf {r} _ {S, c m}\ раз m_ {2}\ переправа стрілка {\ mathbf {g}} +\ переправа стрілка {\ mathbf {r}} _ {S, A}\ times m_ {1}\ переправа стрілка {\ mathbf {g}}\ cdot (19.5 .37)\ кінець {рівняння}

Зовнішня сила повороту не сприяє жодному крутному моменту, тому що\(\overrightarrow{\mathbf{r}}_{S, S}=\overrightarrow{\mathbf{0}}\). Внутрішні сили між стрижнем і предметом рівні за величиною і протилежні в напрямку,\(\overrightarrow{\mathbf{F}}_{1,2}=-\overrightarrow{\mathbf{F}}_{2,1}\) (Третій закон Ньютона), і тому їх внески в крутний момент додають до нуля. Якщо зіткнення миттєве, то гравітаційна сила паралельна\(\overrightarrow{\mathbf{r}}_{S, c m} \text { and } \overrightarrow{\mathbf{r}}_{S, A}\) тому два гравітаційних моменту дорівнюють нулю. Тому крутний момент на системі про точку повороту дорівнює нулю,\(\vec{\tau}_{S}^{\mathrm{sys}}=\overrightarrow{0}\). Таким чином, кутовий імпульс навколо точки повороту постійний,

\ почати {рівняння}\ переправа стрілка {\ mathbf {L}} _ {S, i} ^ {\ mathrm {sys}} =\ overrightarrow {\ mathbf {L}} _ {S, a} ^ {\ mathrm {sys}}\ кінець {рівняння}

Малюнок 19.22 Діаграма кутового моменту

Для того щоб розрахувати кутовий момент, намалюємо діаграму, що показує імпульс об'єкта і кутову швидкість стрижня в (рис. 19.22). Кутовий імпульс приблизно\(S\) безпосередньо перед зіткненням

\ почати {рівняння}\ переправа стрілка {\ mathbf {L}} _ {S, i} ^ {\ mathrm {sys}} =\ переправа стрілка {\ mathbf {r}} _ {S, 1}\ times m_ {1}\ overrightarrow {\ mathbf {v}} _ {i} =л (-\ hat {\ mathbf {v}} _ {i} =л (-\ hat {\ mathbf thbf {j}})\ раз m_ {1} v\ hat {\ mathbf {i}} =\ ім'я оператора {lm} _ {1} v\ hat {\ mathbf {k}}\ end {рівняння}

Кутовий імпульс приблизно\(S\) відразу після зіткнення

\ почати {рівняння}\ переправа стрілка {\ mathbf {L}} _ {S, a} ^ {\ mathrm {ys}} =\ переправа стрілка {\ mathbf {r}} _ {S, 1}\ times m_ {1}\ переправа {\ mathbf {v}} _ {i}/2+_ {S} переправа стрілка {\ напівжирний символ {\ омега}} _ {a} =л (-\ капелюх {\ mathbf {j}})\ раз м_ {1}\ ліворуч (v_ {i}/2\ праворуч)\ капелюх {\ mathbf {i}} +I_ {s}\ omega_ {a}\ hat {\ mathbf {k}} = лівий (л м_ {1} v_ {i}/2\ право)\ hat {\ mathbf {k}} +I_ {s}\ омега_ {a}\ hat {\ mathbf {k}}\ кінець {рівняння}

Тому умова, що момент імпульсу близько\(S\) постійний під час зіткнення, стає.

\ begin {рівняння}\ ім'я оператора {lm} _ {1} v_ {i}\ hat {\ mathbf {k}} =\ лівий (\ ім'я оператора {lm} _ {1} v_ {i}/2+I_ {s}\ omega_ {a}\ праворуч)\ капелюх {\ mathbf {k}}\ кінець {рівняння}

Ми можемо вирішити кутову швидкість відразу після зіткнення

\ begin {рівняння}\ омега_ {a} =\ frac {\ ім'я оператора {lm} _ {1} v_ {i}} {2 I_ {S}}\ end {рівняння}

\ begin {рівняння}\ омега_ {a} =\ frac {l m_ {1} v_ {i}} {2 I_ {S}}\ кінець {рівняння}

За теоремою паралельної осі момент інерції рівномірного стрижня навколо точки повороту дорівнює

\ почати {рівняння} I_ {S} =м_ {2} (л/2) ^ {2} +I_ {c м} = (1/4) m_ {2} l^ {2} + (1/12) m_ {2} l^ {2} = (1/3) m_ {2} l^ {2}\ кінець {рівняння}

Тому кутова швидкість відразу після зіткнення

\ begin {рівняння}\ омега_ {2} =\ frac {3 m_ {1} v_ {i}} {2 m_ {2} l}\ end {рівняння}

Малюнок 19.23 Енергетична діаграма для переходу від стану a до стану f.

Для переходу від стану a до стану f ми знаємо, що сила тяжіння консервативна, а сила повороту не працює, тому механічна енергія постійна.

\ begin {рівняння} E_ {a} ^ {m e c h} =E_ {f} ^ {m e c h}\ end {рівняння}

Намалюємо енергетичну діаграму тільки для стрижня, оскільки кінетична енергія для частинки не змінюється між станами a і f, (рис. 19.23), з вибором нуля для потенційної енергії в центрі мас. Механічна енергія стрижня і частинки відразу після зіткнення становить

\ begin {рівняння} E_ {a} ^ {m e c h} =\ frac {1} {2} I_ {S}\ омега_ {a} ^ {2} +\ frac {1} m_ {1}\ ліво (v_ {i}/2\ праворуч) ^ {2}\ кінець {рівняння}

Використовуючи наші результати для моменту інерції\(I_{S}\) (Рівняння (19.5.39)) та\(\omega_{2}\) (Рівняння (19.5.40)), ми маємо це

\ begin {рівняння} E_ {a} ^ {\ текст {мехе}} =\ фракція {1} {2} (1/3) m_ {2} l^ {2}\ ліворуч (\ frac {3 m_ {1} v_ {i}}} {2} l}\ праворуч) ^ {2} +\ frac {1} {2} m_ {1}\ ліворуч (v_ {i}/2\ праворуч) ^ {2} =\ розриву {3 м_ {1} ^ {2} v_ {i} ^ {2}} {8 m_ {2}} +\ frac {1} m_ {1}\ ліворуч (v_ {i}/2\ праворуч) ^ {2}\ кінець {рівняння}

Механічна енергія, коли стрижень тільки досягає стелі, коли кінцева кутова швидкість дорівнює нулю, тоді

\ begin {рівняння} E_ {f} ^ {m e c h} =m_ {2} g (л/2) +\ frac {1} {2} m_ {1}\ left (v_ {i}/2\ праворуч) ^ {2}\ end {рівняння}

Тоді умова, що механічна енергія постійна, стає

\ begin {рівняння}\ гідророзриву {3 м_ {1} ^ {2} v_ {i} ^ {2}} {8 м_ {2}} +\ гідророзриву {1} m_ {1}\ ліворуч (v_ {i}/2}} ^ {2} =m_ {2} g (l/2) +\ frac {1} {2} {2} m_ 1}\ ліворуч (v_ {i}/2\ праворуч) ^ {2}\ end {рівняння}

Тепер ми можемо вирішити рівняння (19.5.42) для початкової швидкості об'єкта

\ begin {рівняння} v_ {i} =\ frac {m_ {2}} {m_ {1}}\ sqrt {\ frac {4 г л} {3}}\ кінець {рівняння}

Тепер повернемося до переходу зі стану i в стан a. і визначимо обмеження на коефіцієнт маси для того, щоб зіткнення було пружним. Механічна енергія перед зіткненням

\ begin {рівняння} E_ {i} ^ {m e c h} =\ frac {1} {2} m_ {1} v_ {i} ^ {2}\ end {рівняння}

Якщо ми накладемо умову, що зіткнення еластичне, то

\ begin {рівняння} E_ {i} ^ {m e c h} =E_ {a} ^ {m e c h}\ end {рівняння}

Заміна рівнянь (19.5.41) та (19.5.44) на рівняння (19.5.45) дає

\ begin {рівняння}\ гідророзриву {1} {2} m_ {1} v_ {i} ^ {2} =\ гідророзриву {3 м_ {1} ^ {2} v_ {2}} {8 m_ {2}} +\ frac {1} m_ {1}\ ліворуч (v_ {i}/2\ праворуч) ^ {2}\ кінець {рівняння}

Це спрощує

\ begin {рівняння}\ гідророзриву {3} {8} m_ {1} v_ {i} ^ {2} =\ гідророзриву {3 m_ {1} ^ {2} v_ {i} ^ {2}} {8 m_ {2}}\ end {рівняння}

Отже, ми можемо вирішити для співвідношення маси, необхідне для забезпечення еластичності зіткнення, якщо кінцева швидкість об'єкта становить половину, то початкова швидкість.

\ begin {рівняння}\ гідророзриву {m_ {2}} {m_ {1}} =1\ end {рівняння}

Зверніть увагу, що це співвідношення маси не залежить від початкової швидкості об'єкта.