17.3: Крутний момент

Визначення крутного моменту навколо точки

Для того, щоб зрозуміти динаміку обертового жорсткого тіла, ми введемо нову величину - крутний момент. Нехай сила\(\overrightarrow{\mathbf{F}}_{P}\) з величиною\(F=\left|\overrightarrow{\mathbf{F}}_{P}\right|\) діяти в точці P\(\overrightarrow{\mathbf{r}}_{S, P}\) Дозволяти вектор від точки\(S\) до точки P, з величиною\(r=\left|\overrightarrow{\mathbf{r}}_{S, P}\right|\). Кут між векторами\(\overrightarrow{\mathbf{r}}_{S, P}\) і\(\overrightarrow{\mathbf{F}}_{p}\) дорівнює θ с\([0 \leq \theta \leq \pi]\) (рис. 17.9).

Малюнок 17.9 Крутний момент близько точки\(S\) за рахунок сили, що діє в точці Р

Крутний момент навколо точки,\(S\) обумовлений силою, що\(\overrightarrow{\mathbf{F}}_{P}\) діє при Р, визначається

\[\vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, P} \times \overrightarrow{\mathbf{F}}_{P} \nonumber \]

Величина крутного моменту близько точки\(S\) за рахунок сили, що\(\overrightarrow{\mathbf{F}}_{P}\) діє при Р, задається

\[\tau_{S} \equiv\left|\vec{\tau}_{S}\right|=r F \sin \theta \nonumber \]

Одиницями СІ для крутного моменту є [Н⋅м]. Напрямок крутного моменту перпендикулярно площині, утвореній векторами\(\overrightarrow{\mathbf{r}}_{S, P}\) і\(\overrightarrow{\mathbf{F}}_{P} \quad \text { (for } \left.[0<\theta<\pi]\right)\), а за визначенням вказує в напрямку вектора одиниці нормалі до площини,\(\hat{\mathbf{n}}_{R H R}\) як показано на малюнку 17.10.

Малюнок 17.10 Векторний напрямок крутного моменту

На малюнку 17.11 показані два різних способи визначення висоти та основи для паралелограма, визначеного векторами\(\overrightarrow{\mathbf{r}}_{S, P} \text { and } \overrightarrow{mathbf{F}}_{P}\).

Малюнок 17.11 Площа крутного моменту паралелограма.

\(r_{\perp}=r \sin \theta\)\(F_{\perp}=F \sin \theta\)Дозволяти і бути складовою сили\(\overrightarrow{\mathbf{F}}_{P}\), яка перпендикулярна лінії, що проходить від точки\(S\) до Р. (Нагадаємо, кут θ має діапазон значень\(0 \leq \theta \leq \pi\) так обидва\(r_{\perp} \geq 0 \text { and } F_{\perp} \geq 0\). Тоді площа паралелограма,\(\overrightarrow{\mathbf{r}}_{S, P}\) визначена і\(\overrightarrow{\mathbf{F}}_{P}\), задається

\[\text { Area }=\tau_{S}=r_{\perp} F=r F_{\perp}=r F \sin \theta \nonumber \]

Ми можемо інтерпретувати кількість\(r_{\perp}\) наступним чином.

Малюнок 17.12 Момент плеча про точку\(S\) і лінію дії сили, що проходить через точку Р

Починаємо з малювання лінії дії сили\(\overrightarrow{\mathbf{F}}_{P}\). Це пряма лінія, що проходить через Р, паралельна напрямку сили\(\overrightarrow{\mathbf{F}}_{P}\). Намалюйте перпендикуляр до цієї лінії дії, яка проходить через точку\(S\) (рис. 17.12). Довжина цього перпендикуляра\(r_{\perp}=r \sin \theta\), називається моментом плеча\(S\) про точку сили\(\overrightarrow{\mathbf{F}}_{P}\).

Слід мати на увазі три важливі властивості крутного моменту:

1. Крутний момент дорівнює нулю, якщо вектори\(\overrightarrow{\mathbf{r}}_{S, P}\) і\(\overrightarrow{\mathbf{F}}_{P}\) паралельні (θ = 0) або антипаралельні\((\theta=\pi)\).

2. Крутний момент - вектор, напрямок і величина якого залежать від вибору точки,\(S\) про яку розраховується крутний момент.

3. Напрямок крутного моменту перпендикулярно площині, утвореній двома векторами,\(\overrightarrow{\mathbf{F}}_{P}\) і\(r=\left|\overrightarrow{\mathbf{r}}_{S, P}\right|\) (вектор від точки\(S\) до точки Р).

Альтернативний підхід до присвоєння знаку конвенції для крутного моменту

У разі, коли всі вектори сил\(\overrightarrow{\mathbf{F}}_{i}\) і положення\(\overrightarrow{\mathbf{r}}_{i, P}\) є копланарними (або нульовими), ми можемо замість того, щоб посилатися на напрямок крутного моменту, призначити суто алгебраїчний позитивний або негативний знак крутного моменту відповідно до наступної конвенції. Відзначимо, що дуга на малюнку 17.13а кружляє в напрямку проти годинникової стрілки. (Рисунки 17.13a і 17.13b використовують спрощення припущення, тільки для цілей малюнка, що два вектори, про які йдеться,\(\overrightarrow{\mathbf{F}}_{P}\) і\(\overrightarrow{\mathbf{r}}_{S, P}\) перпендикулярні. Точка,\(S\) про яку обчислюються крутні моменти, не показана.)

Малюнок 17.13 (a) Позитивний крутний момент поза площиною, (b) позитивний крутний момент у площину

Ми можемо пов'язати з цією орієнтацією проти годинникової стрілки одиничний нормальний вектор\(\hat{\mathbf{n}}\) відповідно до правилом правої руки: скрутіть пальці правої руки в напрямку проти годинникової стрілки, а великий палець правої руки потім вкаже у\(\hat{\mathbf{n}}_{1}\) напрямку (рис. 17.13а). Дуга на малюнку 17.13b кружляє за годинниковою стрілкою, і ми пов'язуємо цю орієнтацію з одиницею нормалі\(\hat{\mathbf{n}}_{2}\).

Важливо зазначити, що терміни «за годинниковою стрілкою» та «проти годинникової стрілки» можуть відрізнятися для різних спостерігачів. Наприклад, якщо площина, що містить\(\overrightarrow{\mathbf{F}}_{P} \text { and } \overrightarrow{\mathbf{r}}_{S, P}\), горизонтальна, спостерігач над площиною і спостерігач нижче площини не погодиться з двома термінами. Для вертикальної площини напрямки, які два спостерігачі з протилежних сторін площини були б дзеркальними відображеннями один одного, і тому знову спостерігачі не погодилися б.

1. Припустимо, ми вибираємо проти годинникової стрілки як позитивні. Потім призначаємо позитивний знак для складової крутного моменту, коли крутний момент знаходиться в тому ж напрямку, що і одиниця нормального\(\hat{\mathbf{n}}_{1}, \text { i.e. } \vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, P} \times \overrightarrow{\mathbf{F}}_{P}=+\left|\overrightarrow{\mathbf{r}}_{S, P}\right|\left|\overrightarrow{\mathbf{F}}_{P}\right| \hat{\mathbf{n}}_{l}\) (рис. 17.13а).

2. Припустимо, ми вибираємо за годинниковою стрілкою Потім привласнюємо негативний знак для складової крутного моменту на малюнку 17.13б тому, що крутний момент спрямований навпроти одиниці нормального\(\hat{\mathbf{n}}_{2}, \text { i.e. } \vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, P} \times \overrightarrow{\mathbf{F}}_{P}=-\left|\overrightarrow{\mathbf{r}}_{S, P}\right| \overrightarrow{\mathbf{F}}_{P} \mid \hat{\mathbf{n}}_{2}\).

Приклад 17.6 Крутний момент і векторний добуток

Розглянемо два вектори\(\overrightarrow{\mathbf{r}}_{P, F}=x \hat{\mathbf{i}}\) з\(x>0\) і\(\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}+F_{z} \hat{\mathbf{k}}\) з\(F_{x}>0 \text { and } F_{z}>0\) Обчислити крутний момент\(\overrightarrow{\mathbf{r}}_{P, F} \times \overrightarrow{\mathbf{F}}\).

Рішення: Обчислюємо векторний добуток, зазначивши, що при правильному виборі одиничних векторів,\(\hat{\mathbf{i}} \times \hat{\mathbf{i}}=\overrightarrow{\mathbf{0}} \text { and } \hat{\mathbf{i}} \times \hat{\mathbf{k}}=-\hat{\mathbf{j}}\)

\[\overrightarrow{\mathbf{r}}_{P, F} \times \overrightarrow{\mathbf{F}}=x \hat{\mathbf{i}} \times\left(F_{x} \hat{\mathbf{i}}+F_{z} \hat{\mathbf{k}}\right)=\left(x \hat{\mathbf{i}} \times F_{x} \hat{\mathbf{i}}\right)+\left(x \hat{\mathbf{i}} \times F_{z} \hat{\mathbf{k}}\right)=-x F_{z} \hat{\mathbf{j}} \nonumber \]

Тому\(x>0 \text { and } F_{z}>0\) що напрямок векторного добутку знаходиться в негативному y - напрямку.

Приклад 17.7 Розрахунок крутного моменту

На малюнку 17.14 до одного кінця важеля довжиною L прикладається сила величини F. Яка величина і напрямок крутного моменту навколо точки S?

Малюнок 17.15 Система координат

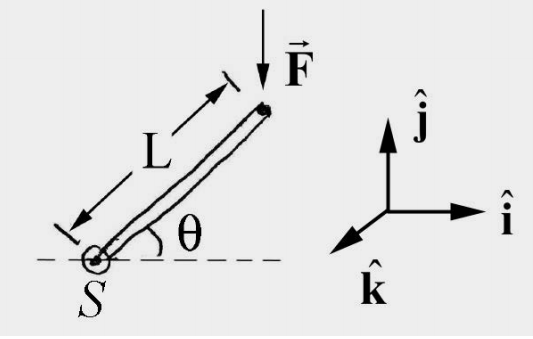
Рішення: Оберіть вектори одиниць такої\(\hat{\mathbf{i}} \times \hat{\mathbf{j}}=\hat{\mathbf{k}}\), що,\(\hat{\mathbf{i}}\) вказуючи вправо і\(\hat{\mathbf{j}}\) спрямовуючи вгору (рис. 17.15). Крутний момент навколо точки\(S\) задається тим,\(\vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, F} \times \overrightarrow{\mathbf{F}}\) де\(\overrightarrow{\mathbf{r}}_{S F}=L \cos \theta \hat{\mathbf{i}}+L \sin \theta \hat{\mathbf{j}}\) і\(\overrightarrow{\mathbf{F}}=-F \hat{\mathbf{j}}\) далі

\[\vec{\tau}_{S}=(L \cos \theta \hat{\mathbf{i}}+L \sin \theta \hat{\mathbf{j}}) \times-F \hat{\mathbf{j}}=-F L \cos \theta \hat{\mathbf{k}} \nonumber \]

Приклад 17.8 Крутний момент і щиколотка

Людина маси m присідає з їх вагою рівномірно розподіленим на обох навшпиньках. Діаграма сили вільного тіла на скелетної частини стопи показана на малюнку 17.16. Нормальна сила\(\overrightarrow{\mathbf{N}}\) діє в місці контакту стопи і землі. У такому положенні великогомілкова кістка діє на стопу в точці\(S\) з силою\(\overrightarrow{\mathbf{F}}\) невідомої величини\(F=|\overrightarrow{\mathbf{F}}|\) і робить з\(\beta\) вертикаллю невідомий кут. Ця сила діє на щиколотку на горизонтальній відстані s від точки, де стопа контактує з підлогою. Ахіллове сухожилля також діє на стопу і знаходиться під значною напругою з величиною\(T \equiv|\overrightarrow{\mathbf{T}}|\) і діє під кутом α з горизонталлю, як показано на малюнку. Сухожилля діє на щиколотку на горизонтальній відстані b від точки,\(S\) де великогомілкова кістка впливає на стопу. Ви можете ігнорувати вагу стопи. Нехай g - гравітаційна константа. Обчислити крутний момент навколо точки\(S\) за рахунок (а) сухожилля сили на стопі; (б) сили великогомілкової кістки на стопі; (в) нормальної сили підлоги на стопі.

Малюнок 17.16 Діаграма сили та система координат для щиколотки

Рішення: (а) Спочатку розрахуємо крутний момент, обумовлений силою ахіллового сухожилля на щиколотці. Сила сухожилля має вектор розкладання\(\overrightarrow{\mathbf{T}}=T \cos \alpha \hat{\mathbf{i}}+T \sin \alpha \hat{\mathbf{j}}\)

Малюнок 17.17 Діаграма крутного моменту сили сухожилля на щиколотці Малюнок 17.18 Діаграма крутного моменту для нормальної сили на щиколо\(\overrightarrow{\mathbf{r}}_{S, N}\)

Вектор від точки\(S\) до точки дії сили задається\(\overrightarrow{\mathbf{r}}_{S, T}=-b \hat{\mathbf{i}}\) (рис. 17.17). Тому крутний момент, обумовлений силою сухожилля\(\overrightarrow{\mathbf{T}}\) на щиколотці про точку\(S\), тоді

\[\vec{\tau}_{S, T}=\overrightarrow{\mathbf{r}}_{S, T} \times \overrightarrow{\mathbf{T}}=-b \hat{\mathbf{i}} \times(T \cos \alpha \hat{\mathbf{i}}+T \sin \alpha \hat{\mathbf{j}})=-b T \sin \alpha \hat{\mathbf{k}} \nonumber \]

(б) Діаграма крутного моменту для нормальної сили показана на малюнку 17.18. Вектор від точки\(S\) до точки, де на стопу діє нормальна сила\(\overrightarrow{\mathbf{r}}_{S, N}=(\hat{\mathbf{i}}-h \hat{\mathbf{j}})\). Оскільки вага рівномірно розподіляється на дві ноги, нормальна сила на одній нозі дорівнює половині ваги, або\(N=(1 / 2) m g\). Тому нормальна сила дається\(\overrightarrow{\mathbf{N}}=N \hat{\mathbf{j}}=(1 / 2) m g \hat{\mathbf{j}}\). Тому крутний момент нормальної сили про точку\(S\) дорівнює

\[\vec{\tau}_{S, N}=\overrightarrow{\mathbf{r}}_{S, N} \times N \hat{\mathbf{j}}=((\hat{\mathbf{i}}-h \hat{\mathbf{j}}) \times N \hat{\mathbf{j}}=s N \hat{\mathbf{k}}=(1 / 2) s m g \hat{\mathbf{k}} \nonumber \]

(c) Сила\(\overrightarrow{\mathbf{F}}\), яку великогомілкова кістка чинить на щиколотку, не внесе жодного внеску в крутний момент щодо цієї точки,\(S\) оскільки великогомілкова сила діє в точці,\(S\) а отже, і векторі\(\overrightarrow{\mathbf{r}}_{S, F}=\overrightarrow{\mathbf{0}}\).